Контрольная работа на тему Высшая математика 2
Работа добавлена на сайт bukvasha.net: 2014-07-03Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.
Предоплата всего
от 25%
Подписываем
договор
Контрольная работа
Высшая математика
ЗАДАЧА 1.
В декартовой прямоугольной системе координат даны вершины пирамиды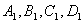 
.
Найдите:
а) длину ребра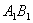 
;
б) косинус угла между векторами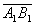 
и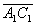 
;
в) уравнение ребра ;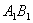
г) уравнение грани 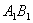С1; если А1 (-2,2,2),В1(1,-3.0), С1(6,2,4), D1(5,7,-1).
Решение.
а) Найдем координаты вектора А1В1 по формуле
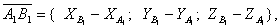
где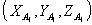 
- координаты точки А1,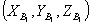 
-координаты точки В1.
Итак 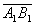={1-(-2);-3-2;0-2}={3;-5;-2}. Тогда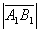 
= 
= 
.
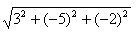
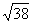
Итак, длина отрезка,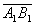 
(или длина векторе 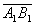) равна 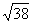. Это и есть искомая длина ребра.
б) Координаты 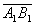={3;-5;-2} уже известны, осталось определить координаты вектора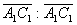 
={6- (-2); 2 - 2; 4 - 2}= {8,0; 2}.
Угол между векторами 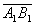и 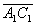вычислим по формуле
cos φ = (А1В1, А1С1)
|А1В1|·| А1С1|
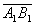
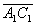
где скалярое произведение векторов А1В1 и А1С1 равно ( , )=3·8+(-5)·0+(-2)=24+0-4=20,
| |= , | |= 
= 
.
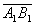
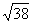
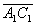
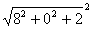
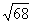
Итак, cos φ = 20 = 10
· 
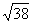
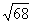
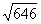
в) Координаты точки А1(-2,2,2) обозначим соответственно Х0 = -2, У0 = 2, Z0 = 2, а координаты точки В1(1,-3,0) через X1 = 1, У1 = -3, Z1 = 0 и воспользуемся уравнением прямой и пространстве, проходящей через две точки:
.
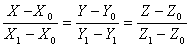
Следовательно, уравнение ребра 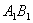имеет вид
.
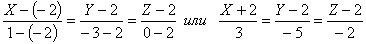
г) Обозначим координаты векторов 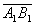, и 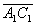через Х1=3, У1= -5, Z1= -2 и Х2=8, У2= 0, Z2=2 соответственно. Векторное произведение данных векторов определяется формулой
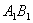
·A1C1 = {Y1·Z2-Y2·Z1;Z1·X2-Z2·X1;X1·Y2-X2·Y2} =
= {(-5)·2-0·(-2);-2·8-2·3;3·0-8·(-5)}={-10,-22,40}
Так как данный вектор перпендикулярен грани 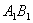С1, то можно воспользоваться уравнением плоскости, проходящей через точку (Х0 У0, Z0) перпендикулярно вектору {А;В;С}, которое имеет вид A·(X-X0)+B·(Y-Y0)+С·(Z-Z0)=0.
Подставим координаты точки А1 (Хо= -2, У0=2, Z0=2) и координаты перпендикулярного вектора А= -10, В= -22, С=40 в это уравнение:
- 10 ( X + 2 ) - 22 (У – 2) т 40 ( Z- 2) - 0. Раскроем скобки и приведем подобные члены - 10 х -22 у + 40z + (-20 + 44-80)=0. Итак, уравнение грани 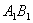,C1 имеет вид: -10х- 22у + 4О z-56=0 или -5х- lly + 20z-28=0.
ЗАДАЧА 2.
Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
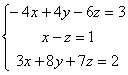
Решение.
а) Решим данную систему уравнений с помощью формул Крамера (см.[2] глава 10. стр. 268). Рассмотрим произвольную систему трех линейных уравнений с тремя неизвестными:
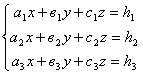
Решение.
а) Решим данную систему уравнений с помощью формул Крамера ( см. [2] глава 10, стр. 268).
Тогда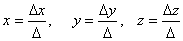 
, где
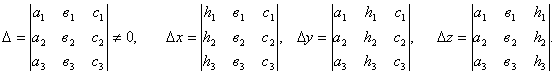
Так как Δx= -60; Δy= -60; Δz=60; Δ= -120, то x=
6) решим данную систему уравнений методом Гаусса. Метод Гаусса состоит в том, что с помощью элементарных преобразований система уравнении приводится к равносильной системе ступенчатого (или треугольного) вида из которой последовательно, начиная с последнего уравнения, легко находят все неизвестные системы.
Составим расширенную матрицу данной системы.
Поменяем местами первую и вторую строки матрицы, чтобы в ее левом верхнем углу была единица. Получим матрицу.
Умножим каждый элемент первой строки матрицы на 4 и прибавим полученные числа к соответствующим элементам второй строки. Матрица примет вид.
=
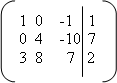
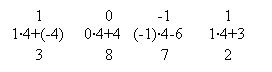
Умножим каждый элемент первой строки матрицы на -3. и прибавим полученные числа к соответствующим элементам третьей строки. Получим:
=
Разделим каждый элемент второй строки матрицы на 4, чтобы второй элемент, стоящий на главной диагонали матрицы, стал равным 1.
Умножим каждый элемент второй строки матрицы на -8 и прибавим полученные числа к соответствующим элементам третьей строки:
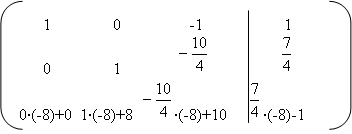
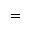
Данная матрица соответствует системе уравнений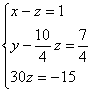 
, решение которой совпадает с решением исходной системы. Начинай с последнего уравнения, несложно найти все неизвестные.
Действительно, так как z=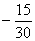 
= 
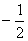
и y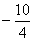 
z=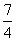 
, то y ·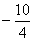
Отсюда, y -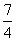 
= 
= 
= 
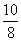
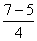
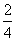
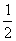
. Из x-z=1 имеем =z+1= 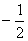+1=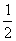
Ответ: x= 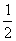, y= 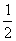, z= .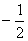
Элементы теории вероятности и математической статистики
Для решения задачи 3 см. [5] глава 1. § 1—5.
ЗАДАЧА 3.
На складе университета хранится 28 одинаковых упаковок писчей бумаги. Известно, что в четырех из них содержится бумага более низкого качества. Случайным образом выбирают три упаковки бумаги, Вычислить вероятность того, что среди них;
А) нет упаковок с бумагой более низкого качества,
Б) есть одна упаковка такой бумаги.
Решение. Общее число возможных элементарных исходов для данных испытаний равно числу способов, которыми можно извлечь 3 упаковки бумаги из 28 упаковок, то есть
= 
= 
= 
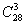
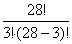
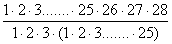
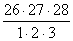
=13·9·28=3276 – числу сочетаний из 28 элементов по 3.
а) Подсчитаем число исходов, благоприятствующих интересующему нас событию (нет упаковок с бумагой более низкого качества). Это число исходов ровно числу способов, которыми можно извлечь 3 упаковки бумаги из 24 упаковок (столько упаковок содержит бумагу высшего сорта), то есть
= 
= 
= 
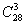
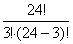
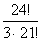
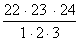
=11·23·8=2024
искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
P1=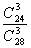 
= 
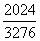
≈0,62
б) Подсчитаем число исходов, благоприятствующих данному событию (среди трех упаковок бумаги ровно 1 упаковка содержит бумагу более низкого качества): две упаковки можно выбрать из 24 упаковок: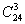 
= 
= 
= 
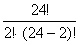
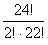
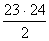
=276 способами, при этом одну упаковку нужно выбирать из четырех: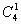 
= 
= 
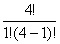
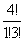
=4 способами. Следовательно, число благоприятствующих исходов равно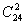 
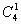
· =276·4=1104
Искомая вероятность равна отношению числа исходов, благоприятствующих данному событию, к числу всех элементарных исходов p2=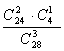 
= 
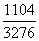
≈0,34
Ответ: а) p1 =0,62; б) р2 =0,34.
ЗАДАЧА 4.
Магазин получает электролампочки с двух заводов, причем доля первого завода составляет 25 %. Известно, что доля брака на этих заводах равна соответственно 5 % и 10 % от всей выпускаемой продукции. Продавец наугад берет одну лампочку. Какова вероятность того, что она окажется бракованной?
Решение: Обозначим через А событие - «лампочка окажется бракованной». Возможны следующие гипотезы о происхождении этой лампочки: H1-лампочка поступила с первого завода, H2-лампочка поступила со второго завода. Так как доля первого завода составляет 25 %, то вероятности этих гипотез равны соответственно p(H1)=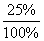 
=0,25; p(H2)=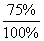 
=0,75.
Условная вероятность того, что бракованная лампочка выпущена первым заводом – p(A/H1)=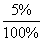 
=0,05, вторым заводом - p(A/H2)=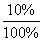 
=0,10 искомую вероятность того, что продавец взял бракованную лампочку, находим по формуле полной вероятности
р(А) = P(H1)· p(A/H1)+P(H2)·(A/H2)=0,25·0,05+0,75·0,10=0,0125+0,075=0.0875
Ответ: р(А) = 0,0875.
Для решения задачи 5 см. [5]глава 6 § 1—3, глава 7 § 1-2, глава 8 § J—3.
ЗАДАЧА 5.
Задан закон распределения дискретной случайной величены X:
Найти:
а) неизвестную вероятность р.
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение σ данной случайной величены;
Решение:
а) так как сумма всех, вероятностей должна равняться единице, то получим уравнение
0,05-p + 0,12 + 0,23-0,32 + 0,14+0,04 = 1.
Отсюда р+0,9 = 1 и р=0,1.
б) Математическое ожидание М это сумма всех произведений значений случайной величины на их вероятности:
М = (-4)·0,05+(-2)·0,1 + 0·0,12 + 2·0,23 + 4·0,32 + 6·0,14 + +8·0,04-0,2-0,2+0 + 0,46 + 1,28 + 0,84 + 0.32 = -0,4 + 2,9 = 2,5.
Дисперсия D=∑(x1)2·p1-M2=
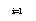
=(-4)·0.05+(-2)2·0,1+02·0,12+22·0,23+42·0,32+62·0,14+82·0,04-(2,5)2=
=0,8+0+0,92+5,12+5,04+2,56-6,25=8,59
Среднее квадратическое отклонение σ =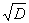 
= 
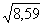
≈2,9
ЗАДАЧА 6.
Построить выпуклый многоугольник, заданный системой неравенств
x1-x2 ≥ - 2;
x1-3x2 ≥ - 10,
x1+2 x2 ≥4,
x1 ≤8,
x2≥0.
Пользуясь геометрической интерпретацией основной задачи линейного программирования, найти минимум и максимум линейной формы
L=2x1+x2
Решение. Построим прямоугольную систему координат x1Ox2. Если в этой системе построить прямую ax1 + bx2 = c, то она разобьет плоскость x1Ох2 на две полуплоскости, каждая из которых лежит но одну сторону от прямой. Сама прямая в этом случае называется граничной и принадлежит обеим полуплоскостям. Координаты точек, лежащих в одной полуплоскости, удовлетворяют неравенству ах1+bx2≤c, а координаты точек, лежащих в другой полуплоскости,— неравенству. ах1+bx2≥c. Построим в плоскости x1Ox2 граничные прямые x1-x2=-2(AB), x1-3x2=-10(BC), x1+2 x2=4(AE), x1=8(CD) и x2=0(ED).
В результате получим пятиугольник ABCDE (рис. 12). Значения x1 и x2, удовлетворяющие системе неравенств (1), являются координатами точек, лежащих внутри или на границе найденного пятиугольника.
Теперь задача сводится к тому, чтобы найти те значения x1 и x2, при которых линейная форма, L (2) имеет минимум, и те значения x1 и х2, при которых линейная форма L достигает максимума. Из рис. 1 видно, что координаты всех точек, лежащих внутри или на границе пятиугольника, не являются отрицательными, т. е. все значения x1 и х2 больше или равны нулю. Для каждой точки плоскости x1Ox2 линейная форма L принимает фиксированное значение. Множество точек, при которых линейная форма L принимает значение L1, есть прямая 2x1+х2=L1(l1), которая перпендикулярна вектору N = 2i+j. Если прямую l1 передвигать параллельно самой себе в положительном направлении вектора N, то линейная форма L будет возрастать, а если прямую передвигать в противоположном направлении — убывать. Построим прямую (l1) для того случая, когда L = 0, т.е. построим прямую 2x1+х2=0. Как видно из рис. 1 , при передвижении прямой l1 в положительном направлении вектора N она впервые встретится с вершиной А построенного пятиугольника ABCDE. В этой вершине линейная форма L имеет минимум. Следовательно, Lmin=2·0+1·2=2, При дальнейшем передвижении прямой l1 параллельно самой себе в положительном направлении вектора N значение линейной формы L будет возрастать, и оно достигнет максимального значения в точке С(8; 6). Таким образом, Lmax=2·8+1·6=22.
Высшая математика
ЗАДАЧА 1.
В декартовой прямоугольной системе координат даны вершины пирамиды
Найдите:
а) длину ребра
б) косинус угла между векторами
в) уравнение ребра
г) уравнение грани
Решение.
а) Найдем координаты вектора А1В1 по формуле Итак
Итак, длина отрезка,
б) Координаты
Угол между векторами
cos φ = (А1В1, А1С1) |А1В1|·| А1С1| где скалярое произведение векторов А1В1 и А1С1 равно (|
Итак, cos φ = 20 = 10 в) Координаты точки А1(-2,2,2) обозначим соответственно Х0 = -2, У0 = 2, Z0 = 2, а координаты точки В1(1,-3,0) через X1 = 1, У1 = -3, Z1 = 0 и воспользуемся уравнением прямой и пространстве, проходящей через две точки:
Следовательно, уравнение ребра
г) Обозначим координаты векторов
= {(-5)·2-0·(-2);-2·8-2·3;3·0-8·(-5)}={-10,-22,40}
Так как данный вектор перпендикулярен грани
Подставим координаты точки А1 (Хо= -2, У0=2, Z0=2) и координаты перпендикулярного вектора А= -10, В= -22, С=40 в это уравнение:
- 10 ( X + 2 ) - 22 (У – 2) т 40 ( Z- 2) - 0. Раскроем скобки и приведем подобные члены - 10 х -22 у + 40z + (-20 + 44-80)=0. Итак, уравнение грани
ЗАДАЧА 2.
Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
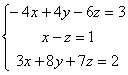
Решение.
а) Решим данную систему уравнений с помощью формул Крамера (см.[2] глава 10. стр. 268). Рассмотрим произвольную систему трех линейных уравнений с тремя неизвестными:
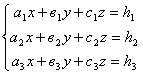
Решение.
а) Решим данную систему уравнений с помощью формул Крамера ( см. [2] глава 10, стр. 268).
Тогда
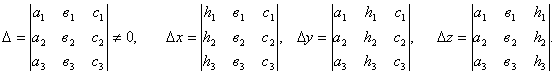
Так как Δx= -60; Δy= -60; Δz=60; Δ= -120, то x= 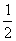; y= 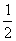; z= .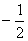
6) решим данную систему уравнений методом Гаусса. Метод Гаусса состоит в том, что с помощью элементарных преобразований система уравнении приводится к равносильной системе ступенчатого (или треугольного) вида из которой последовательно, начиная с последнего уравнения, легко находят все неизвестные системы. Составим расширенную матрицу данной системы.
| -4 4 -6 3 1 0 -1 1 3 8 7 2 |
Поменяем местами первую и вторую строки матрицы, чтобы в ее левом верхнем углу была единица. Получим матрицу.
| 1 0 -1 1 -4 4 -6 3 3 8 7 2 |
Умножим каждый элемент первой строки матрицы на 4 и прибавим полученные числа к соответствующим элементам второй строки. Матрица примет вид.
| 1 0 -1 1 0 4 -10 7 3 8 7 2 |
| 1 0 -1 1 1·4+(-4) 0·4+4 (-1)·4-6 1·4+3 3 8 7 2 |
=
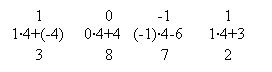
Умножим каждый элемент первой строки матрицы на -3. и прибавим полученные числа к соответствующим элементам третьей строки. Получим:
| 1 0 -1 1 0 4 -10 7 0 8 10 -1 |
| 1 0 -1 1 0 4 -10 7 1·(-3)+3 0·(-3)+8 (-1)·(-3)+7 1·(-3)+2 |
=
Разделим каждый элемент второй строки матрицы на 4, чтобы второй элемент, стоящий на главной диагонали матрицы, стал равным 1.
| 1 0 -1 1 0 1 0 8 10 -1 |
Умножим каждый элемент второй строки матрицы на -8 и прибавим полученные числа к соответствующим элементам третьей строки:
| 1 0 -1 1 0 1 0·(-8)+0 1·(-8)+8 |
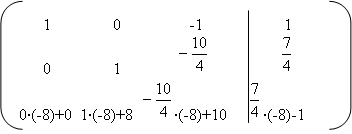
| 1 0 -1 1 0 1 0 0 30 -15 |
| = |
Данная матрица соответствует системе уравнений
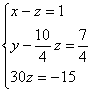
Действительно, так как z=
Отсюда, y
Ответ: x=
Элементы теории вероятности и математической статистики
Для решения задачи 3 см. [5] глава 1. § 1—5.
ЗАДАЧА 3.
На складе университета хранится 28 одинаковых упаковок писчей бумаги. Известно, что в четырех из них содержится бумага более низкого качества. Случайным образом выбирают три упаковки бумаги, Вычислить вероятность того, что среди них;
А) нет упаковок с бумагой более низкого качества,
Б) есть одна упаковка такой бумаги.
Решение. Общее число возможных элементарных исходов для данных испытаний равно числу способов, которыми можно извлечь 3 упаковки бумаги из 28 упаковок, то есть
а) Подсчитаем число исходов, благоприятствующих интересующему нас событию (нет упаковок с бумагой более низкого качества). Это число исходов ровно числу способов, которыми можно извлечь 3 упаковки бумаги из 24 упаковок (столько упаковок содержит бумагу высшего сорта), то есть
искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
P1=
б) Подсчитаем число исходов, благоприятствующих данному событию (среди трех упаковок бумаги ровно 1 упаковка содержит бумагу более низкого качества): две упаковки можно выбрать из 24 упаковок:
Искомая вероятность равна отношению числа исходов, благоприятствующих данному событию, к числу всех элементарных исходов p2=
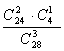
Ответ: а) p1 =0,62; б) р2 =0,34.
ЗАДАЧА 4.
Магазин получает электролампочки с двух заводов, причем доля первого завода составляет 25 %. Известно, что доля брака на этих заводах равна соответственно 5 % и 10 % от всей выпускаемой продукции. Продавец наугад берет одну лампочку. Какова вероятность того, что она окажется бракованной?
Решение: Обозначим через А событие - «лампочка окажется бракованной». Возможны следующие гипотезы о происхождении этой лампочки: H1-лампочка поступила с первого завода, H2-лампочка поступила со второго завода. Так как доля первого завода составляет 25 %, то вероятности этих гипотез равны соответственно p(H1)=
Условная вероятность того, что бракованная лампочка выпущена первым заводом – p(A/H1)=
р(А) = P(H1)· p(A/H1)+P(H2)·(A/H2)=0,25·0,05+0,75·0,10=0,0125+0,075=0.0875
Ответ: р(А) = 0,0875.
Для решения задачи 5 см. [5]глава 6 § 1—3, глава 7 § 1-2, глава 8 § J—3.
ЗАДАЧА 5.
Задан закон распределения дискретной случайной величены X:
|
а) неизвестную вероятность р.
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение σ данной случайной величены;
Решение:
а) так как сумма всех, вероятностей должна равняться единице, то получим уравнение
0,05-p + 0,12 + 0,23-0,32 + 0,14+0,04 = 1.
Отсюда р+0,9 = 1 и р=0,1.
б) Математическое ожидание М это сумма всех произведений значений случайной величины на их вероятности:
М = (-4)·0,05+(-2)·0,1 + 0·0,12 + 2·0,23 + 4·0,32 + 6·0,14 + +8·0,04-0,2-0,2+0 + 0,46 + 1,28 + 0,84 + 0.32 = -0,4 + 2,9 = 2,5.
| 7 |
Дисперсия D=∑(x1)2·p1-M2= | i=1 |
=(-4)·0.05+(-2)2·0,1+02·0,12+22·0,23+42·0,32+62·0,14+82·0,04-(2,5)2=
=0,8+0+0,92+5,12+5,04+2,56-6,25=8,59
Среднее квадратическое отклонение σ =
ЗАДАЧА 6.
Построить выпуклый многоугольник, заданный системой неравенств
x1-x2 ≥ - 2; x1-3x2 ≥ - 10,
x1+2 x2 ≥4,
x1 ≤8,
x2≥0.
Пользуясь геометрической интерпретацией основной задачи линейного программирования, найти минимум и максимум линейной формы
L=2x1+x2
Решение. Построим прямоугольную систему координат x1Ox2. Если в этой системе построить прямую ax1 + bx2 = c, то она разобьет плоскость x1Ох2 на две полуплоскости, каждая из которых лежит но одну сторону от прямой. Сама прямая в этом случае называется граничной и принадлежит обеим полуплоскостям. Координаты точек, лежащих в одной полуплоскости, удовлетворяют неравенству ах1+bx2≤c, а координаты точек, лежащих в другой полуплоскости,— неравенству. ах1+bx2≥c. Построим в плоскости x1Ox2 граничные прямые x1-x2=-2(AB), x1-3x2=-10(BC), x1+2 x2=4(AE), x1=8(CD) и x2=0(ED).
В результате получим пятиугольник ABCDE (рис. 12). Значения x1 и x2, удовлетворяющие системе неравенств (1), являются координатами точек, лежащих внутри или на границе найденного пятиугольника.
| x2 |
  |
| E |
| D х1 |
 0 |
| Рис. 1 |
Теперь задача сводится к тому, чтобы найти те значения x1 и x2, при которых линейная форма, L (2) имеет минимум, и те значения x1 и х2, при которых линейная форма L достигает максимума. Из рис. 1 видно, что координаты всех точек, лежащих внутри или на границе пятиугольника, не являются отрицательными, т. е. все значения x1 и х2 больше или равны нулю. Для каждой точки плоскости x1Ox2 линейная форма L принимает фиксированное значение. Множество точек, при которых линейная форма L принимает значение L1, есть прямая 2x1+х2=L1(l1), которая перпендикулярна вектору N = 2i+j. Если прямую l1 передвигать параллельно самой себе в положительном направлении вектора N, то линейная форма L будет возрастать, а если прямую передвигать в противоположном направлении — убывать. Построим прямую (l1) для того случая, когда L = 0, т.е. построим прямую 2x1+х2=0. Как видно из рис. 1 , при передвижении прямой l1 в положительном направлении вектора N она впервые встретится с вершиной А построенного пятиугольника ABCDE. В этой вершине линейная форма L имеет минимум. Следовательно, Lmin=2·0+1·2=2, При дальнейшем передвижении прямой l1 параллельно самой себе в положительном направлении вектора N значение линейной формы L будет возрастать, и оно достигнет максимального значения в точке С(8; 6). Таким образом, Lmax=2·8+1·6=22. 