Контрольная работа на тему Прикладне вживання методів дискретної математики
Работа добавлена на сайт bukvasha.net: 2014-11-20Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ
Бердичівський політехнічний коледж
Контрольна робота
Прикладне вживання методів дискретної математики
м. Бердичів 2007 р.
Задача 2
Задача 3
Задача 4
Список використаної літератури
1. Задача 1
1. Задана універсальна множина U={a,b,c,d,e,f,g,h,i} і дві множини S={b,c,e,i}, T={c,e,f,i}. Знайти:
a) об’єднання, перетин, різницю і симетричну різницю множин S i T;
b) доповнення множини S і доповнення множини T;
c) прямий добуток множин S i T;
d) задати функцію із S в T: ін’єктивну, сюр’єктивну і бієктивну.
2. Дані відображення h1 і h2, що представляють множину сумісних кортежів. Знайти:
a) h3=(h1Èh2);
b) h4=(h1Çh2);
c) h5=(h12);
d) h6=(h1Dh2).
3. Хай дані відношення r1 і r2. Знайти:
a)
 r3=(r1Èr2);
r3=(r1Èr2);
b) r4=(r1Çr2);
c) r5=(r1\r2).
d) r6=(r1Dr2).
Відповідь:
1.
а) А = SÈT = {b, c, e, f, i};
А = SÇT = {c, e, i};
A = S\T = {b}; B = T\S = {f}:
A = SDT = {b, f}.
b) A = ùS = {a, d, f, g, h};
B = ùT = {a, b, d, g, h}.
c) SÄT = {{b, c}, {b, e}, {b, f}, {b, i}, {c, c}, {c, e}, {c, f}, {c, i}, {e, c}, {e, e}, {e, f}, {e, i}, {i, c}, {i, e}, {i, f}, {i, i}}.
2.
a) h3 =
b) h4 =
c) h5 =
d) h6 =
3.
a)
b)
c)
d)
2. Задача 2
У колоді 52 карти. У скількох випадках при виборі з колоди 10 карт серед них виявляться: а) рівно один туз; б) хоча б один туз; в) не менше двох тузів; г) рівно два тузи?
Відповідь:
а) Всього у колоді 4 тузи. Отже за правилом добутку перемножимо ймовірність вибору з чотирьох тузів одного туза та ймовірність вибору інших карт, тобто 9 з 48:
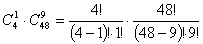
.
б) Хоча б один туз – це означає може бути і 4, і 3, і 2, і 1. Отже для розв'язку необхідно від ймовірності вибору 10 карт з 52 відняти ймовірність вибору 10 карт з 48:
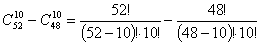
.
в) Не менше двох тузів – означає, що з 10 карт буде 4, 3 або 2 тузи. Рішенням буде попередня відповідь від якої відняти ймовірність вибору 1 туза (першої відповіді):
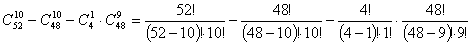
.
г) Аналогічно розв'язку першого завдання отримаєм:
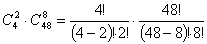
3. Задача 3
Граф заданий матрицею вагів. Побудувати для нього остов мінімальної ваги використовуючи алгоритми Пріма та Краскала, за алгоритмом Флойда обчислити найкоротші шляхи графа.

Відповідь:
Будова графа:
SHAPE \* MERGEFORMAT
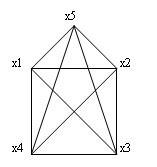
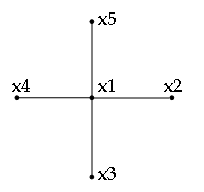
Побудова остову мінімальної ваги по алгоритму Краскала:
Встановлюємо частковий порядок по вазі ребер графа:
Будуємо остов мінімальної ваги:
SHAPE \* MERGEFORMAT
Обчислення найкоротших шляхів за алгоритмом Флойда:
Будуємо матрицю вагів та матрицю переходів:
А0 = 
Р0 = 
Елементи матриці вагів будемо знаходити за формулою:
Ak [i; j] = min (Ak-1 [i; j], Ak-1 [i; k] + Ak-1 [k; j])
Перша ітерація: k=1
А1 = 
Р1 = 
Друга ітерація: k=2
А2 = 
Р2 = 
Третя ітерація: k=3
А3 = 
Р3 = 
Четверта ітерація: k=4
А4 = 
Р4 = 
П’ята ітерація: k=5
А5 = 
Р5 = 
4. Задача 4
Знайти мінімальну ДНФ логічної функції F = F (хг, х2, х3, х4), яка дорівнює одиниці на наборах 2, 3, 4, 11, 14, 15 і нулю на решті наборів.
Відповідь:
Спочатку необхідно подати функцію у ДДНФ.
ДДНФ =x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4
Виконуємо склеювання:
1-2 x1x2x3
1-4 x2x3x4
2-4 x2x3x4
4-6 x1x3x4
5-6 x1x2x3
ДДНФ = x1x2x3 Ú x2x3x4 Ú x2x3x4 Ú x1x3x4 Ú x1x2x3 Ú x1x2x3x4
1-2 x2x3
1-3 x2x3
2-3 x2x3
3-4 x3x4
4-5 x1x3
ДДНФ = x2x3 Ú x3x4 Ú x1x3 Ú x1x2x3x4
Отже,
min ДНФ = x1x3 Ú x2x3 Ú x1x2x3x4
Список використаної літератури
1. «Дискретна математика» С.Лук’яненко. К-2000
2. «Комбінаторика» Д.Сафонов. М-1992
3. «Комбінаторика для програмістів» В.Липський. М-1988
4. Конспект лекцій
5. Комп’ютерна мережа Інтернет
Бердичівський політехнічний коледж
Контрольна робота
Прикладне вживання методів дискретної математики
м. Бердичів 2007 р.
Зміст
Задача 1Задача 2
Задача 3
Задача 4
Список використаної літератури
1. Задача 1
1. Задана універсальна множина U={a,b,c,d,e,f,g,h,i} і дві множини S={b,c,e,i}, T={c,e,f,i}. Знайти:
a) об’єднання, перетин, різницю і симетричну різницю множин S i T;
b) доповнення множини S і доповнення множини T;
c) прямий добуток множин S i T;
d) задати функцію із S в T: ін’єктивну, сюр’єктивну і бієктивну.
2. Дані відображення h1 і h2, що представляють множину сумісних кортежів. Знайти:
a) h3=(h1Èh2);
b) h4=(h1Çh2);
c) h5=(h12);
| h1 | у | x1 | x2 | x3 | h2 | у | x1 | x2 | x3 | |
| 2 | b | e | 6 | 3 | с | e | 6 | |||
| 3 | с | e | 5 | 5 | с | b | 2 | |||
| 5 | с | b | 2 | 4 | а | c | 5 | |||
| 4 | а | e | 5 | 2 | b | e | 6 |
3. Хай дані відношення r1 і r2. Знайти:
a)
| |
 r3=(r1Èr2);
r3=(r1Èr2); b) r4=(r1Çr2);
c) r5=(r1\r2).
d) r6=(r1Dr2).
| r1 | x1 | x2 | x3 | x4 | r2 | x1 | x2 | x3 | x4 | |
| x1 | 1 | 1 | 0 | 1 | x1 | 1 | 1 | 0 | 1 | |
| x2 | 0 | 1 | 0 | 1 | x2 | 1 | 1 | 0 | 0 | |
| x3 | 1 | 0 | 1 | 0 | x3 | 0 | 1 | 0 | 0 | |
| x4 | 0 | 1 | 1 | 1 | x4 | 0 | 0 | 1 | 1 |
1.
а) А = SÈT = {b, c, e, f, i};
А = SÇT = {c, e, i};
A = S\T = {b}; B = T\S = {f}:
A = SDT = {b, f}.
b) A = ùS = {a, d, f, g, h};
B = ùT = {a, b, d, g, h}.
c) SÄT = {{b, c}, {b, e}, {b, f}, {b, i}, {c, c}, {c, e}, {c, f}, {c, i}, {e, c}, {e, e}, {e, f}, {e, i}, {i, c}, {i, e}, {i, f}, {i, i}}.
2.
a) h3 =
| у | x1 | x2 | x3 |
| 2 | b | e | 6 |
| 3 | с | e | 5 |
| 5 | с | b | 2 |
| 4 | а | e | 5 |
| 3 | с | e | 6 |
| 4 | а | c | 5 |
|
| у | x1 | x2 | x3 |
| 3 | с | e | 5 |
| 4 | а | e | 5 |
|
3.
a)
| r3 | x1 | x2 | x3 | x4 |
| x1 | 1 | 1 | 0 | 1 |
| x2 | 1 | 1 | 0 | 1 |
| x3 | 1 | 1 | 1 | 0 |
| x4 | 0 | 1 | 1 | 1 |
| r4 | x1 | x2 | x3 | x4 |
| x1 | 1 | 1 | 0 | 1 |
| x2 | 0 | 1 | 0 | 0 |
| x3 | 0 | 0 | 0 | 0 |
| x4 | 0 | 0 | 1 | 1 |
| r3 | x1 | x2 | x3 | x4 |
| x1 | 0 | 0 | 0 | 0 |
| x2 | 0 | 0 | 0 | 1 |
| x3 | 1 | 0 | 1 | 0 |
| x4 | 0 | 1 | 0 | 0 |
| r3 | x1 | x2 | x3 | x4 |
| x1 | 0 | 0 | 0 | 0 |
| x2 | 1 | 0 | 0 | 1 |
| x3 | 1 | 1 | 1 | 0 |
| x4 | 0 | 1 | 0 | 0 |
У колоді 52 карти. У скількох випадках при виборі з колоди 10 карт серед них виявляться: а) рівно один туз; б) хоча б один туз; в) не менше двох тузів; г) рівно два тузи?
Відповідь:
а) Всього у колоді 4 тузи. Отже за правилом добутку перемножимо ймовірність вибору з чотирьох тузів одного туза та ймовірність вибору інших карт, тобто 9 з 48:
б) Хоча б один туз – це означає може бути і 4, і 3, і 2, і 1. Отже для розв'язку необхідно від ймовірності вибору 10 карт з 52 відняти ймовірність вибору 10 карт з 48:
в) Не менше двох тузів – означає, що з 10 карт буде 4, 3 або 2 тузи. Рішенням буде попередня відповідь від якої відняти ймовірність вибору 1 туза (першої відповіді):
г) Аналогічно розв'язку першого завдання отримаєм:
3. Задача 3
Граф заданий матрицею вагів. Побудувати для нього остов мінімальної ваги використовуючи алгоритми Пріма та Краскала, за алгоритмом Флойда обчислити найкоротші шляхи графа.

Відповідь:
Будова графа:
SHAPE \* MERGEFORMAT
| х1 |
| х2 |
| х4 |
| х3 |
| х5 |

Побудова остову мінімальної ваги по алгоритму Краскала:
Встановлюємо частковий порядок по вазі ребер графа:
| L13 | L15 | L14 | L12 | L23 | L45 | L34 | L35 | L24 | L25 |
| 8 | 8 | 9 | 11 | 12 | 12 | 14 | 15 | 18 | 20 |
SHAPE \* MERGEFORMAT
| х1 |
| х2 |
| х4 |
| х3 |
| х5 |

| Крок | Ребра остову | Вершини остову | |||||||
| L13 | L15 | L14 | L12 | x1 | x2 | x3 | x4 | x5 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 3 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Lij | 8 | 8 | 9 | 11 | L=8+8+9+11=36 | ||||
Будуємо матрицю вагів та матрицю переходів:
А0 =


Елементи матриці вагів будемо знаходити за формулою:
Ak [i; j] = min (Ak-1 [i; j], Ak-1 [i; k] + Ak-1 [k; j])
Перша ітерація: k=1
А1 =


Друга ітерація: k=2
А2 =


Третя ітерація: k=3
А3 =


Четверта ітерація: k=4
А4 =


П’ята ітерація: k=5
А5 =


4. Задача 4
Знайти мінімальну ДНФ логічної функції F = F (хг, х2, х3, х4), яка дорівнює одиниці на наборах 2, 3, 4, 11, 14, 15 і нулю на решті наборів.
Відповідь:
Спочатку необхідно подати функцію у ДДНФ.
ДДНФ =x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4
Виконуємо склеювання:
1-2 x1x2x3
1-4 x2x3x4
2-4 x2x3x4
4-6 x1x3x4
5-6 x1x2x3
ДДНФ = x1x2x3 Ú x2x3x4 Ú x2x3x4 Ú x1x3x4 Ú x1x2x3 Ú x1x2x3x4
1-2 x2x3
1-3 x2x3
2-3 x2x3
3-4 x3x4
4-5 x1x3
ДДНФ = x2x3 Ú x3x4 Ú x1x3 Ú x1x2x3x4
| ДДНФ | x1x2x3x4 | x1x2x3x4 | x1x2x3x4 | x1x2x3x4 | x1x2x3x4 | x1x2x3x4 |
| x2x3 | + | + | - | + | - | - |
| x3x4 | - | + | - | + | - | + |
| x1x3 | - | - | - | + | + | + |
| x1x2x3x4 | - | - | + | - | - | - |
min ДНФ = x1x3 Ú x2x3 Ú x1x2x3x4
Список використаної літератури
1. «Дискретна математика» С.Лук’яненко. К-2000
2. «Комбінаторика» Д.Сафонов. М-1992
3. «Комбінаторика для програмістів» В.Липський. М-1988
4. Конспект лекцій
5. Комп’ютерна мережа Інтернет