Министерство Образования, Молодежи и Спорта

Республики Молдова

Государственный университет Молдовы

Курсовая Работа

Тема:  Электрон в слое.

Работу выполнил студент 3-го курса: Радченко Андрей

Кишинёв 1997 г.
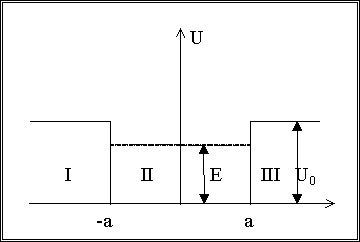
Микрочастица (электрон) в слое.

Собственно говоря, одномерная задача, которая сейчас будет рассмотрена, во многих учебных руководствах довольно подробно разобрана путём введения некоторых  упрощений.

Она состоит в следующем :

Микрочастица (электрон) движется вдоль оси x, и её движение полностью определяется следующим гамильтонианом :

 

ì -ћ2/(2m)׶2/¶x2 + U0  ,  x < -a

 Ù   ï

 H =        í -ћ2/(2m0)׶2/¶x2      ,  -a < x

ï

î -ћ2/(2m)׶2/¶x2 + U0  ,  x > a

Где  m   -   эффективная масса электрона в областях I , III ;

         m0 -   эффективная масса электрона в области II.

Запишем уравнение Шрёдингера для каждой области :

  ì ¶2YI/¶x2 + 2m/ћ2×(E - U0)YI = 0    ,  x £ -a

  ï

  í ¶2YII/¶x2 + 2m0/ћ2×E×YI = 0         ,  -a £ x £ a

ï

  î ¶2YIII/¶x2 + 2m/ћ2×(E - U0)×YI = 0         ,  x ³ a

Область I :   

Общий вид решения уравнения Шрёдингера для 1-ой области записывается сразу :

YI(x) = A×exp(n×x) + B×exp(-n×x).

Используя свойство ограниченности волновой функции, мы придём к тому что B = 0. Значит,

YI(x) = A×exp(n×x).

Волновая функция для второй области тоже элементарно определяется :

YII(x) = C×exp(i×k×x) + D×exp(-i×k×x).

Функция состояния для третьей области выглядит так :

YIII(x) = F×exp(-n×x).

Где

               k = (2m0×E/ћ2)1/2

               n = (2m×(U0-E)/ћ2)1/2.

Стратегия наших дальнейших действий будет состоять в следующем :

Напишем систему из  4  уравнений, удовлетворение которых эквивалентно удовлетворению функциями граничным условиям.

В этой системе из  4  уравнений будут фигурировать неизвестные коэффициенты  A,C,D и F. Мы составим линейную однородную систему относительно них.

Ясно, что существование нетривиальных решений допускается только в случае когда детерминант системы равен нулю. Как выяснится чуть позже, из этого весьма полезного факта мы извлечём уравнение, корнями которого будут возможные уровни энергии.

Приступим к осуществлению первого пункта, т.е. запишем условия сшивания волновых функций :

   YI(x=-a) = YII(x=-a)

YII(x=a) = YIII(x=a)

     YI¢(x=-a)/m = YII¢(x=-a)/m0

   YII¢(x=a)/m0 = YIII¢(x=a)/m

А в наших определениях этих функций это выглядит так :

A×exp(-n×a) = C×exp(-i×k×a) + D×exp(i×k×a)

m-1×A× n×exp(-n×a) = i×k×/m0×(C×exp(-i×k×a) - D×exp(i×k×a))

C×exp(i×k×a) + D×exp(-i×k×a) = F×exp(-n×a)

i×k×/m0×(C×exp(i×k×a) - D×exp(-i×k×a)) = - n/m×F×exp(-n×a).

Теперь составим определитель :

|exp(-n×a)      -exp(-i×k×a)                     -exp(i×k×a)                        0                         |

|m-1×n×exp(-n×a)                                     -1/m0×i×k×exp(-i×k×a)         1/m0×i×k×exp(i×k×a)     0            |

|0                  exp(i×k×a)                          exp(-i×k×a)                        -exp(-n×a)          |

|0                  1/m0×i×k×exp(i×k×a)              -1/m0×i×k×exp(-i×k×a)         1/m×n×exp(-n×a)|

Если теперь раскрыть этот определитель по обычным правилам и приравнять его к нулю, то мы получим следующее уравнение для уровней энергии:

((n/m)2 - (k/m0)2)×Sin(2×k×a) + 2×k×n/(m×m0)×Cos(2×k×a) = 0.

Это уравнение решается численным методом, а именно,  методом Ньютона.

Найдём неизвестные коэффициенты A, C, D, F для более полного описания волновой функции. Для этого воспользуемся некоторыми соотношениями, которые непосредственно вытекают из условий сшивания и условия нормировки.

C = F×exp(-n×a)×{exp(i×k×a) + exp(-3×i×k×a) ×( i×k/m0 - n/m)/(n/m + i×k/m0)}

D = C×exp(-2×i×k×a)×( i×k/m0 - n/m)/(n/m + i×k/m0)

A = exp(n×a)×(C×exp(-i×k×a) + D×exp(i×k×a)) .

Поскольку A, C и D линейно зависят от F, то целесообразно ввести обозначения :

A = RA×F

C = RC×F

D = RD×F.

RA, RC, RD - известные постоянные.

Таким образом, если мы каким-то образом узнаем константу F, то мы определим остальные константы A, C, D.  А сделаем мы это с помощью условия нормировки.

Действительно :

YI(x) = F×RA×exp(n×x)

YII(x) = F×( RC×exp(i×k×x) + RD×exp(-i×k×x)).

YIII(x) = F×exp(-n×x).

I1 + I2 + I3 = 1

Где

I1 = |F|2×|RA|2×òQexp(2×n×x)×dx = |F|2×|RA|2×(2×n)-1×exp(2×n×x) =

= |F|2×|RA|2×(2×n)-1×exp(-2×n×a)

I2 = |F|2×{ òL|RC|2×dx + òL|RD|2×dx + RC×RD*×òLexp(2×i×k×x)×dx +

+ RC*×RD×òLexp(-2×i×k×x)×dx } = |F|2×{ 2×a×(|RC|2 + |RD|2) +

((exp(2×i×k×a) - exp(-2×i×k×a))×RC×RD*/(2×i×k) +

+ i×((exp(-2×i×k×a) - exp(2×i×k×a))×RC*×RD/(2×k) }

I3 = |F|2×òWexp(-2×n×x)×dx = |F|2×(2×n)-1×exp(-2×n×a)

|F|2 = { |RA|2×(2×n)-1×exp(-2×n×a) + 2×a×(|RC|2 + |RD|2) +

((exp(2×i×k×a) - exp(-2×i×k×a))×RC×RD*/(2×i×k) +

+ i×((exp(-2×i×k×a) - exp(2×i×k×a))×RC*×RD/(2×k) + (2×n)-1×exp(-2×n×a) }-1.

Теперь, когда мы знаем  F, нетрудно определить коэффициенты A, C, D, а значит и волновую функцию, характеризующую состояние электрона.

  

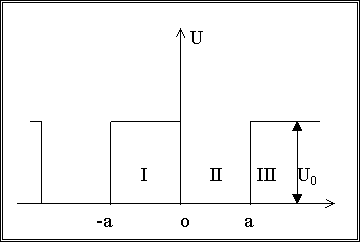
Электрон в слоях

Задача, которая сейчас будет описана, характеризуется тем, что потенциал обладает пространственной периодичностью. Схематически это изображается так.

То есть, это ни что иное как одномерное движение электрона в периодическом поле. Графически это можно изобразить серией потенциальных барьеров или, как говорят, серией потенциальных ступенек.

Аналитически условие периодичности потенциала записывается весьма просто:

U(x)=U(x+2a)    (1)

Соотношение (1) записано в предположении, что ширина каждой потенциальной ямы равна ширине всякого потенциального барьера.

Ясно, что волновые функции, соответствующие областям I, III, удовлетворяют одному и тому же уравнению Шредингера:

¶2Y/¶x2 + 2m/ћ2×(E - U0)Y = 0

следовательно эти функции отличаются только постоянным множителем, который называется фазовым множителем.

Этот фазовый множитель мы будем обозначать следующим образом:

r = exp(i 2ak)

Тогда Y(x+2ma) = Y(x)×rm ,     где  m=0, ±1, ±2,...                 (2)

Оказывается, что достаточным для определения дискретного энергетического спектра (рассматривается только случай когда E x > -a

его решение выглядит просто:

YI(x) = A×exp(n×x) + B×exp(-n×x).

Где n = (2m2 (U0-E) /ћ2)1/2

Рассмотрим область II:

Уравнение Шредингера для нее записывается в виде:

¶2YII/¶x2 + 2m1/ћ2×E YII = 0    ,  a ³ x ³ 0

его решение выглядит просто:

YII(x) = C×exp(i×p×x) + D×exp(-i×p×x).

Где  p = (2m1E/ћ2)1/2

Рассмотрим область III:

¶2YIII/¶x2 + 2m2/ћ2×(E - U0)YIII = 0    ,  2a > x > a

его решение выглядит просто:

YIII(x) = r (A×exp(n×x) + B×exp(-n×x)).

Запишем граничные условия:

YI(x=0) = YII(x=0)

YII(x=a) = YIII(x=a)

     YI¢(x=0)/m = YII¢(x=0)/m0

   YII¢(x=a)/m0 = YIII¢(x=a)/m

Подставляя волновые функции в эту систему уравнений, мы получим некоторые связи между коэффициентами A, B, C, D:

A+B=C+D

C exp(i p a)+D exp(-i p a) = exp(i 2 a k) (A exp(n a)+B exp(-n a))

(A-B) n/m2 = (C-D) i p / m1

(C exp(i p a)-D exp(-i p a)) i p / m1 = exp(i 2 a k) n/m2 (A exp(n a)-B exp(-n a))

Следуя приведённым выше соображениям, мы составим определитель :

|1                           1                                    -1                            -1                       |

|exp(i×k×2a+n×a)       exp(i×k×2a-n×a)               -exp(i×p×a)                -exp(-i×p×a)         |

|n/m2                       -n/m2                             -i×p/m1                     i×p/m1                         |

|n/m2exp(i×k×2a+n×a)                                      -n/m2×exp(i×k×2a-n×a)                           - i×p/m1×exp(i×p×a)                                        i×p/m1×exp(-i×p×a)            |

и приравняем его к нулю.

Результатом раскрытия определителя будет весьма громоздкое уравнение содержащее в качестве неизвестного энергию электрона.

Рассчитанные уровни энергии для различных эффективных масс приведены ниже.

a=10;      U=10;              m1=4;               m2=1

 

0.1135703312666857	0.6186359585387896	0.2019199605676639
0.3155348518478819	0.05047267055441365	1.263391478912778
0.4544326758658974	2.137353840637548	0.808172718170137
2.479933076698526	0.4544326758658974	6.168062551132728
5.611693924351967	1.820461802850339	1.529165865668653
1.023077302091622

                                                                                    

a=10       U=10               m1=2                m2=1

 

0.1032788024178655	0.2324238959628721	0.41331603936642
0.6460490460448886	0.930750939555283	1.26759057783714
1.656787195799296	2.098624192369327
2.593469359607937	3.141805331837109
3.744277072860902	5.887485640841992

a=10       U=10               m1=1                m2=1

0.05408120469105441	0.2163802958297131	0.4870681554965061
0.86644533469418	1.354969224117534	1.953300729714778
2.662383817919513	4.418966218448088	7.961581805911094

  

a=10       U=10               m1=0.5 m2=1

0.118992095909544	4.249561710930034	1.068004282376146
0.4754473139332004	5.78216724725356	2.955345679469631
1.895012565781256

a=10       U=10               m1=.25 m2=1

0.2898665804439349	4.30026851446248
2.479039415645616	1.132264393019809