| Курсовая работа Выполнил студент гр. 357-2 Карташов В. А. ТУСУР, Кафедра ТОЭ Томск 1999 Введение. 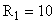 Ом Ом
 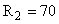 Ом Ом
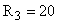 Ом Ом
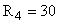 Ом Ом
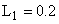 Гн Гн
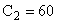 мкФ мкФ
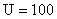 в в
 


1 Расчет переходного процесса в цепи при постоянном воздействии. Расчет граничных условий. А) 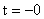 (ключ замкнут) (ключ замкнут) 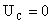 ; ; 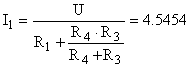 А А
Б) 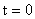 (ключ разомкнут) (ключ разомкнут) Независимые начальные условия: 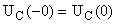 ; ; 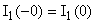 Согласно закону коммутации. Согласно закону коммутации.
В) 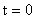 (ключ разомкнут) (ключ разомкнут)  
Зависимые начальные условия: 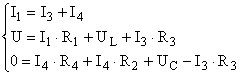 (1) (1)
В систему (1) подставляем 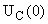 , , 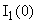 и находим и находим 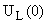 , , 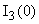 , , 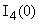 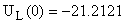 В В 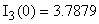 А А 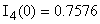 А А
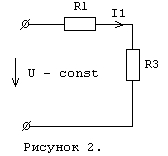 Г) Г) 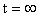 (ключ разомкнут) (ключ разомкнут)
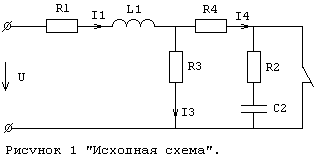
В послекоммутационном режиме схема изображена на рисунке 2. Находим токи 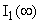 , , 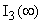 и и 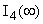 . . 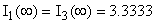 А А 
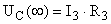 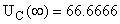 в в
Таблица 1. “Граничные условия” | | 
| 
| 
| 
| 
| |  | 4.5454 | 3.7879 | 0.7576 | 0 | -21.2121 | |  | 3.3333 | 3.3333 | 0 | 66.6666 | 0 | Расчёт  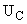 , ,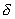 и и 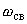 классическим методом. классическим методом. Составляем систему уравнений по законам Кирхкгоффа для схемы (Рис 1) в момент коммутации. 
Выразим 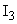 через через 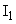 , , 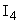 и воспользуемся формулами: и воспользуемся формулами: 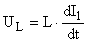 ; ; 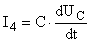 . . 
Из третьего уравнения выразим 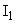 , найдём , найдём 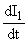 и подставим в второе. и подставим в второе. Для упрощения выражения подставим константы. 
Решая характеристическое уравнение  получаем корни 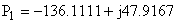  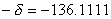  Общий вид 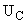 : : 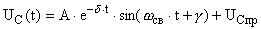 , в этом уравнении две неизвестных величины , в этом уравнении две неизвестных величины 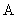 и и 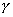 поэтому нужно ещё одно уравнение. Его можно найти если использовать соотношение поэтому нужно ещё одно уравнение. Его можно найти если использовать соотношение 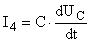 . . 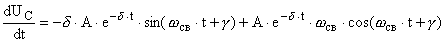 , получаем систему , получаем систему
уравнений: 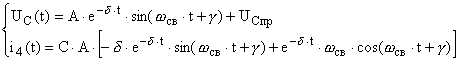 , , воспользуемся граничными условиями при t=0: 
подставив в систему известные константы выразим А из первого уравнения и подставив во второе найдем 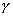 : : 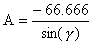 ; ; 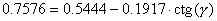 ; ;
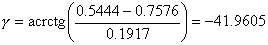 ; ; 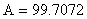 5; 5;

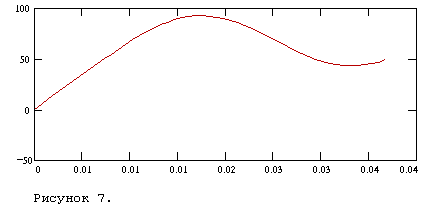
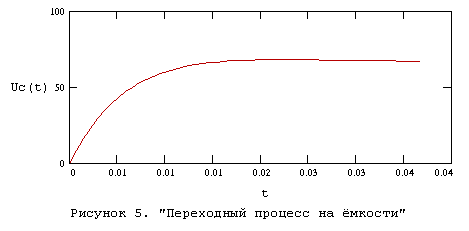
Переходный процесс на рисунке 5 изображен в период времени от 0 до 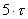 , где , где 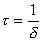 . . 1.3 Расчёт  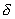 и и 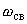 методом входного сопротивления. методом входного сопротивления.  
Внеся всё под общий знаменатель и приравняв числитель к нулю, получаем квадратное уравнение относительно P. 
Его решением являются корни  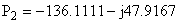 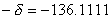  Рассчёт тока 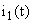 операторным методом. операторным методом. 
Схема преобразованая для рассчёта операторным методом изображена на рисунке 4. 
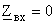 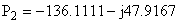 
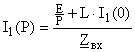 ; ; 
Выражение для тока имеет вид 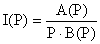 , оригинал будем искать в виде функции , оригинал будем искать в виде функции 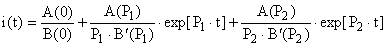 . . 
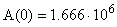 
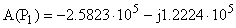 
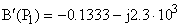 
Подставив все в выражение для тока получаем: 
Расчет переходного процесса в цепи при гармоническом воздействии. 2.1 Расчёт граничных условий. А) 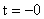 (ключ замкнут) (ключ замкнут) 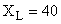 Ом; Ом; 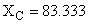 Ом Ом
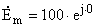 ; ; 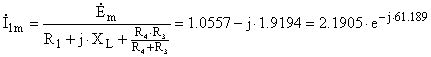 А А
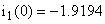 А; А; 
Б) 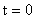 (ключ разомкнут) (ключ разомкнут) Независимые начальные условия: 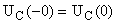 ; ; 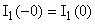 Согласно закону коммутации. Согласно закону коммутации.
В) 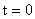 (ключ разомкнут) (ключ разомкнут)  
Зависимые начальные условия: 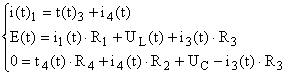 (1) (1)
В систему (1) подставляем 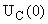 , , 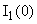 и находим и находим 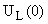 , , 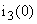 , , 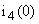 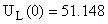 В В 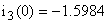 А А 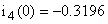 А А
Г) 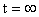 (ключ разомкнут) (ключ разомкнут) Находим токи 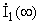 , , 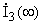 и и 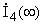 . . 



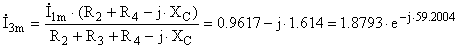 А А

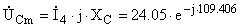 ; ; 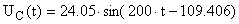 В В
Таблица 2. “Граничные условия” | | 
| 
| 
| 
| 
| |  | -1.9194 | -1.5984 | -0.3196 | 0 | 51.148 | | | | | | | | Нахождение 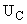 классическим методом. классическим методом. 
Воспользуемся граничными условиями. 


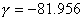 ; ; 

Переходный процесс на конденсаторе при гармоническом воздействии изображён на рисунке 6. 
Расчет переходного процесса в цепи при несинусоидальном воздействии. Так как схема является линейной, выполняется закон суперпозиции. Эту схему можно рассчитать методом наложения, т.е. для нахождения 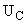 при несинусоидальном воздействии достаточно сложить ранее найденные при несинусоидальном воздействии достаточно сложить ранее найденные 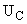 при постоянном воздействии и при постоянном воздействии и 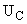 при синусоидальном воздействии. при синусоидальном воздействии.

Анализ зависимости типа переходного процесса в цепи от одного линейного параметра. Если в исходной схеме мы уменьшим ёмкость конденсатора в два раза то корни характеристического уравнения будут иными: 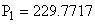 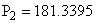 - действительными, разными. - действительными, разными.
Следовательно переходный процесс в этой цепи будет носить апериодический характер.
| 


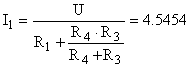 А
А 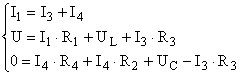 (1)
(1) Г)
Г) 

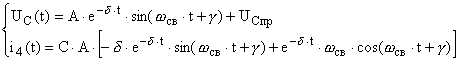 ,
, 




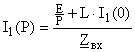 ;
; 
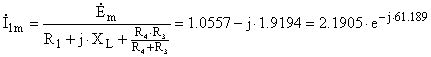 А
А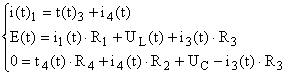 (1)
(1)