Курсовая на тему Исследование операций и Теория систем 3
Работа добавлена на сайт bukvasha.net: 2014-07-21Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Министерство образования и науки Российской Федерации
Южно-Уральский государственный университет
Кафедра Системы управления
Курсовая работа
по курсу
Исследование операций и Теория систем
Выполнил: Пушников А.А.
Группа: ПС-669
Проверила Плотникова Н.В.
Дата«____»____________2006г.
Челябинск
2006г
Содержание
Теория систем
Модели системы
Модель черного ящика
Модель состава
Модель структуры
Структурная схема
Динамическая модель
Классификация модели
Закономерности модели
Исследование операций
Задача 1
Задача 2
Задача 3
Задача 4

Рисунок 1. Рулевые органы ЛА
К выходам ЛА относятся данные, полученные с датчиков самолета. Непосредственно измеряется положение летательного аппарата в пространстве относительно нормальной системы координат, для этого используются датчики углового положения и система глобального позиционирования (GPS). Так же измеряются угловые скорости, угловые ускорения, линейные скорости и линейные ускорения (перегрузки).
· Аэродинамика летательного аппарата. Выражает воздушный поток вокруг самолета. Воздействие воздушного потока заключается в создании сил и моментов.
· Момент и сила тяги, вызываемые двигателем.
· Поступательное движение. Вычисляется скорость движения самолета в связной системе координат.
· Вращательное движение. Вычисляются угловые скорости самолета в связанной системе координат.
· Навигация. Вычисляет положение самолета в нормальной системе координат.
· Угловое положение. Через углы Эйлера или матрицу направляющих косинусов.
· Показания датчиков.
· Сигналы управляющих приводов. Положение ручка тяги, закрылок, элеронов, руля высоты и направления.
Таблица 1

Рисунок 2.Структурная схема.
– набор входных воздействий (входов) в системе – вектор управления (вход системы);
– набор выходных воздействий (выходов) в системе – набор данных получаемых с датчиков будет выходом системы;
– набор параметров, характеризующих свойства системы, постоянные во всё время рассмотрения, и влияющих на выходные воздействия системы, – конструктивные и неконструктивные параметры летательного аппарата;
– набор параметров, характеризующих свойства системы, изменяющиеся во время ее рассмотрения (параметры состояния) – линейные и угловые скорости, положение в пространстве и угловое положение, аэродинамические силы и моменты, силы и моменты в двигателе;
– параметр (или параметры) процесса в системе – t;
– правило  - нелинейная зависимость скоростей и положения в пространстве летательного аппарата от вектора управления;
- нелинейная зависимость скоростей и положения в пространстве летательного аппарата от вектора управления;
– правило  - нелинейная зависимость показаний датчиков от вектора управления, скоростей и положения в пространстве летательного аппарата;
- нелинейная зависимость показаний датчиков от вектора управления, скоростей и положения в пространстве летательного аппарата;
– правило  - нелинейная зависимость показаний датчиков от скоростей и положения в пространстве.
- нелинейная зависимость показаний датчиков от скоростей и положения в пространстве.
Тогда модель может быть записана так:


по их происхождению - искусственная система, машина;
по описанию входных и выходных процессов - c количественными переменными, непрерывная, детерминированная система;
по описанию оператора системы – параметризованная, разомкнутая, нелинейная;
по способам управления – система управляемая извне, с управлением типа регулирование;
2. Иерархичность. Совокупность управляющих элементов, датчиков, аэродинамической модели и модели двигателя дают летательному аппарату возможность управляемого движения в воздухе.
3. Коммуникативность. На полет летательного аппарата действуют температура окружающей среды, скорость и направление ветра, плотность воздуха и др.
4. Эквифинальность. Рано или поздно, самолет вынужден будет приземлится или разобьется. Т.о. скорости, ускорения, моменты и силы будут равны нулю.
Авиакомпания обслуживает два города. Первому городу требуется тоннаж в С1, а второму – в С2 т. Избыточный тоннаж не оплачивается. Каждый самолет в течение дня может выполнить только один рейс.
Расходы, связанные с перелетом самолетов по маршруту «центральный аэродром – пункт назначения», обозначены символом aij, где первый индекс соответствует номеру города, а второй – типу самолета.
А1=8, А2 = 15, А3 =12, В1 = 45, В2 = 7, В3 = 4, С1 = 20000, С2 = 30000, a11= 23,
a12 = 5, a13 = 1.4, a21 = 58, a22 = 10, a23 =3.8.
Решение
1. Составим математическую модель задачи. Возьмём в качестве целевой функции расходы на перелеты самолетов (соответственно, необходима минимизация целевой вункции), а в качестве переменных – число рейсов в день xij, где первый индекс соответствует номеру города, а второй – типу самолета.
Целевая функция:
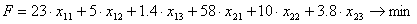
Ограничений задачи:
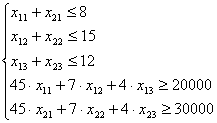
Основная задача линейного программирования:
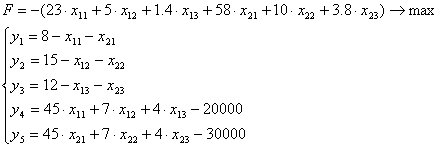
2. Правую часть уравнений (ограничения и целевую функцию) представляем в виде разности между свободным членом и суммой всех остальных:
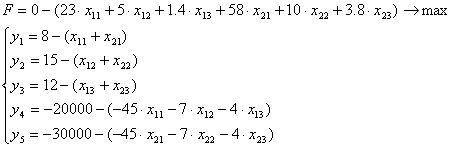
Составим симплекс – таблицу:
Южно-Уральский государственный университет
Кафедра Системы управления
Курсовая работа
по курсу
Исследование операций и Теория систем
Выполнил: Пушников А.А.
Группа: ПС-669
Проверила Плотникова Н.В.
Дата«____»____________2006г.
Челябинск
2006г
Содержание
Теория систем
Модели системы
Модель черного ящика
Модель состава
Модель структуры
Структурная схема
Динамическая модель
Классификация модели
Закономерности модели
Исследование операций
Задача 1
Задача 2
Задача 3
Задача 4
Теория систем
Модели системы
Рассматривается модель движения жесткого летательного аппарата самолетного типа. В качестве исследуемого аппарата взят некий гипотетический самолет современного типа.Модель черного ящика
К входам системы относятся управляющие органы летательного аппарата и возмущения окружающей среды. Рассматриваемый самолет обладает органом управления тягой двигателя и аэродинамическими рулями: элероны, закрылки, руль направления и высоты (рис. 1). Так же на самолет влияет скорость ветра, температура и плотность окружающего воздуха.
Рисунок 1. Рулевые органы ЛА
К выходам ЛА относятся данные, полученные с датчиков самолета. Непосредственно измеряется положение летательного аппарата в пространстве относительно нормальной системы координат, для этого используются датчики углового положения и система глобального позиционирования (GPS). Так же измеряются угловые скорости, угловые ускорения, линейные скорости и линейные ускорения (перегрузки).
Модель состава
Модель движения летательного аппарата можно разбить на следующие подсистемы и элементы:· Аэродинамика летательного аппарата. Выражает воздушный поток вокруг самолета. Воздействие воздушного потока заключается в создании сил и моментов.
· Момент и сила тяги, вызываемые двигателем.
· Поступательное движение. Вычисляется скорость движения самолета в связной системе координат.
· Вращательное движение. Вычисляются угловые скорости самолета в связанной системе координат.
· Навигация. Вычисляет положение самолета в нормальной системе координат.
· Угловое положение. Через углы Эйлера или матрицу направляющих косинусов.
· Показания датчиков.
· Сигналы управляющих приводов. Положение ручка тяги, закрылок, элеронов, руля высоты и направления.
Модель структуры
Структура движения летательного аппарата определяется отношениями между следующими парами элементов, указанны прямые отношения (табл. 1).Таблица 1
| Аэродинамические моменты | Угловые скорости |
| Аэродинамические силы | Угловые скорости |
| Аэродинамические силы | Аэродинамические моменты |
| Момент, вызываемый двигателем | Угловые скорости |
| Сила тяги | Скорость движения самолета |
| Сила тяги | Момент, вызываемый двигателем |
| Скорость движения самолета | Навигация |
| Навигация | Показания датчиков |
| Скорость движения самолета | Показания датчиков |
| Угловые скорости | Показания датчиков |
| Сигналы управляющих приводов | Аэродинамические моменты |
| Сигналы управляющих приводов | Аэродинамические силы |
| Сигналы управляющих приводов | Момент и сила тяги, вызываемые двигателем |
| Угловое положение | Угловые скорости |
Структурная схема
Так как в модели нас интересует функции каждого элемента системы, рассмотрим структурную схему в зависимости от сил и моментов, действующих на модель (рис. 2).| Fд |
| угловое положение |
| (x,y,z) |
| w |
| V |
| Mд |
| Ma |
| Fa |
| |
| Внешние воздействия |
| Навигация |
| Угловое положение |
| показания датчиков |
| Поступательное движение |
| Вращательное движение |
| Аэродинамика |
| Сила |
| Момент |
| Сила тяги |
| Момент двигателя |
| Сигналы приводов |

Рисунок 2.Структурная схема.
Динамическая модель
Обозначения:– набор входных воздействий (входов) в системе – вектор управления (вход системы);
– набор выходных воздействий (выходов) в системе – набор данных получаемых с датчиков будет выходом системы;
– набор параметров, характеризующих свойства системы, постоянные во всё время рассмотрения, и влияющих на выходные воздействия системы, – конструктивные и неконструктивные параметры летательного аппарата;
– набор параметров, характеризующих свойства системы, изменяющиеся во время ее рассмотрения (параметры состояния) – линейные и угловые скорости, положение в пространстве и угловое положение, аэродинамические силы и моменты, силы и моменты в двигателе;
– параметр (или параметры) процесса в системе – t;
– правило
– правило
– правило
Тогда модель может быть записана так:
Классификация модели
Классификация системы:по их происхождению - искусственная система, машина;
по описанию входных и выходных процессов - c количественными переменными, непрерывная, детерминированная система;
по описанию оператора системы – параметризованная, разомкнутая, нелинейная;
по способам управления – система управляемая извне, с управлением типа регулирование;
Закономерности модели
1. Целостность. Совокупность аэродинамической модели и модели двигателя дают летательному аппарату возможность движения в воздухе.2. Иерархичность. Совокупность управляющих элементов, датчиков, аэродинамической модели и модели двигателя дают летательному аппарату возможность управляемого движения в воздухе.
3. Коммуникативность. На полет летательного аппарата действуют температура окружающей среды, скорость и направление ветра, плотность воздуха и др.
4. Эквифинальность. Рано или поздно, самолет вынужден будет приземлится или разобьется. Т.о. скорости, ускорения, моменты и силы будут равны нулю.
Исследование операций
Задача 1
Авиакомпания «Небесный грузовик», обслуживающая периферийные районы страны, располагает А1 самолетами типа 1, А2 самолетами типа 2, А3 самолетами типа 3, которые она может использовать для выполнения рейсов в течение ближайших суток. Грузоподъемность (в тысячах тонн) известна: В1 для самолетов типа 1, В2 для самолетов типа 2, В3 для самолетов типа 3.Авиакомпания обслуживает два города. Первому городу требуется тоннаж в С1, а второму – в С2 т. Избыточный тоннаж не оплачивается. Каждый самолет в течение дня может выполнить только один рейс.
Расходы, связанные с перелетом самолетов по маршруту «центральный аэродром – пункт назначения», обозначены символом aij, где первый индекс соответствует номеру города, а второй – типу самолета.
А1=8, А2 = 15, А3 =12, В1 = 45, В2 = 7, В3 = 4, С1 = 20000, С2 = 30000, a11= 23,
a12 = 5, a13 = 1.4, a21 = 58, a22 = 10, a23 =3.8.
Решение
1. Составим математическую модель задачи. Возьмём в качестве целевой функции расходы на перелеты самолетов (соответственно, необходима минимизация целевой вункции), а в качестве переменных – число рейсов в день xij, где первый индекс соответствует номеру города, а второй – типу самолета.
Целевая функция:
Ограничений задачи:
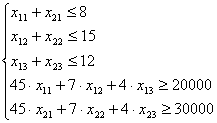
Основная задача линейного программирования:
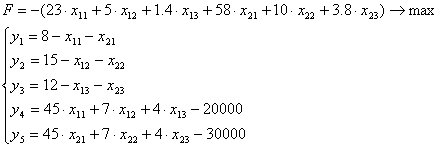
2. Правую часть уравнений (ограничения и целевую функцию) представляем в виде разности между свободным членом и суммой всех остальных:
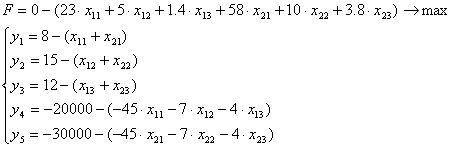
Составим симплекс – таблицу:
| bi | x11 | x12 | x13 | x21 | x22 | x23 | |||||||||||||
| 0 | 23 | 5 | 7/5 | 58 | 10 | 19/5 | |||||||||||||
| y1 | 8 | 1 | 0 | 0 | 1 | 0 | 0 | ||||||||||||
| y2 | 15 | 0 | 1 | 0 | 0 | 1 | 0 | ||||||||||||
| y3 | 12 | 0 | 0 | 1 | 0 | 0 | 1 | ||||||||||||
| y4 | -20000 | -45 | -7 | -4 | 0 | 0 | 0 | ||||||||||||
| y5 | -30000 | 0 | 0 | 0 | -45 | -7 | -4 | ||||||||||||
| bi | x11 | x12 | x13 | x21 | x22 | x23 | |||||||||||||
| 0 | 23 | 5 | 7/5 | 58 | 10 | 19/5 | |||||||||||||
| -150 | 0 | -10 | 0 | 0 | -10 | 0 | |||||||||||||
| y1 | 8 | 1 | 0 | 0 | 1 | 0 | 0 | ||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||||
| y2 | 15 | 0 | 1 | 0 | 0 | 1 | 0 | ||||||||||||
| 15 | 0 | 1 | 0 | 0 | 1 | 0 | |||||||||||||
| y3 | 12 | 0 | 0 | 1 | 0 | 0 | 1 | ||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||||
| y4 | -20000 | -45 | -7 | -4 | 0 | 0 | 0 | ||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||||
| y5 | -30000 | 0 | 0 | 0 | -45 | -7 | -4 | ||||||||||||
| 105 | 0 | 7 | 0 | 0 | 7 | 0 | |||||||||||||
| bi | x11 | x12 | x13 | x21 | y2 | x23 | ||||||||
| -150 | 23 | -5 | 7/5 | 58 | -10 | 19/5 | ||||||||
| -228/5 | 0 | 0 | -19/5 | 0 | 0 | -19/5 | ||||||||
| y1 | 8 | 1 | 0 | 0 | 1 | 0 | 0 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||
| x22 | 15 | 0 | 1 | 0 | 0 | 1 | 0 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||
| y3 | 12 | 0 | 0 | 1 | 0 | 0 | 1 | |||||||
| 12 | 0 | 0 | 1 | 0 | 0 | 1 | ||||||||
| y4 | -20000 | -45 | -7 | -4 | 0 | 0 | 0 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||
| y5 | -29895 | 0 | 7 | 0 | -45 | 7 | -4 | |||||||
| 48 | 0 | 0 | 4 | 0 | 0 | 4 | ||||||||
| bi | x11 | x12 | x13 | x21 | y2 | y3 | ||||||||
| -978/5 | 23 | -5 | -12/5 | 58 | -10 | -19/5 | ||||||||
| 464 | -58 | 0 | 0 | -58 | 0 | 0 | ||||||||
| y1 | 8 | 1 | 0 | 0 | 1 | 0 | 0 | |||||||
| 8 | 1 | 0 | 0 | 1 | 0 | 0 | ||||||||
| x22 | 15 | 0 | 1 | 0 | 0 | 1 | 0 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||
| x23 | 12 | 0 | 0 | 1 | 0 | 0 | 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||
| y4 | -20000 | -45 | -7 | -4 | 0 | 0 | 0 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||
| y5 | -29847 | 0 | 7 | 4 | -45 | 7 | 4 | |||||||
| 360 | 45 | 0 | 0 | 45 | 0 | 0 | ||||||||
| bi | x11 | x12 | x13 | y1 | y2 | y3 | ||||||||
| 1342/5 | -35 | -5 | -12/5 | -58 | -10 | -19/5 | ||||||||
| x21 | 8 | 1 | 0 | 0 | 1 | 0 | 0 | |||||||
| x22 | 15 | 0 | 1 | 0 | 0 | 1 | 0 | |||||||
| x23 | 12 | 0 | 0 | 1 | 0 | 0 | 1 | |||||||
| y4 | -20000 | -45 | -7 | -4 | 0 | 0 | 0 | |||||||
| y5 | -29487 | 45 | 7 | 4 | 45 | 7 | 4 | |||||||
Задача 2
| № вар | с1 | с2 | с3 | с4 | с5 | с6 | b1 | b2 | b3 | Знаки ограничений | a11 | a12 | a13 | a14 | ||||||||||||||||||
| 1 | 2 | 3 | ||||||||||||||||||||||||||||||
| 8 | 2 | 6 | 2 | –2 | 2 | 0 | 2 | 6 | 1 | = | = | = | –1 | 2 | 1 | 0 | ||||||||||||||||
| № вар. | a15 | a16 | a21 | a22 | a23 | a24 | a25 | a26 | a31 | a32 | a33 | a34 | a35 | a36 | Тип экстр. | |||||||||||||||||
| 8 | 0 | 0 | 2 | 1 | 1 | 1 | 2 | 0 | 1 | –1 | 0 | 0 | 1 | 0 | max | |||||||||||||||||


Правую часть уравнений (ограничения и целевую функцию) представляем в виде разности между свободным членом и суммой всех остальных:

2. Составим симплекс – таблицу:
| bi | x1 | x2 | ||||
| 2 | -4 | -6 | ||||
| x3 | 2 | -1 | 2 | |||
| x4 | 2 | 1 | 1 | |||
| x5 | 1 | 1 | -1 | |||
| bi | x1 | x2 | ||||
| 2 | -4 | -6 | ||||
| 6 | -3 | 3 | ||||
| x3 | 2 | -1 | 2 | |||
| 1 | -0.5 | 0.5 | ||||
| x4 | 2 | 1 | 1 | |||
| -1 | 0.5 | -0.5 | ||||
| x5 | 1 | 1 | -1 | |||
| 1 | -0.5 | 0.5 | ||||
| bi | x1 | x3 | ||||
| 8 | -7 | 3 | ||||
| 21/4 | 21/4 | -21/8 | ||||
| x2 | 1 | -0.5 | 0.5 | |||
| 3/8 | 3/8 | -3/16 | ||||
| x4 | 1 | 1.5 | -0.5 | |||
| 3/4 | 3/4 | -3/8 | ||||
| x5 | 2 | 0.5 | 0.5 | |||
| -3/8 | -3/8 | 3/16 | ||||
| bi | x4 | x3 | ||||
| 53/4 | 21/4 | 3/8 | ||||
| x2 | 11/8 | 3/8 | 5/16 | |||
| x1 | 3/4 | 3/4 | -3/8 | |||
| x5 | 13/8 | -3/8 | 11/16 | |||
Ответ: F=53/4, x1=3/4, x2=11/8, x3=0, x4=0, x5=13/8, x6=0.
Задача 3
| № вар. | а1 | а2 | а3 | b1 | b2 | b3 | b4 | b5 | с11 | с12 | с13 |
| 8 | 200 | 200 | 600 | 200 | 300 | 200 | 100 | 200 | 25 | 21 | 20 |
| № вар. | с14 | с15 | с21 | с22 | с23 | с24 | с25 | с31 | с32 | с33 | с34 | с35 |
| 8 | 50 | 18 | 15 | 30 | 32 | 25 | 40 | 23 | 40 | 10 | 12 | 21 |
| B1 | B2 | B3 | B4 | B5 | аi | |
| A1 | 25 | 21 | 20 | 50 | 18 | 200 |
| A2 | 15 | 30 | 32 | 25 | 40 | 200 |
| A3 | 23 | 40 | 10 | 12 | 21 | 600 |
| bi | 200 | 300 | 200 | 100 | 200 | 1000 |
| B1 | B2 | B3 | B4 | B5 | аi | |
| A1 | 25 | 21 | 20 | 50 | 18 | 200 |
| 200 | ||||||
| A2 | 15 | 30 | 32 | 25 | 40 | 600 |
| 300 | 200 | 100 | ||||
| A3 | 23 | 40 | 10 | 12 | 21 | 200 |
| 200 | ||||||
| bi | 200 | 300 | 200 | 100 | 200 | 600 |
r+m-1=7>5 это вырожденный случай.
Определение оптимального плана
1.
| B1 | B2 | B3 | B4 | B5 | аi | |
| A1 | 25 | 21 | 20 | 50 | 18 | 200+e1 |
| 200 | e1 | |||||
| A2 | 15 | 30 | 32 | 25 | 40 | 600 |
| 300 | 200 | 100 | ||||
| A3 | 23 | 40 | 10 | 12 | 21 | 200+e2 |
| e2 | 200 | |||||
| bi | 200 | 300+e1 | 200 | 100+e2 | 200 | 600+e1+e2 |
| B1 | B2 | B3 | B4 | B5 | аi | |
| A1 | 25 | 21 | 20 | 50 | 18 | 200+e1 |
| 0 | 200+e1 | |||||
| A2 | 15 | 30 | 32 | 25 | 40 | 600 |
| 200 | 100 | 200 | 100 | |||
| A3 | 23 | 40 | 10 | 12 | 21 | 200+e2 |
| e2 | 200 | |||||
| bi | 200 | 300+e1 | 200 | 100+e2 | 200 | 600+e1+e2 |
| B1 | B2 | B3 | B4 | B5 | аi | |
| A1 | 25 | 21 | 20 | 50 | 18 | 200+e1 |
| 0 | 200+e1 | |||||
| A2 | 15 | 30 | 32 | 25 | 40 | 600 |
| 200 | 100 | 200-e2 | 100+e2 | |||
| A3 | 23 | 40 | 10 | 12 | 21 | 200+e2 |
| e2 | 200 | |||||
| bi | 200 | 300+e1 | 200 | 100+e2 | 200 | 600+e1+e2 |
4.
| B1 | B2 | B3 | B4 | B5 | аi | |
| A1 | 25 | 21 | 20 | 50 | 18 | 200+e1 |
| 0 | e2+e1 | 200-e2 | ||||
| A2 | 15 | 30 | 32 | 25 | 40 | 600 |
| 200 | 300-e2 | 100+e2 | ||||
| A3 | 23 | 40 | 10 | 12 | 21 | 200+e2 |
| e2 | 200 | |||||
| bi | 200 | 300+e1 | 200 | 100+e2 | 200 | 600+e1+e2 |
5. Результат
6.
| B1 | B2 | B3 | B4 | B5 | аi | |
| A1 | 25 | 21 | 20 | 50 | 18 | 200+e1 |
| 0 | e2+e1 | 200-e2 | ||||
| A2 | 15 | 30 | 32 | 25 | 40 | 600 |
| 200 | 300-e2 | 100+e2 | ||||
| A3 | 23 | 40 | 10 | 12 | 21 | 200+e2 |
| 200 | e2 | |||||
| bi | 200 | 300+e1 | 200 | 100+e2 | 200 | 600+e1+e2 |
| B1 | B2 | B3 | B4 | B5 | аi | |
| A1 | 25 | 21 | 20 | 50 | 18 | 200 |
| 0 | 200 | |||||
| A2 | 15 | 30 | 32 | 25 | 40 | 600 |
| 200 | 300 | 100 | ||||
| A3 | 23 | 40 | 10 | 12 | 21 | 200 |
| 200 | ||||||
| bi | 200 | 300 | 200 | 100 | 200 | 600 |



Так в системе
Ответ: F=19100
Задача 4
| № | b1 | b2 | c11 | c12 | c22 | extr | a11 | a12 | a21 | a22 | p1 | p2 | Знаки огр. | |
| 1 | 2 | |||||||||||||
| 8 | 1 | 2 | –1 | 0 | –1 | max | 1 | 2 | 1 | 1 | 16 | 8 | £ | = |

Приведем систему к стандартному виду:

Определение стационарной точки:

Очевидно, что данные координаты не удовлетворяют условиям ограничений.
1. Проверка стационарной точки на относительный max или min:

Стационарная точка является точкой относительного максимума.
2. Составление функции Лагранжа:

3. Применим теорему Куна-Таккера:



Нахождение решения системы:
Перепишем эту систему, оставив все переменные в левой части:
Из уравнения 3 системы следует, что x1=8-x2:

Тогда:
Для обращения неравенств системы в равенства введём V1, V2, W и преобразуем систему:

Запишем условия дополняющей нежесткости:

4. Метод искусственных переменных:
Введем искусственные переменные

Далее решаем полученную задачу линейного программирования, для этого из 1 и 2 уравнений выражаем переменные
Составляем симплекс-таблицу:

| bi | x2 | u1 | u2 | V1 | V2 | |||||||
| -17M | -4M | -M | 0 | -M | M | |||||||
| M | M | 0.5M | -0.5M | 0 | -0.5M | |||||||
| z1 | 15 | 2 | -1 | 1 | 1 | 0 | ||||||
| 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | |||||||
| z2 | 2 | 2 | 2 | -1 | 0 | -1 | ||||||
| 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | |||||||
| W | 8 | -1 | 0 | 0 | 0 | 0 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | |||||||
| bi | x2 | z2 | u2 | V1 | V2 | |||||||
| -16M | -3M | 0.5M | -0.5M | -M | 0.5M | |||||||
| 3M | 3M | 1.5M | -1.5M | 0 | -1.5M | |||||||
| z1 | 16 | 3 | 0.5 | 0.5 | 1 | -0.5 | ||||||
| -3 | -3 | -1.5 | 1.5 | 0 | 1.5 | |||||||
| u1 | 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | ||||||
| 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | |||||||
| W | 8 | -1 | 0 | 0 | 0 | 0 | ||||||
| 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | |||||||
| bi | u1 | z2 | u2 | V1 | V2 | |||||||
| -13M | 3M | 2M | -2M | -M | -M | |||||||
| 13M | -3M | M | 2M | M | M | |||||||
| z1 | 13 | -3 | 1 | 2 | 1 | 1 | ||||||
| 13 | -3 | 1 | 2 | 1 | 1 | |||||||
| x2 | 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | |||||||
| W | 9 | 1 | 0.5 | -0.5 | 0 | -0.5 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | |||||||
| bi | u1 | z2 | u2 | z1 | V2 | |||||||
| 0 | 0 | 3M | 0 | M | 0 | |||||||
| V1 | 13 | -3 | 1 | 2 | 1 | 1 | ||||||
| x2 | 1 | 1 | 0.5 | -0.5 | 0 | -0.5 | ||||||
| W | 9 | 1 | 0.5 | -0.5 | 0 | -0.5 | ||||||
V1=13
x2=1
W=9
x1=8-x2=7

Ответ: x2=1, x1 =7,
Список используемой литературы
1. Волков И. К., Загоруйко Е. А. Исследование операций. – Москва: Издательство МГТУ имени Баумана Н. Э., 2000г. – 436с.2. Плотникова Н.В. «Исследование операций» Часть 1. Линейное программирование.
3. Плотникова Н.В. «Лекции по курсу теория систем»