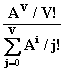| | | | | | | Курсовая работа Министерство науки и высшего образования Республики Казахстан Алматинский институт энергетики и связи Кафедра Автоматической электросвязи г. Алматы, 1999 г. Задание 1. Построить огибающую распределения вероятности занятия линии в пучке из V, на каждую из которых поступает интенсивность нагрузки а при условии, что: а) N >> V; б) N 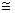 V; в) N, V V; в) N, V 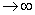 Для каждого используемого распределения рассчитать среднее число занятых линий и их дисперсию. Для расчета число линий в пучке определить из следующего выражения: V= 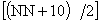 ; ; целая часть полученного числа, где NN – номер варианта. Средняя интенсивность нагрузки, поступающей на одну линию: а = 0,2+0,01 * NN Примечания: Для огибающей распределения привести таблицу в виде: В распределении Пуассона привести шесть – восемь составляющих, включая значение вероятности для i = 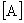 (целая часть А) (целая часть А) А = а * V Решение: Случайной называют такую величину, которая в результате эксперимента принимает какое то определенное значение, заранее не известное и зависящее от случайных причин, которые наперед предугадать невозможно. Различают дискретные и непрерывные случайные величины. Дискретная случайная величина определяется распределением вероятностей, непрерывная случайная величина – функцией распределения основными характеристиками случайной величины являются математическое ожидание и дисперсия. Определим исходные данные для расчета: V= a = 0.2 + 0.01 * 11 = 0.31 Эрл (средняя интенсивность нагрузки) А = а * V = 0,31 * 11 = 3,41 » 4 Эрл (нагрузка) а) Определим вероятности занятия линий в пучке из V = 11, при условии N >> V (N – число источников нагрузки). Для этого используем распределение Эрланга, представляющее собой усеченное распределение Пуассона, в котором взяты первые V+1 значения и пронумерованы так, чтобы сумма вероятностей была равна единице. Распределение Эрланга имеет вид: Pi(V) = 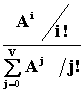 , , 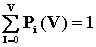 , , где Pi(V) – вероятность занятия любых i линий в пучке из V. Для определения составляющих распределения Эрланга можно применить следующее реккурентное соотношение: 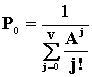
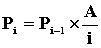
Математическое ожидание и дисперсия числа занятых линий соответственно равны: 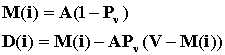
где Pv – вероятность занятости всех линий в пучке из V. Произведем расчет: Р0 = 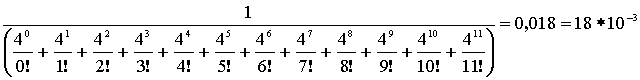 Р1 = Р0 * 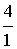 = 0,072 Р2 = Р1 * = 0,072 Р2 = Р1 * 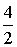 = 0,144 = 0,144 Р3 = Р2 *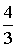 = 0,192 Р4 = Р3 * = 0,192 Р4 = Р3 *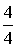 = 0,192 = 0,192 Р5= Р4 *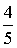 = 0,153 Р6 = Р5 * = 0,153 Р6 = Р5 *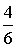 = 0,102 = 0,102 Р7 = Р6 *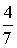 = 0,058 Р8 = Р7 * = 0,058 Р8 = Р7 *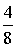 = 0,029 = 0,029 Р9 = Р8 *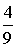 = 0,012 Р10 = Р9 * = 0,012 Р10 = Р9 * = 4,8 * 10-3 = 4,8 * 10-3 Р11 = Р10*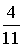 = 1,7 * 10-3 = 1,7 * 10-3 M( i ) = 4 * (1 - 1,7 * 10-3) = 3,99 D( i ) = 3,99 – 4 * 1,7 * 10-3 * (11 – 3,99) = 3,94 Данные результаты вычислений сведем в таблицу 1: Таблица 1 | P( i ) | 0,018 | 0,072 | 0,144 | 0,192 | 0,192 | 0,153 | 0,102 | 0,058 | 0,029 | 0,012 | 0,0048 | 0,0017 | | i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | б) Определим вероятность занятия линий в пучке из V=11, при условии N@V. Применим распределение Бернулли (биноминальное распределение), которое имеет вид: 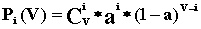
где: Pi(V) – вероятность занятия любых i линий в пучке из V; 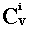 - число сочетаний из V по i (i = 0, V) - число сочетаний из V по i (i = 0, V)
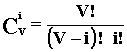 , ,
а – средняя интенсивность поступающей нагрузки на одну линию V-линейного пучка от N источников. Для вычисления вероятностей можно воспользоваться следующей рекурентной формулой: 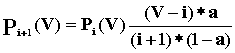
Математическое ожидание и дисперсия числа занятых линий соответственно равны: M( i ) = V*a; D( i ) = V * a * (1-a) Произведем расчет:  ; ; 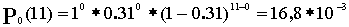
Р1 = 16,8*10-3*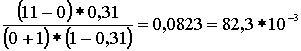 Р2 = 16,8*10-3* Р3 = 16,8*10-3*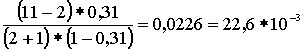 Р4 = 16,8*10-3*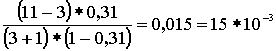 Р5 = 16,8*10-3*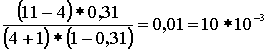 Р6 = 16,8*10-3*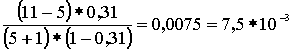 Р7 = 16,8*10-3* Р8 = 16,8*10-3*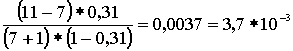 Р9 = 16,8*10-3* Р10 = 16,8*10-3*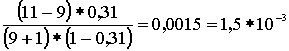 Р11 = 16,8*10-3*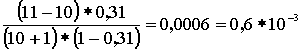 M( i ) = 11 * 0,31 = 3,41; D( i ) = 11 * 0,31 * (1 – 0,31) = 2,35 Результаты вычислений сведем в таблицу 2: Таблица 2 | P(i) *10-3 | 16,8 | 82,3 | 37,7 | 22,6 | 15 | 10 | 7,5 | 5,3 | 3,7 | 2,5 | 1,5 | 0,6 | | i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | в) Определим вероятность занятия линий в пучке из V=11 , при условии N,V®¥. Используем распределение Пуассона, как вероятность занятия i линий в бесконечном пучке линий за промежуток времени t:  , ,  , ,
где: l - параметр потока, выз/час lt – средняя интенсивность нагрузки поступающей на пучок линий (А=lt). Легко показать, что: 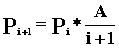 , , 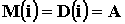
Произведем расчет: Р0 = 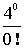 * е-4 = 0,018 Р1 = 0,018 * * е-4 = 0,018 Р1 = 0,018 * 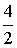 = 0,036 = 0,036 Р4 = 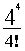 * 0,018 = 0,192 Р6 = 0,018 * * 0,018 = 0,192 Р6 = 0,018 *  = 0,102 = 0,102 Р8 = 0,018 * 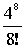 = 0,029 Р10 = 0,018 * = 0,029 Р10 = 0,018 * 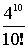 = 0,0052 = 0,0052 Р12 = 0,018 * 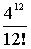 = 0,0006 = 0,0006 M( i ) = D( i ) = 4 Результаты вычислений сведем в таблицу 3: Таблица 3 | P( i ) | 0.018 | 0.036 | 0.192 | 0.102 | 0.029 | 0.0052 | 0.0006 | | i | 0 | 1 | 4 | 6 | 8 | 10 | 12 | По данным таблиц 1, 2, 3 построим графики огибающей вероятности для трех случаев: а) N>>V, б) N@V, в) N, V ® ¥ ; рис. 1. Задание 2. На коммутационную систему поступает простейший поток вызовов с интенсивностью А. Рассчитать вероятность поступления не менее к вызовов за промежуток времени [ 0, t*]: Рк(t*), где t* = 0,5; 1,0; 1,5; 2,0 Построить функцию распределения промежутков времени между двумя последовательными моментами поступления вызовов: F(t*), t* = 0; 0,1; 0,2; … Рассчитать вероятность поступления не менее к вызовов за интервал времени [ 0, t*]: Pi³k(t*), где t* = 1 Примечание: 1. Для расчета значений A и V взять из задания 1. 2.Число вызовов к определить из выражения: к = [V/2] - целая часть числа. Для построения графика взять не менее пяти значений F(t*). Результаты привести в виде таблицы: Расчет Pi³k(t*) провести не менее чем для восьми членов суммы. Решение: Потоком вызовов называют последовательность однородных событий, поступающих через случайные интервалы времени. Поток вызовов может быть задан тремя эквивалентными способами: Вероятностью поступления к вызовов за интервал времени [0,t). Функцией распределения промежутков времени между двумя последовательными моментами поступления вызовов. Вероятность поступления не менее к вызовов за интервал времени [0,t). Свойства потоков: станционарность, ординарность и полное или частичное отсутствие последействия. Потоки классифицируются с точки зрения наличия или отсутствия этих свойств. Основными характеристиками потоков вызовов являются: интенсивность m и параметр l. Простейшим потоком называется ординарный стационарный поток без последействия. Рассчитаем вероятность поступления не менее к вызовов за интервал времени [0,t). 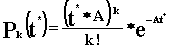 , ,
где: к = 0, 1, …; t* = t /`t ; где `t – средняя длительность обслуживания вызова. Определим данные для расчетов: К = 11/2 = 6; А = 4; V = 11; Производим расчеты для t* = 0,5 с. 
P2(0,5) = 0,13 P3(0,5) = 0,18 P4(0,5) = 0,09 P5(0,5) = 0,03 P6(0,5) = 0,012 Производим расчеты для t* = 1,0 с. 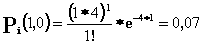
P2(1) = 0,14 P3(1) = 0,19 P4(1) = 0,19 P5(1) = 0,15 P6(1) = 0,1 Производим расчеты для t* = 1,5 с. 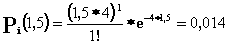
P2(1,5) = 0,044 P3(1,5) = 0,089 P4(1,5) = 0,13 P5(1,5) = 0,16 P6(1,5) = 0,16 Производим расчеты для t* = 2 с. 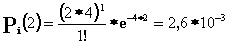
P2(2) = 0,01 P3(2) = 0,028 P4(2) = 0,057 P5(2) = 0,91 P6(2) = 0,122 Рассчитаем функцию распределения промежутков времени между двумя последовательными моментами поступления вызовов: 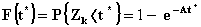
где Zk – промежуток времени между ( к-1 )-м и к-м вызовами. F(0) = 1 – e-4*0 = 0 F(0,1) = 1 – e-4*0,1 = 0,32 F(0,2) = 1 – e-4*0,2 = 0,55 F(0,3) = 0,69 F(0,4) = 0,79 F(0,5) = 0,86 F(0,6) = 0,9 F(0,7) = 0,93 Результаты вычислений занесем в таблицу 4: Таблица 4 | F( t* ) | 0 | 0,32 | 0,55 | 0,69 | 0,79 | 0,86 | 0,9 | 0,93 | | t* | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | Рассчитаем вероятность поступления не менее к вызовов за промежуток времени [0, t*): 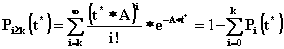 , при t*=1. , при t*=1.
 P6³6(1) = 1 – 0,84 = 0,16 P10³6(1) = 1 – 0,005 = 0,995 P6³6(1) = 1 – 0,84 = 0,16 P10³6(1) = 1 – 0,005 = 0,995
P7³6(1) = 1 – 0,05 = 0,95 P11³6(1) = 1 – 0,001 = 0,999 P8³6(1) = 1 – 0,02 = 0,98 P12³6(1) = 1 – 0,0006 = 0,9994 P9³6(1) = 1 – 0,013 = 0,987 P13³6(1) = 1 – 0,0001 = 0,9999 Интенсивность простейшего потока вызовов m численно равна параметру l, а при t = `t =1: m = l = А = 4. Задание 3. Рассчитать интенсивность поступающей нагрузки на входы I ГИ для АТСКУ – А вх. I ГИ. Рассчитать средние интенсивности удельных абонентских нагрузок для абонентских лини народно-хозяйственного и квартирного секторов : АНХ и АКВ , а так же среднюю удельную интенсивность нагрузки на абонентскую линию АТС - АИСХ . Пересчитать интенсивность нагрузки на выход ступени I ГИ. Исходные данные, таблица 5: Таблица 5 | Емкость N | NНХ | Nкв | СНХ | ТНХ | СКВ | ТКВ | NI ГИ | | 9000 | 5000 | 4000 | 3,8 | 100 | 1,5 | 130 | 1000 | Решение: 1. Основными параметрами интенсивности нагрузки являются: Ni – число источников нагрузки i-й категории. Ci – среднее число вызовов, поступающих от одного источника i-й категории в ЧНН (час наибольшей нагрузки). ti – средняя длительность одного занятия для вызова от источника i-й категории. Различают следующие категории источников нагрузки: абонентские линии народнохозяйственного сектора (НХ), абонентские линии квартирного сектора индивидуального пользования (кв.и.), абонентские линии квартирного сектора коллективного сектора (кв.к.), таксофоны (т). Для расчета используем две категории: абонентские линии народнохозяйственного сектора (НХ) и абонентские линии квартирного сектора (кв). Интенсивность поступающей нагрузки: 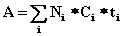 , ,
Средняя длительность одного занятия зависит от типа системы коммутации и определяется выражением: 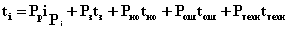
где: Рр – доля вызовов из общего числа, для которых соединения закончились разговором; Рз – доля вызовов из общего числа, для которых соединения не закончились разговором из-за занятости линии вызываемого абонента; Рно – то же из за неответа вызываемого абонента; Рош – то же из-за ошибок в наборе номера; Ртехн - то же из-за технических неисправностей в узлах коммутации (при расчетах Ртехн = 0); tрi , tз , tно , tош , tтехн – средние длительности занятий соответствующие этим случаям. Их можно определить из следующих выражений: tPi = ty+ tпв+ Ti+ t0 tз = ty+ tсз+ t0 tно = ty+ tпвн+ t0 tош = 18 с. где: tу – средняя длительность установления соединения; tпв и tпвн средняя длительность слушания сигнала «КПВ» (tпв=7 с. в случае разговора между абонентами; tпвн=30 с. в случае неответа вызываемого абонента); Ti – продолжительность разговора для вызова i-й категории; tо – продолжительность отбоя; tсз – продолжительность слушания сигнала “Занято” tу = 0,5* tМАВИ + tМРИ + tМРИ + tСО + n * tН + tIГИ + tМIГИ + tМСD + tМСD где tj – время ожидания обслуживания маркером j-й ступени; tj = 0,1 с. tМАВИ – время установления соединения маркером АВ на ступени АИ при исходящей связи; tМАВИ = 0,3 с. tМРИ - время установления соединения маркером ступени РИ; tМРИ = 0,2 с. tМIГИ - время установления соединения маркером ступени IГИ; tМIГИ = 0,65 с. tМСD - время установления соединения маркером CD; tМСD = 1 С. tСО – средняя длительность слушания сигнала «Ответ станции»; tСО = 3 с. tН – средняя длительность набора одного знака номера; tН = 1,5 с. n – значность номера. Значения tо и tсз для АТСКУ следующие: tсз = 0,6 с., tо = 0. РР = 0,6; Рз = 0,2; Рно = 0,15; Рош = 0,05; tу = 0,5 * 0,3 + 0,1 + 0,2 + 3 + 5 * 1,5 + 0,1 + 0,65 + 0,1 + 1 = 12,8 с. tрнх = 12.8 + 7 + 100 + 0.6 = 120,4 с. tркв = 12,8 + 7 + 130 + 0,6 = 150,4 с. РР* tрнх = 0,6 * 120,4 = 72,24 РР* tркв = 0,6 * 150,4 = 90,24 tз = tу+ tсз+ tо = 12,8+0+0,6 = 13,4 с. Рз* tз = 0,2*13,4 = 2,68 tно = tу+ tпвн+ tо = 12,8+30+0,6 = 43,4 с. Рно* tно =0,15*43,4 = 6,51 Рош* tош = 0,05*18 = 0,9 tнх = 72,24+2,68+6,51+0,9+0 = 82,33 с. tкв = 90,24+2,68+6,51+0,9+0 = 100,33 с. АВХIГИНХ = 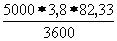 = 434,5 Эрл = 434,5 Эрл АВХIГИКВ = 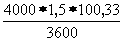 = 167,2 Эрл = 167,2 Эрл АВХIГИ = 434,5 + 167,2 = 601,7 Эрл 2. Рассчитаем средние интенсивности удельных абонентских нагрузок для абонентских линий народнохозяйственного и квартирного секторов: 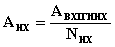 , Эрл , Эрл
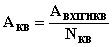 , Эрл , Эрл
Средняя удельная интенсивность нагрузки на абонентскую линию АТС: 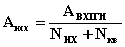 , Эрл , Эрл
АНХ = 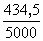 = 0,087 Эрл АКВ = = 0,087 Эрл АКВ = 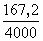 = 0,042 Эрл = 0,042 Эрл АИСХ = 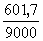 = 0,07 Эрл = 0,07 Эрл 3. Пересчитаем нагрузку со входа ступени I ГИ на ее выход: 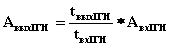 , ,
где tвхIГИ и tвыхIГИ – соответственно среднее время занятия входа ступени I ГИ и среднее время занятия выхода ступени I ГИ: tвыхIГИ = tвхIГИ - Dt, где Dt – разница между временами занятия на входе и выходе ступени I ГИ. Для АТСКУ: Dt = 0,5* tМАВИ + tМРИ + tМРИ + tСО + n * tН + tМIГИ + tМIГИ tВХIГИ = АВХIГИ / Nнх * Снх + Nкв * Скв Dt = 0,5 * 0,3 + 0,1 + 0,2 + 3 + 5 * 1,5 + 0,1 + 0,65 = 11,7 с. tВХIГИ = 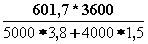 = 86,6 с. = 86,6 с. tВЫХIГИ = tВХIГИ - Dt = 86,6 – 11,7 = 74,9 с. АВЫХIГИ = 74,9/86,6 * 601,7 = 520,4 Эрл Задание 4. Рассчитать и построить зависимость числа линий V и коэффициента использования h (пропускная способность) от величины интенсивности нагрузки при величине потерь Р = 0,0NВ, где NВ – номер варианта. Результаты расчета представить в виде таблицы при Р = const (постоянная). | N | А, Эрл | V | Р (табл) | Y | h | | 1 2 3 4 . . . 10 | 1 3 5 10 . . . 50 | | | | | Решение: Вероятность занятия любых i линий в полнодоступном пучке из V при обслуживании простейшего потока вызовов определяется распределением Эрланга: 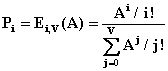
Различают следующие виды потерь: потери от времени Pt , потери по вызовам Pв , потери по нагрузке Pн . Потери по времени Pt - доля времени, в течение которого заняты все V линии пучка. Потери по вызовам определяются отношением числа потерянных вызовов Спот к числу поступивших Спост: Pв = Спот / Спост Потери по нагпрузке определяются отношением интенсивности потерянной нагрузки Yпот к интенсивности поступившей А : Pн = Yпот / А При обслуживании простейшего потока вызовов перечисленные выше три вида потерь совпадают Pt = Pв = Pн и равны вероятности занятия V линий в пучке: РV = Pt = Pв = Pн = EV,V(A) = 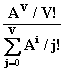 Обслуженной нагрузкой называют нагрузку на выходе коммутационной схемы, ее интенсивность определяют из выражения: Y = F - YПОТ = A * (1 - EV(A)) Среднее использование одной линии в пучке равно: h = Y / V При Р = 0,011 (11 вариант), по известным А, используя таблицы вероятности потерь определим соответствующие V и рассчитаем для каждого значения А интенсивность Y и среднее использование h. А = 1, Эрл V1=5 Y1=1(1-0,011) = 0,989 h = 0,197 А = 3, Эрл V3=8 Y3=3(1-0,011) = 2,96 h = 0,986 А = 5, Эрл V5=11 Y5=5(1-0,011) = 4,94 h = 0,449 А = 10, Эрл V10=18 Y10=10(1-0,011) = 9,89 h = 0,549 А = 15, Эрл V15=24 Y15=15(1-0,011) = 14,83 h = 0,617 А = 20, Эрл V20=30 Y20=20(1-0,011) = 19,78 h = 0,659 А = 25, Эрл V25=36 Y25=25(1-0,011) = 24,73 h = 0,686 А = 30, Эрл V30=42 Y30=30(1-0,011) = 29,67 h = 0,706 А = 40, Эрл V40=53 Y40=40(1-0,011) = 39,56 h = 0,746 А = 50, Эрл V50=64 Y50=50(1-0,011) = 49,45 h = 0,772 Результаты расчетов занесем в таблицу 6: Таблица 6 | N | А, Эрл | V | Р (табл) | Y | h | | 1 2 3 4 5 6 7 8 9 10 | 1 3 5 10 15 20 25 30 40 50 | 5 8 11 18 24 30 36 42 53 64 | 0,011 0,011 0,011 0,011 0,011 0,011 0,011 0,011 0,011 0,011 | 0,989 2,96 4,94 9,89 14,83 19,78 24,73 29,67 39,56 49,45 | 0,197 0,986 0,449 0,549 0,617 0,659 0,686 0,706 0,746 0,772 | Построим график зависимости числа линий V и коэффициента использования h от величины интенсивности нагрузки Y при величине Р=0,011. Задание 5. 1. Построить оптимальную равномерную неполнодоступную (НПД) схему, имеющую следующие параметры: V – емкость пучка, g – число нагрузочных групп, d – доступность. Привести матрицу связности. Исходные данные: V = 25*Nгр + NВ D = 10*Nгр где Nгр – номер группы , NВ – номер варианта. 8, если N8=1-10; g = 10, если N8=11-21 12, если N8=21-… 2. Рассчитать и построить зависимость числа линий V от величины потерь Р неполнодоступного пучка при значении A и D=10 по формуле Эрланга, О Делла, Пальма-Якобеуса. Результаты привести в виде таблицы и графика: | | Р | | V | | | | | | Формула Эрланга | О Делла | Пальма-Якобеуса | МПЯ* | | 1 2 3 | | | | | | *- Модифицированная формула Пальма-Якобеуса. Исходные данные: А – поступающая нагрузка взять в задании 1. Решение: Неполнодоступное включение это когда входу доступны не все, а часть выходов (d-определяет количеств |


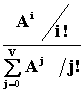 ,
, 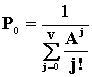
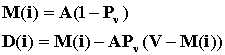
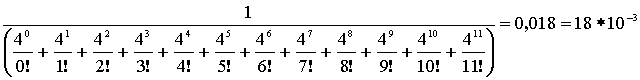
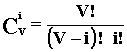 ,
,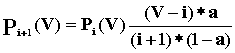
 ;
; 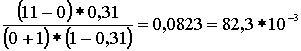

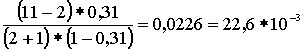
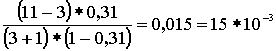
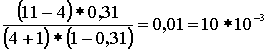
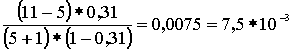

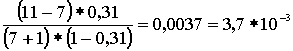

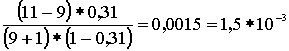
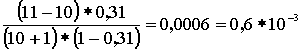
 ,
, 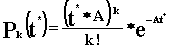 ,
,