Курсовая на тему Основы программирования в среде Qbasic
Работа добавлена на сайт bukvasha.net: 2014-12-09Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Федеральное агентство по образованию
Пермский государственный технический университет
по информатике
Преподаватель
Пермь 2008
Содержание
Введение
Исходные данные для разработки темы
Основная часть
1. Выполнение арифметических операций
2. Решение задач
2.1 Матрицы и определители
2.2 Решение систем линейных уравнений по формулам Крамера
2.3 Основы векторного исчисления
3. Графический режим Qbasic
3.1 Построение проекций
3.2 Построение графиков функций
3.3 Геометрические преобразования
Выводы и заключение
Список литературы
Введение
Бейсик (BASIC) – это сокращение английских слов Beginners All-purpouse Symbolic Instraction Code, что в переводе означает “многоцелевой язык символических инструкций для начинающих”. Он был разработан профессорами Дартмутского колледжа (США) Т. Куртцем и Дж. Кемени в 1965 году для обучения студентов, незнакомых с вычислительной техникой. Этот язык, напоминающий Фортран, но более простой, быстро стал очень популярным. Особенно его популярность повысилась с появлением персональных компьютеров, где он стал одним из основных языков программирования. Существует множество версий языка Бейсик и все они имеют особенности. В каждой из них можно выделить общее подмножество, в котором отражены характерные (стандартные) грамматика, синтаксис и семантика языка. Наиболее популярной версией является Qbasic, благодаря удобному интерфейсу и представлению пользователю ряда сервисных возможностей, присущих современным системам программирования. Поэтому тексты представленных в работе программ отлажены именно в ней.
Исходные данные для разработки темы
Ниже представлены исходные данные для разработки темы по предложенным заданиям в среде программирования Qbasic: выполнение арифметических операций, решение задач из курса высшей математики, построение графиков функций, выполнение геометрических преобразований.
Задание 1. Найти значение выражения:
1.1 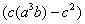
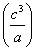
1.2 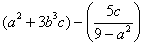
1.3 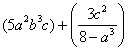
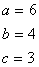
Задание 2. Найти сумму двух матриц
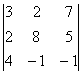
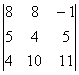
Задание 3. Найти произведение двух матриц
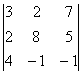

Задание 4. Вычислить определитель
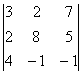
Задание 5. Решить систему уравнений по формулам Крамера
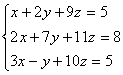
Задание 6. Даны векторы 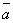
и 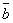
. Найти скалярное и векторное произведения векторов и угол между ними:
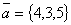
, 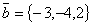
Задание 7. Найти объем пластины. Построить проекции, если
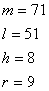
Задание 8. Построить графики функций
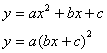
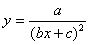
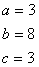
Задание 9. Выполнить последовательно геометрические преобразования:
- перенос;
- масштабирование;
- поворот относительно заданной точки.
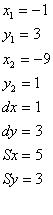
Точка поворота 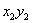
Угол поворота 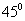
Основная часть
1. Выполнение арифметических операций
1.1 Найти значение выражения 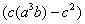
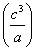
SHAPE \* MERGEFORMAT
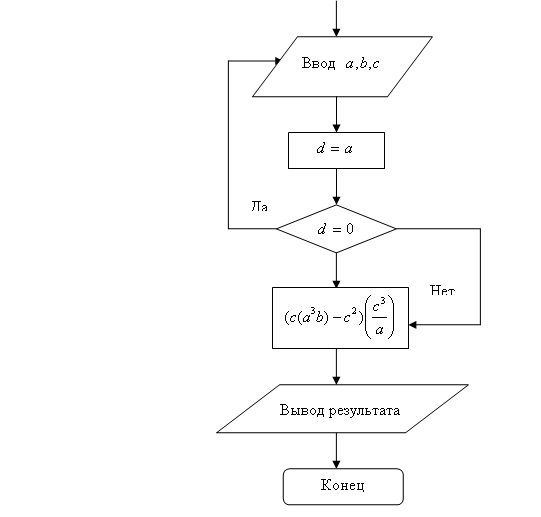
Рис. 1. Алгоритм вычисления
1.1.1 Программа, составленная с присвоением значений переменным
10 a = 6: b = 4: с = 3
20 d = a
30 IF d = 0 GOTO 60
40 END
50 PRINT (c * (a ^ 3 * b) - c ^ 2) * (c ^ 3 / a)
60 PRINT "а не должно быть 0"
70 GOTO 10
1.1.2 Программа, работающая в диалоговом режиме
10 INPUT "Введите a,b,c"; a, b, c
20 d = a
30 IF d = 0 GOTO 60
40 END
50 PRINT (c * (a ^ 3 * b) - c ^ 2) * (c ^ 3 / a)
60 PRINT "а не должно быть 0"
70 GOTO 10
Результат: 11623,5
1.2 Найти значение выражения 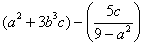
SHAPE \* MERGEFORMAT
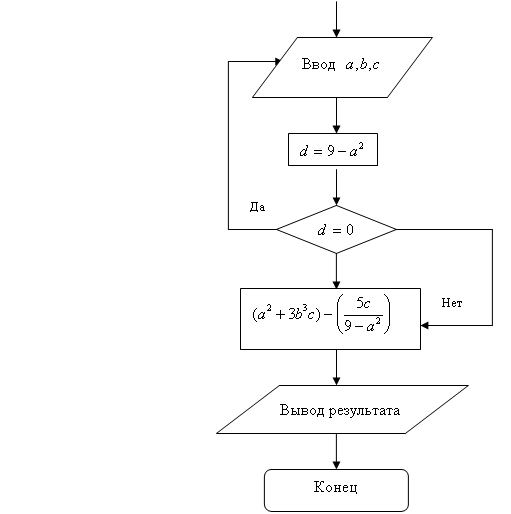
Рис.2. Алгоритм вычисления
1.2.1 Программа, составленная с присвоением значений переменным
10 a = 6: b = 4: с = 3
20 d = 9 – a^2
30 IF d = 0 GOTO 60
40 END
50 PRINT (a^2 + 3 * b ^ 3 * c) – (5 * c / (9 – a^2))
60 PRINT "а не должно быть 3 или -3"
70 GOTO 10
1.2.2 Программа, работающая в диалоговом режиме
10 INPUT "Введите a,b,c"; a, b, c
20 d = 9 – a^2
30 IF d = 0 GOTO 60
40 END
50 PRINT (a^2 + 3 * b ^ 3 * c) – (5 * c / (9 – a^2))
60 PRINT "а не должно быть 3 или -3"
70 GOTO 10
Результат: 612,5555
SHAPE \* MERGEFORMAT
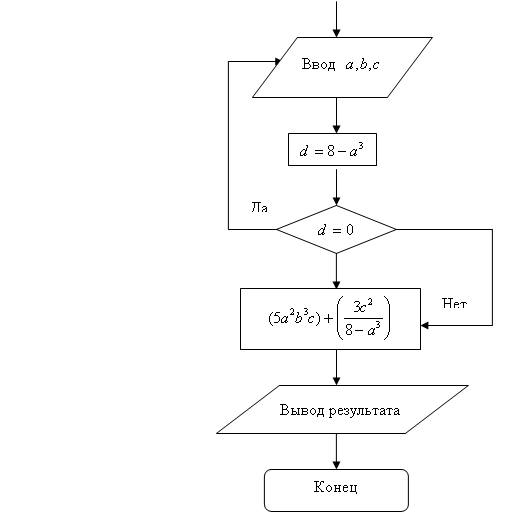
Рис.3. Алгоритм вычисления
1.3.1 Программа, составленная с присвоением значений переменным
10 a = 6: b = 4: с = 3
20 d = 8 – a^3
30 IF d = 0 GOTO 60
40 END
50 PRINT (5 * a^2 * b ^ 3 * c) + (3 * c^2 / (8 – a^3))
60 PRINT "а не должно быть 2 или -2"
70 GOTO 10
1.3.2. Программа, работающая в диалоговом режиме
10 INPUT "Введите a,b,c"; a, b, c
20 d = 8 – a^3
30 IF d = 0 GOTO 60
40 END
50 PRINT (5 * a^2 * b ^ 3 * c) + (3 * c^2 / (8 – a^3))
60 PRINT "а не должно быть 2 или -2"
70 GOTO 10
Результат: 34559,87
2. Решение задач
2.1 Матрицы и определители
2.1.1 Найти сумму двух матриц

Рис.4. Алгоритм вычисления
Программа нахождения суммы двух матриц
CLS
PRINT BBЕDИTЕ(A)
INPUT "BBЕDИTЕ a11,a12,a13"; a11, a12, a13
INPUT "BBЕDИTЕ a21,a22,a23"; a21, a22, a23
INPUT "BBЕDИTЕ a31,a32,a33"; a31, a32, a33
CLS
PRINT BBЕDИTЕ(B)
INPUT "BBЕDИTЕ b11,b12,b13"; b11, b12, b13
INPUT "BBЕDИTЕ b21,b22,b23"; b21, b22, b23
INPUT "BBЕDИTЕ b31,b32,b33"; b31, b32, b33
CLS
PRINT a11 + b11; a12 + b12; a13 + b13
PRINT a21 + b21; a22 + b22; a23 + b23
PRINT a31 + b31; a32 + b32; a33 + b33
END
Результат: 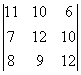
2.1.2 Найти произведение двух матриц


Рис.5. Алгоритм вычисления
Программа нахождения произведения двух матриц
CLS
PRINT BBЕDИTЕ(A)
INPUT "BBЕDИTЕ a11,a12,a13"; a11, a12, a13
INPUT "BBЕDИTЕ a21,a22,a23"; a21, a22, a23
INPUT "BBЕDИTЕ a31,a32,a33"; a31, a32, a33
CLS
PRINT BBЕDИTЕ(B)
INPUT "BBЕDИTЕ b11,b12,b13"; b11, b12, b13
INPUT "BBЕDИTЕ b21,b22,b23"; b21, b22, b23
INPUT "BBЕDИTЕ b31,b32,b33"; b31, b32, b33
CLS
PRINT a11 * b11 + a12 * b21 + a13 * b31; a11 * b12 + a12 * b22 + a13 * b32; a11 * b13 + a12 * b23 + a13 * b33 PRINT a21 * b11 + a22 * b21 + a23 * b31; a21 * b12 + a22 * b22 + a23 * b32; a21 * b13 + a22 * b23 + a23 * b33 PRINT a31 * b11 + a32 * b21 + a33 * b31; a31 * b12 + a32 * b22 + a33 * b32; a31 * b13 + a32 * b23 + a33 * b33 END
Результат: 
2.1.3 Вычислить определитель


Рис.6. Алгоритм вычисления
Программа вычисления определителя
PRINT BBЕDИTЕ(A)
INPUT "BBЕDИTЕ a1,b1,c1"; a1, b1, c1
INPUT "BBЕDИTЕ a2,b2,c2"; a2, b2, c2
INPUT "BBЕDИTЕ a3,b3,c3"; a3, b3, c3
PRINT a1 * b2 * c3 + b1 * c2 * a3 + a2 * b3 * c1 - a3 * b2 * c1 - b3 * c2 * a1 - a2 * b1 * c3
Результат: -163
2.1.4 Решить систему уравнений по формулам Крамера



Рис.7. Алгоритм вычисления
Программа решения системы уравнений по формулам Крамера
10 INPUT "BBЕDИTЕ KОЭФФИЦИЕHTЫ ПЕРВОГО УРАВНЕНИЯ"; a1, b1, c1, d1
20 INPUT "BBЕДИTЕ КОЭФФИЦИЕНТЫ ВТОРОГО УРАВНЕНИЯ"; a2, b2, c2, d2
30 INPUT "BBЕДИТЕ КОЭФФИЦИЕНТЫ ТРЕТЬЕГО УРАВНЕНИЯ"; a3, b3, c3, d3
40 d = a1 * b2 * c3 + b1 * c2 * a3 + a2 * b3 * c1 - a3 * b2 * c1 - b3 * c2 * a1 - a2 * b1 * c3
50 IF d = 0 GOTO 90
60 PRINT "x= "; (d1 * b2 * c3 + b1 * c2 * d3 + d2 * b3 * c1 - d3 * b2 * c1 - b3 * c2 * d1 - d2 * b1 * c3) / d
70 PRINT "y= "; (a1 * d2 * c3 + d1 * c2 * a3 + a2 * d3 * c1 - a3 * d2 * c1 - d3 * c2 * a1 - a2 * d1 * c3) / d
80 PRINT "z= "; (a1 * b2 * d3 + b1 * d2 * a3 + a2 * b3 * d1 - a3 * b2 * d1 - b3 * d2 * a1 - a2 * b1 * d3) / d
90 END
Результат: x=0,32; y=0,36; z=0,44
2.2 Основы векторного исчисления
Даны векторы 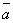
и 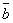
. Найти скалярное и векторное произведения векторов и угол между ними



Рис.8. Алгоритм вычисления
Программа нахождения скалярного и векторного произведения векторов, угла между ними
INPUT "BBЕДИТЕ КООРДИНАТЫ ПЕРВОГО ВЕКТОРА"; x1, y1, z1
INPUT "BBЕДИТЕ КООРДИНАТЫ ВТОРОГО ВЕКТОРА "; x2, y2, z2
ska = x1 * x2 + y1 * y2 + z1 * z2
PRINT "СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ = "; ska
x3 = y1 * z2 - z1 * y2
y3 = x1 * z2 - z1 * x2
z3 = x1 * y2 - y1 * x2
PRINT "BEKTOPHOE ПPOUЗBEДEHИE a*b= "; x3, y3, z3
a = (x1 ^ 2 + y1 ^ 2 + z1 ^ 2) ^ (1 / 2)
b = (x2 ^ 2 + y2 ^ 2 + z2 ^ 2) ^ (1 / 2)
ugl = ska / (a * b)
PRINT "КОСИНУС УГЛА МЕЖДУ ВЕКТОРАМИ РАВЕН"; ugl
Результат: -14; 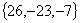
; -0,367658
3. Графический режим Qbasic
3.1 Построение проекции
Задание. Найти объем пластины и построить ее проекции.
Программа выполнения
m = 71
L = 51
H = 8
R = 9
SCREEN 12
WINDOW (0, 0)-(120, 90)
LINE (90, 90)-(90, 0)
LINE (0, 30)-(120, 30)
LINE (90 - 1.1 * m, 30 + .1 * m)-(90 - .1 * m, 30 + .1 * m + L), , B
LINE (90 - 1.1 * m, 30 - .1 * m - H)-(90 - .1 * m, 30 - .1 * m), , B
LINE (90 + .1 * m, 30 + .1 * m)-(90 + .1 * m + H, 30 + .1 * m + L), , B
CIRCLE (90 - 1.1 * m + .1 * m + R, 30 + L - R), R
CIRCLE (90 - .1 * m - .1 * m - R, 30 + .1 * m + .1 * m + R), R
CIRCLE (90 - .1 * m - .1 * m - R, 30 + .1 * m + L - .1 * m - R), R
CIRCLE (90 - 1.1 * m + .1 * m + R, 30 + .2 * m + R), R PRINT " ОБЪЕМ РАВЕН"; m * L * H
3.2 Построение графиков функций
3.2.1 Построить график функции 
Программа построения графика
SCREEN 12
WINDOW (-7, -6)-(7, 80)
X1 = -7: X2 = 4
H = (X2 - X1) / 100
Y1 = 3 * X1 ^ 2 + 8 * X1 + 3
PSET (X1, Y1)
FOR X = X1 TO X2 STEP H
Y = 3 * X ^ 2 + 8 * X + 3
LINE -(X, Y)
NEXT
3.2.2 Построить график функции 
Программа построения графика
SCREEN 12
WINDOW (-1, -6)-(1, 40)
X1 = -2: X1 = 2
H = (X2 - X1) / 100
Y1 = 192 * X1 ^ 2 + 144 * X1 + 27
PSET (X1, Y1)
FOR X = X1 TO X2 STEP H
Y = 192 * X ^ 2 + 144 * X + 27
NEXT
3.2.3 Построить график функции 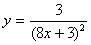
Программа построения графика
DEF FNA (X) = 3 / (8 * X + 3) ^ 2 SCREEN 12
WINDOW (-5, -5)-(5, 5)
X1 = -5: Y1 = FNA(X1)
X2 = -.4
X3 = -.3: Y3 = 27
X4 = 5
H = (X2 - X1) / 100
PSET (X1, Y1)
FOR X = X1 TO X2 STEP H
Y = FNA(X)
LINE -(X, Y)
NEXT
H = (X4 - X3) / 100
PSET (X3, Y3)
FOR X = X3 TO X4 STEP H
Y = FNA(X)
LINE -(X, Y)
NEXT
3.3 Геометрические преобразования
Выполнить последовательно геометрические преобразования:
- перенос;
- масштабирование;
- поворот относительно заданной точки.
Программа выполнения геометрических преобразований
SCREEN 12
WINDOW (-50, -10)-(20, 20)
X1 = -1
Y1 = 3
X2 = -9
Y2 = 1
DX = 1
DY = 3
SX = 5
SY = 3
LINE (X1, Y1)-(X2, Y2)'
LINE (X1 + DX, Y1 + DY)-(X2 + DX, Y2 + DY)'
LINE (X1 * SX, Y1 * SY)-(X2 * SX, Y2 * SY)'
LINE (8, 2)-(0, 0)
LINE ((X1 * COS(PI / 4) - Y1 * SIN(PI / 4)), (Y1 * SIN(PI / 4) + Y1 * COS(PI / 4)))-((0 * COS(PI / 4) - 0 * SIN(PI / 4)), (0 * SIN(PI / 4) + 0 * COS(PI / 4)))'
В работе представлены задания, направленные на овладение основами программирования в указанной среде: выполнение арифметических операций, решения задач из курса высшей математики, графические возможности.
В результате ее выполнения разработаны программы, охватывющие основные возможности версии, позволяющие выполнять все необходимые действия по составлению, отладке и выполнению программ.
В среде Qbasic существует несколько экранных режимов. Основной исходный экран представляет поле редактирования текста программы. Встроенный текстовый редактор выполняет две функции – редактирования текста и синхронной интерпретации строки. В этой связи строки в некоторых программах не нумеровались. Результаты работы программы, комментарии и сообщения интерпретатора представлялись в текстовом экране (по умолчанию режим SCREEN 0). При работе с графикой изображения строились в графическом экране, который имеет несколько режимов.
Особый интерес представляла система помощи help (подсказок), имеющая контекстную структуру с возможностью копирования примеров из текста подсказок, что позволило освоить работу с языком программирования Qbasic практически самостоятельно.
Таким образом, основная цель курсовой работы по овладению основами программирования в среде Qbasic выполнена.
Список литературы
1. Могилев А.В. Информатика. – М., 1999. – 816 с.
2. Сафронов И.К. Бейсик в задачах и примерах. –– СПб.: BHV, 2001. – 215 с.
3. Семашко Г.Л. Программирование для всех. – М.: Наука, 1986. – 325 с.
4. Ставнистый Н.Н. Qbasic в математике. Решение задач с помощью компьютера. Ч1. – М.: СОЛОН-Р, 2001. – 143 с.
5. Федоренко Ю. Алгоритмы и программы на QBASIC. - СПб.: Питер, 2002. – 287 с.
6. Хомоненко А.Д. Основы современных компьютерных технологий. – СПб.: КОРОНА принт, 1998. – 448 с.
7. Чернов Б.И. Программирование на алгоритмических языках Бейсик, Фортран, Паскаль. – М.: Просвещение, 1991. – 192 с.
Пермский государственный технический университет
Кафедра «Конструирование машин и сопротивление материалов»
КУРСОВАЯ РАБОТАпо информатике
Вариант 11
Выполнил
студент гр. ПО-03
ПроверилПреподаватель
Пермь 2008
Содержание
Введение
Исходные данные для разработки темы
Основная часть
1. Выполнение арифметических операций
2. Решение задач
2.1 Матрицы и определители
2.2 Решение систем линейных уравнений по формулам Крамера
2.3 Основы векторного исчисления
3. Графический режим Qbasic
3.1 Построение проекций
3.2 Построение графиков функций
3.3 Геометрические преобразования
Выводы и заключение
Список литературы
Введение
С развитием и совершенствованием ЭВМ тесно связано появление средств программирования. Для машин первого поколения они составлялись в машинных кодах. Это был трудоемкий процесс, поскольку программисту самому приходилось распределять память под программу, исходные данные и результаты. Разобраться в такой программе, модифицировать ее было практически невозможно. Еще в период перехода к машинам второго поколения (50-е годы) возникла необходимость в создании больших и сложных программ. Процесс их составления в машинных кодах резко снижал эффективность использования ЭВМ. Этот период характеризовался появлением первых алгоритмических языков программирования. Они отличались наглядной формой реализации алгоритма, использованием привычной математической символики, ограниченным набором ключевых слов. Основное их достоинство - универсальность.
Работа с программой, выполненной на алгоритмическом языке, очень упрощалась за счет относительной простоты написания, возможности модифицирования. Совершенствование вычислительной техники, а именно увеличение объема памяти и быстродействия машин, делало программирование на алгоритмических языках все более распространенным и перспективным. В настоящее время существует большое количество алгоритмических языков, которым присущи как общие, так и отличительные черты. Это Фортран, Бейсик, Паскаль и др. На их примере можно наглядно увидеть те характерные особенности, которые присущи программированию на алгоритмических языках вообще.Бейсик (BASIC) – это сокращение английских слов Beginners All-purpouse Symbolic Instraction Code, что в переводе означает “многоцелевой язык символических инструкций для начинающих”. Он был разработан профессорами Дартмутского колледжа (США) Т. Куртцем и Дж. Кемени в 1965 году для обучения студентов, незнакомых с вычислительной техникой. Этот язык, напоминающий Фортран, но более простой, быстро стал очень популярным. Особенно его популярность повысилась с появлением персональных компьютеров, где он стал одним из основных языков программирования. Существует множество версий языка Бейсик и все они имеют особенности. В каждой из них можно выделить общее подмножество, в котором отражены характерные (стандартные) грамматика, синтаксис и семантика языка. Наиболее популярной версией является Qbasic, благодаря удобному интерфейсу и представлению пользователю ряда сервисных возможностей, присущих современным системам программирования. Поэтому тексты представленных в работе программ отлажены именно в ней.
Исходные данные для разработки темы
Ниже представлены исходные данные для разработки темы по предложенным заданиям в среде программирования Qbasic: выполнение арифметических операций, решение задач из курса высшей математики, построение графиков функций, выполнение геометрических преобразований.
Задание 1. Найти значение выражения:
1.1
1.2
1.3
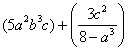
Задание 2. Найти сумму двух матриц
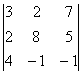

Задание 3. Найти произведение двух матриц
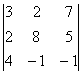

Задание 4. Вычислить определитель
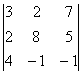
Задание 5. Решить систему уравнений по формулам Крамера
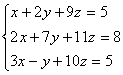
Задание 6. Даны векторы
Задание 7. Найти объем пластины. Построить проекции, если
Задание 8. Построить графики функций
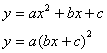
Задание 9. Выполнить последовательно геометрические преобразования:
- перенос;
- масштабирование;
- поворот относительно заданной точки.
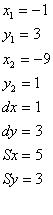
Точка поворота
Угол поворота
Основная часть
1. Выполнение арифметических операций
1.1 Найти значение выражения
| Начало |
SHAPE \* MERGEFORMAT
| |
| |
| |
| Вывод результата |
| Да |
| Нет |
| Ввод |
| Конец |

Рис. 1. Алгоритм вычисления
1.1.1 Программа, составленная с присвоением значений переменным
10 a = 6: b = 4: с = 3
20 d = a
30 IF d = 0 GOTO 60
40 END
50 PRINT (c * (a ^ 3 * b) - c ^ 2) * (c ^ 3 / a)
60 PRINT "а не должно быть 0"
70 GOTO 10
1.1.2 Программа, работающая в диалоговом режиме
10 INPUT "Введите a,b,c"; a, b, c
20 d = a
30 IF d = 0 GOTO 60
40 END
50 PRINT (c * (a ^ 3 * b) - c ^ 2) * (c ^ 3 / a)
60 PRINT "а не должно быть 0"
70 GOTO 10
Результат: 11623,5
1.2 Найти значение выражения
| Начало |
SHAPE \* MERGEFORMAT
| |
| |
| |
| Вывод результата |
| Да |
| Нет |
| Ввод |
| Конец |

Рис.2. Алгоритм вычисления
1.2.1 Программа, составленная с присвоением значений переменным
20 d = 9 – a^2
30 IF d = 0 GOTO 60
40 END
50 PRINT (a^2 + 3 * b ^ 3 * c) – (5 * c / (9 – a^2))
60 PRINT "а не должно быть 3 или -3"
70 GOTO 10
1.2.2 Программа, работающая в диалоговом режиме
10 INPUT "Введите a,b,c"; a, b, c
20 d = 9 – a^2
30 IF d = 0 GOTO 60
40 END
50 PRINT (a^2 + 3 * b ^ 3 * c) – (5 * c / (9 – a^2))
60 PRINT "а не должно быть 3 или -3"
70 GOTO 10
Результат: 612,5555
Начало |
SHAPE \* MERGEFORMAT
| |
| |
| |
| Вывод результата |
| Да |
| Нет |
| Ввод |
| Конец |

Рис.3. Алгоритм вычисления
1.3.1 Программа, составленная с присвоением значений переменным
20 d = 8 – a^3
30 IF d = 0 GOTO 60
40 END
50 PRINT (5 * a^2 * b ^ 3 * c) + (3 * c^2 / (8 – a^3))
60 PRINT "а не должно быть 2 или -2"
70 GOTO 10
1.3.2. Программа, работающая в диалоговом режиме
10 INPUT "Введите a,b,c"; a, b, c
20 d = 8 – a^3
30 IF d = 0 GOTO 60
40 END
50 PRINT (5 * a^2 * b ^ 3 * c) + (3 * c^2 / (8 – a^3))
60 PRINT "а не должно быть 2 или -2"
70 GOTO 10
Результат: 34559,87
2. Решение задач
2.1 Матрицы и определители
2.1.1 Найти сумму двух матриц
| Начало |
| Конец |
| Ввод элементов матриц |
| |
| Вывод результата |
 | |||
 | |||
Рис.4. Алгоритм вычисления
Программа нахождения суммы двух матриц
CLS
PRINT BBЕDИTЕ(A)
INPUT "BBЕDИTЕ a11,a12,a13"; a11, a12, a13
INPUT "BBЕDИTЕ a21,a22,a23"; a21, a22, a23
INPUT "BBЕDИTЕ a31,a32,a33"; a31, a32, a33
CLS
PRINT BBЕDИTЕ(B)
INPUT "BBЕDИTЕ b11,b12,b13"; b11, b12, b13
INPUT "BBЕDИTЕ b21,b22,b23"; b21, b22, b23
INPUT "BBЕDИTЕ b31,b32,b33"; b31, b32, b33
CLS
PRINT a11 + b11; a12 + b12; a13 + b13
PRINT a21 + b21; a22 + b22; a23 + b23
PRINT a31 + b31; a32 + b32; a33 + b33
END
Результат:

2.1.2 Найти произведение двух матриц
| Ввод элементов матриц |
| Начало |
 | |||
| |
| Вывод результата |
| Конец |

Рис.5. Алгоритм вычисления
Программа нахождения произведения двух матриц
CLS
PRINT BBЕDИTЕ(A)
INPUT "BBЕDИTЕ a11,a12,a13"; a11, a12, a13
INPUT "BBЕDИTЕ a21,a22,a23"; a21, a22, a23
INPUT "BBЕDИTЕ a31,a32,a33"; a31, a32, a33
CLS
PRINT BBЕDИTЕ(B)
INPUT "BBЕDИTЕ b11,b12,b13"; b11, b12, b13
INPUT "BBЕDИTЕ b21,b22,b23"; b21, b22, b23
INPUT "BBЕDИTЕ b31,b32,b33"; b31, b32, b33
CLS
PRINT a11 * b11 + a12 * b21 + a13 * b31; a11 * b12 + a12 * b22 + a13 * b32; a11 * b13 + a12 * b23 + a13 * b33 PRINT a21 * b11 + a22 * b21 + a23 * b31; a21 * b12 + a22 * b22 + a23 * b32; a21 * b13 + a22 * b23 + a23 * b33 PRINT a31 * b11 + a32 * b21 + a33 * b31; a31 * b12 + a32 * b22 + a33 * b32; a31 * b13 + a32 * b23 + a33 * b33 END
Результат:

2.1.3 Вычислить определитель
| Ввод элементов матрицы |
| |
| Вывод результата |
| Конец |
| Начало |
 | |||||
 | |||||
Рис.6. Алгоритм вычисления
Программа вычисления определителя
PRINT BBЕDИTЕ(A)
INPUT "BBЕDИTЕ a1,b1,c1"; a1, b1, c1
INPUT "BBЕDИTЕ a2,b2,c2"; a2, b2, c2
INPUT "BBЕDИTЕ a3,b3,c3"; a3, b3, c3
PRINT a1 * b2 * c3 + b1 * c2 * a3 + a2 * b3 * c1 - a3 * b2 * c1 - b3 * c2 * a1 - a2 * b1 * c3
Результат: -163
2.1.4 Решить систему уравнений по формулам Крамера
| Ввод элементов матрицы |
| |
| Начало |
| Конец |
| Вывод результата |
 | |||||
 | |||||
Рис.7. Алгоритм вычисления
Программа решения системы уравнений по формулам Крамера
10 INPUT "BBЕDИTЕ KОЭФФИЦИЕHTЫ ПЕРВОГО УРАВНЕНИЯ"; a1, b1, c1, d1
20 INPUT "BBЕДИTЕ КОЭФФИЦИЕНТЫ ВТОРОГО УРАВНЕНИЯ"; a2, b2, c2, d2
30 INPUT "BBЕДИТЕ КОЭФФИЦИЕНТЫ ТРЕТЬЕГО УРАВНЕНИЯ"; a3, b3, c3, d3
40 d = a1 * b2 * c3 + b1 * c2 * a3 + a2 * b3 * c1 - a3 * b2 * c1 - b3 * c2 * a1 - a2 * b1 * c3
50 IF d = 0 GOTO 90
60 PRINT "x= "; (d1 * b2 * c3 + b1 * c2 * d3 + d2 * b3 * c1 - d3 * b2 * c1 - b3 * c2 * d1 - d2 * b1 * c3) / d
70 PRINT "y= "; (a1 * d2 * c3 + d1 * c2 * a3 + a2 * d3 * c1 - a3 * d2 * c1 - d3 * c2 * a1 - a2 * d1 * c3) / d
80 PRINT "z= "; (a1 * b2 * d3 + b1 * d2 * a3 + a2 * b3 * d1 - a3 * b2 * d1 - b3 * d2 * a1 - a2 * b1 * d3) / d
90 END
Результат: x=0,32; y=0,36; z=0,44
2.2 Основы векторного исчисления
Даны векторы
| Ввод координат векторов |
| |
| Начало |
| Конец |
| Вывод результата |
 | |||||
 | |||||
Рис.8. Алгоритм вычисления
Программа нахождения скалярного и векторного произведения векторов, угла между ними
INPUT "BBЕДИТЕ КООРДИНАТЫ ПЕРВОГО ВЕКТОРА"; x1, y1, z1
INPUT "BBЕДИТЕ КООРДИНАТЫ ВТОРОГО ВЕКТОРА "; x2, y2, z2
ska = x1 * x2 + y1 * y2 + z1 * z2
PRINT "СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ = "; ska
x3 = y1 * z2 - z1 * y2
y3 = x1 * z2 - z1 * x2
z3 = x1 * y2 - y1 * x2
PRINT "BEKTOPHOE ПPOUЗBEДEHИE a*b= "; x3, y3, z3
a = (x1 ^ 2 + y1 ^ 2 + z1 ^ 2) ^ (1 / 2)
b = (x2 ^ 2 + y2 ^ 2 + z2 ^ 2) ^ (1 / 2)
ugl = ska / (a * b)
PRINT "КОСИНУС УГЛА МЕЖДУ ВЕКТОРАМИ РАВЕН"; ugl
Результат: -14;
3. Графический режим Qbasic
3.1 Построение проекции
Задание. Найти объем пластины и построить ее проекции.
Программа выполнения
m = 71
L = 51
H = 8
R = 9
SCREEN 12
WINDOW (0, 0)-(120, 90)
LINE (90, 90)-(90, 0)
LINE (0, 30)-(120, 30)
LINE (90 - 1.1 * m, 30 + .1 * m)-(90 - .1 * m, 30 + .1 * m + L), , B
LINE (90 - 1.1 * m, 30 - .1 * m - H)-(90 - .1 * m, 30 - .1 * m), , B
LINE (90 + .1 * m, 30 + .1 * m)-(90 + .1 * m + H, 30 + .1 * m + L), , B
CIRCLE (90 - 1.1 * m + .1 * m + R, 30 + L - R), R
CIRCLE (90 - .1 * m - .1 * m - R, 30 + .1 * m + .1 * m + R), R
CIRCLE (90 - .1 * m - .1 * m - R, 30 + .1 * m + L - .1 * m - R), R
CIRCLE (90 - 1.1 * m + .1 * m + R, 30 + .2 * m + R), R PRINT " ОБЪЕМ РАВЕН"; m * L * H
3.2 Построение графиков функций
3.2.1 Построить график функции
Программа построения графика
SCREEN 12
WINDOW (-7, -6)-(7, 80)
X1 = -7: X2 = 4
H = (X2 - X1) / 100
Y1 = 3 * X1 ^ 2 + 8 * X1 + 3
PSET (X1, Y1)
FOR X = X1 TO X2 STEP H
Y = 3 * X ^ 2 + 8 * X + 3
LINE -(X, Y)
NEXT
3.2.2 Построить график функции
Программа построения графика
SCREEN 12
WINDOW (-1, -6)-(1, 40)
X1 = -2: X1 = 2
H = (X2 - X1) / 100
Y1 = 192 * X1 ^ 2 + 144 * X1 + 27
PSET (X1, Y1)
FOR X = X1 TO X2 STEP H
Y = 192 * X ^ 2 + 144 * X + 27
NEXT
3.2.3 Построить график функции
Программа построения графика
DEF FNA (X) = 3 / (8 * X + 3) ^ 2 SCREEN 12
WINDOW (-5, -5)-(5, 5)
X1 = -5: Y1 = FNA(X1)
X2 = -.4
X3 = -.3: Y3 = 27
X4 = 5
H = (X2 - X1) / 100
PSET (X1, Y1)
FOR X = X1 TO X2 STEP H
Y = FNA(X)
LINE -(X, Y)
NEXT
H = (X4 - X3) / 100
PSET (X3, Y3)
FOR X = X3 TO X4 STEP H
Y = FNA(X)
LINE -(X, Y)
NEXT
3.3 Геометрические преобразования
Выполнить последовательно геометрические преобразования:
- перенос;
- масштабирование;
- поворот относительно заданной точки.
Программа выполнения геометрических преобразований
SCREEN 12
WINDOW (-50, -10)-(20, 20)
X1 = -1
Y1 = 3
X2 = -9
Y2 = 1
DX = 1
DY = 3
SX = 5
SY = 3
LINE (X1, Y1)-(X2, Y2)'
LINE (X1 + DX, Y1 + DY)-(X2 + DX, Y2 + DY)'
LINE (X1 * SX, Y1 * SY)-(X2 * SX, Y2 * SY)'
LINE (8, 2)-(0, 0)
LINE ((X1 * COS(PI / 4) - Y1 * SIN(PI / 4)), (Y1 * SIN(PI / 4) + Y1 * COS(PI / 4)))-((0 * COS(PI / 4) - 0 * SIN(PI / 4)), (0 * SIN(PI / 4) + 0 * COS(PI / 4)))'
Выводы и заключение
Решение какой-либо задачи с помощью ЭВМ распадается на три основных этапа: постановка задачи, составление алгоритма решения, программная реализация алгоритма на ЭВМ. В данной работе реализованы все указанные выше этапы в среде программирования Qbasic.В работе представлены задания, направленные на овладение основами программирования в указанной среде: выполнение арифметических операций, решения задач из курса высшей математики, графические возможности.
В результате ее выполнения разработаны программы, охватывющие основные возможности версии, позволяющие выполнять все необходимые действия по составлению, отладке и выполнению программ.
В среде Qbasic существует несколько экранных режимов. Основной исходный экран представляет поле редактирования текста программы. Встроенный текстовый редактор выполняет две функции – редактирования текста и синхронной интерпретации строки. В этой связи строки в некоторых программах не нумеровались. Результаты работы программы, комментарии и сообщения интерпретатора представлялись в текстовом экране (по умолчанию режим SCREEN 0). При работе с графикой изображения строились в графическом экране, который имеет несколько режимов.
Особый интерес представляла система помощи help (подсказок), имеющая контекстную структуру с возможностью копирования примеров из текста подсказок, что позволило освоить работу с языком программирования Qbasic практически самостоятельно.
Таким образом, основная цель курсовой работы по овладению основами программирования в среде Qbasic выполнена.
Список литературы
1. Могилев А.В. Информатика. – М., 1999. – 816 с.
2. Сафронов И.К. Бейсик в задачах и примерах. –– СПб.: BHV, 2001. – 215 с.
3. Семашко Г.Л. Программирование для всех. – М.: Наука, 1986. – 325 с.
4. Ставнистый Н.Н. Qbasic в математике. Решение задач с помощью компьютера. Ч1. – М.: СОЛОН-Р, 2001. – 143 с.
5. Федоренко Ю. Алгоритмы и программы на QBASIC. - СПб.: Питер, 2002. – 287 с.
6. Хомоненко А.Д. Основы современных компьютерных технологий. – СПб.: КОРОНА принт, 1998. – 448 с.
7. Чернов Б.И. Программирование на алгоритмических языках Бейсик, Фортран, Паскаль. – М.: Просвещение, 1991. – 192 с.