Курсовая на тему Дослідження методів чисельного інтегрування
Работа добавлена на сайт bukvasha.net: 2014-12-12Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Міністерство освіти і науки України
2006
Анотація
В даній курсовій роботі розроблена програма для обчислення визначеного інтегралу методом Чебишева третього четвертого та п’ятого порядків.
Програма дозволяє отримати розв’язання інтегралу зазначеним методом, оцінити похибки та порівнювати їх з точним обчисленнями отриманими в математичному пакеті Mathcad 2001 Professional.
1. Теоретичні відомості
У курсовій роботі проведено дослідження методів чисельного інтегрування. Адже, у задачах, пов'язаних з аналізом, ідентифікацією, оцінкою якості, моделюванням різноманітних пристроїв автоматики, керування, інформаційно-вимірювальної техніки, радіоелектроніки, виникає необхідність обчислення визначених інтегралів.
В основу чисельного інтегрування покладено наближене обчислення площини під кривою, яка описується підінтегральною функцією інтеграла:
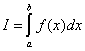
Загальний підхід до розв’язування цієї задачі такий: визначений інтеграл I являє собою площину, обмежену кривою f(х), віссю Х та прямими Х = a, Х =b, відрізок від a до b розбивають на множину менших відрізків, знаходять наближено площу кожної площини Si, яку отримують за таким розбиванням, значення інтеграла І знаходять як суму площ площин Sі, тобто I = 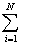
Si. При цьому використовують два способи розбивання початкового відрізка на менші
1.Розбивання відрізка проводиться раніше, до того ж завжди відрізок вибирають рівним (метод прямокутників, трапецій, Сімпсона).
2.Місцезнаходження та довжина відрізків визначаються аналізом, до того ж спочатку ставиться за мету досягти найбільшої точності з заданим числом відрізків, а потім відповідно з цим визначають їхні межі (методи Гаусса, Ньютона - Котеса, Чебишева) [1].
1.1 Метод прямокутників
Найпростішим методом наближеного обчислення інтеграла є метод прямокутників, геометрична інтерпретація якого зводиться до знаходження визначеного інтеграла як суми площ N прямокутників (з висотою f(x) та основою h= 
xi=xi+1-xi), отриманих розділень відрізка[a,b] на N рівних частин, до того ж якщо розділити на прямокутники зліва на право, то отримаємо формулу лівих прямокутників:
In= 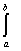
f(x)dx» 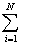
Si=h[f(x0)+f(x1)+...+f(xn-1)]= 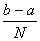
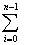
f(xi);(1.1)
якщо ж розділити на N прямокутників справа на ліво, то отримаємо формулу правих прямокутників:
Iпр= 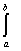
f(x)dx»h[f(xn)+...+f(x1)]= 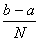
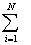
f(xi)(1.2)
1.2 Метод трапецій
Суть методу трапеції, полягає в тому, що інтеграл обчислюється по-іншому, відрізок інтегрування поділяється на N рівних відрізків, всередині яких підінтегральна крива f(x) замінюється кусково- лінійною функцією j(x), отриманою стягуванням ординат N відрізків хордами.
Обчислення визначеного інтеграла зводиться до знаходження сум площ Si прямокутних трапецій N.
Площа кожної такої трапеції визначається як:
Si=h 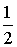
(f(xi)+f(xi+1)).(1.3)
Отже, формула трапеції:
I= 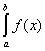
» 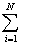
Si=h( 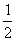
f(x0)+f(x1)+f(x2)+...+f(xn-1)+ 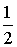
f(xN)= = 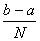
[ 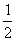
(f(x0)+f(xn))+ 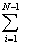
f(xi) 
]. 


(1.4)
Графічна модель

Похибка обчислення інтеграла за формулою трапецій оцінюється як
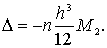
(1.5)
Де М2 –максимальне значення другої похідної. f(x) при 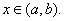
,h-крок обчислень.
1.3 Метод Сімпсона (метод парабол або метод криволінійних трапецій)
Цей метод також використано у курсовій роботі, близький до методу трапецій у тій частині, що інтегрування проводиться шляхом поділу відрізка інтегрування [а, b] на множину відрізків (N пар відрізків). Однак, з метою збільшення точності наближеного інтегрування на кожному відрізку [Xi, Xi+2] підінтегральної функції f(x) замінюють квадратичною параболою j(x), обчислення визначеного інтеграла зводиться до обчислення суми N криволінійних трапецій Si: I= 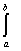
f(x)dx» 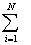
Si [1].
Графічна модель.
Площа кожної такої трапеції визначається за формулою Сімпсона:
Si= 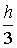
[f(xi)+4f ( 
xi+1)+f(xi+2)], (1.6), тобто
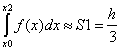
(y0+4y1+y2),
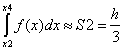
(y2+4y3+y4),
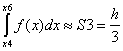
(y4+4y5+y6), (1.7)
. . . . . . . . . . . . . . . . . . . . . . .
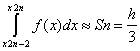
(y2n-2+4y2n-1+y2n),
Тоді чисельне значення визначеного інтеграла на відрізку [a,b] дорівнюватиме сумі інтегралів, тобто
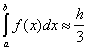
[y0+y2n+4(y1+...+y2n-1)+2(y2+...+y2n-2)],
або
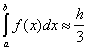
[y0+y2n+4 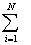
y2i-1+2 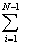
y2i],(1.8)
де h =(b-a)/2N.
Похибка обчислення інтеграла за формулою Сімпсона оцінюється як
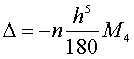
де М4 –максимальне значення четвертої похідної. f(x) при 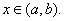
, h-крок обчислень.
1.4 Метод Ньютона-Котеса
Цей метод засновано на апроксимації однієї із сторін криволінійної трапеції, яка отримується поділом відрізка [a,b] на N рівних частин, многочленами вищих порядків, також як у методі трапецій використовується лінійна апроксимація (заміна однієї із сторін трапеції прямою лінією), а в методі Сімпсона - апроксимація параболою.
Основна формула методу:
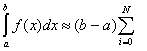
yiHi,(1.9)
де Hi - коефіцієнти Ньютона - Котеса. Ці коефіцієнти не залежать від вигляду f(x), а є функцією тільки N (кількість вузлів інтерполяцїї). Таким чином, коефіцієнти Ньютона - Котеса можна обчислити раніше для різного числа вузлів інтерполяції .
Легко можна показати, що методи трапецій та Сімпсона є частинними випадками методу Ньютона - Котеса.
1.5 Метод Чебишева
Метод Чебишева використано в курсовій грунтується на обчисленні інтеграла за значеннями функції yi =f(xi),(i=1,2,...,N) у зафіксованих вузлах інтерполяції x1,x2,...,xN (де h=const). Коефіцієнти Ньютона -Котеса Нi (i=1,N) не залежать від значень функції у вузлах інтерполяції. П.Л.Чебишев запропонував для обчислення визначених інтегралів використати формулу:
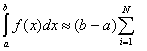
cif(xi),(1.10)
в якій квадратурні коефіцієнти сi (i = 1,2, ...,N) зафіксовані, а абсциси xi (i=1,2,...,N)підлягаютьвизначенню.
Таблиця 1.1.
Коефіцієнти Ньютона - Котеса
Для простоти обчислень необхідно вибрати С1=...=Сn. Розглядаємо спочатку частинний випадок, коли межі інтегрування дорівнюють -1 та 1. Тоді формула Чебишева набере вигляду:
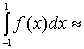
2Cn[f(x1)+f(x2)+...+f(xn)],(1.11)
де квадратурні коефіцієнти Сn та абсциси xi підлягають визначенню.
Коефіцієнти та вузли інтерполяції xi визначимо із умови, що ця рівність є точною для випадку, коли f(х) многочлен вигляду:
f(x)=a0+a1x+a2x2+...+anxn.(1.12)
Підставимо многочлен у ліву частину попередньої формули та про- інтегруємо:
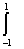
(a0+a1x+a2x2+...+anxn)=2(a0+ 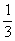
a2+ 
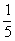
a3+...).(1.13)
У праву частину рівності (1. 11) підставимо значення многочлена (1.І2) у вузлах x1,x2,...,xn:
f(x1)=a0+a1x1+a2x12+a3x13+...+anx1n,
f(x2)=a0+a1x2+a2x22+a3x23+...+anx2n,
f(x3)=a0+a1x3+a2x32+a3x33+...+anx3n,(1.14)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
f(xn)=a0+a1xn+a2xn2+a3xn3+...+anxnn,
Тоді рівність (1.ІЗ) набере вигляду:
2(a0+ 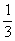
a2+ 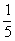
a4+...)=2cn[na0+a1(x1+x2+...+xn)+a2(x12+x22+...+xn2)+
+a3(x13+x23+...+xn3)+...+an(x1n+x2n+...+xnn)].(1.15)
Отримана рівність повинна виконуватися за будь-яких значень a0,a1,...,an; таким чином, порівнюючи коефіцієнти аi в правій та лівій частинах (1.І5) знаходимо, що nсn = 1, звідки
Cn= 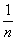
.(1.16)
і, крім цього,
x1+x2+x3+...+xn=0,
x12+x22+x32+...+xn2= 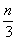
,
x13+x23+x33+...+xn3=0,(1.17)
x14+x24+x34+...+xn4= 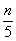
,
. . . . . . . . . . . . . . . . . . .
x1n+x2n+x3n+...+xnn= 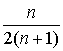
[1-(-1)n+1],
Підставляючи знайдене для Сn виразу в співвідношені 1.13 отримаємо формулу Чебишева:
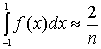
[f(x1)+f(x2)+...+f(xn)],(1.18)
де точки x1,...,хn визначаються із системи рівнянь (1.17).
Значення x1,...,хn для різних n обчислюються раніше та зводять в табл. 1.2.
Коли межі даного інтеграла відрізняються від -1 та 1, формула Чебишева матиме вигляд:
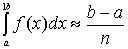
[f(z1)+f(z2)+...+f(zn)],(1.19)
де
Таблиця 1.2.
Zi= 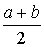
+ 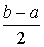
xi, (i=1,2,...,n),(1.20)
а xi мають вкaзані в таблиці значення.
Похибка обчислень за методом Чебишева знаходиться за формулою:
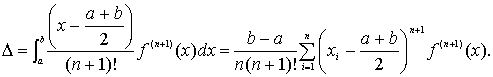
При запуску спершу ініціюється графіка та створюється меню і ініціюються змінні. Потім іде блок зчитування з клавіатури. Він аналізує введену користувачем інформацію і згідно з нею виконує певні дії. При натисканні на клавіші управління курсором відбувається переміщення по меню. При натисканні на клавішу Enter відбувається аналіз кнопки, яка була обрана на даний момент, і згідно з цим виконання певних дій. Це можуть бути такі операції:
1) обчислення інтегралу методом Чебишева 3-го порядку: виконується алгоритм, який детально пояснено в додатку Б.
2) обчислення інтегралу методом Чебишева 4-го порядку.
3) обчислення інтегралу методом Чебишева 5-го порядку
4) Задається крок обчислення h=0.1;
5) Задається крок обчислення h=0.2;
6) Задається крок обчислення h=0.5;
7) Про автора – довідка про автора програми;
8) Вихід з програми – здійснюється вихід з програмного середовища ТР;
Робота даної програми починається з підключення стандартного модуля введення-виведення crt та модуля graph для ініціалізації графіки, оскільки програма виконана в графічному режимі. Далі задаються константи інтегрування.
Тип TMenuItems – масив пунктів меню. Далі задаємо підінтегральну функцію. Процедура InitGraphMode – процедура для ініціалізації графіки, VGA - тип графічного драйверу, VGAHi – тип графічного режиму.
· DrawCursor(x,y:integer) – процедура для малювання курсору;
· HideCursor(x,y:integer) – процедура, що автоматично забирає курсор з екрану;
· Function WaitWhileKeydivssed(var FKey:boolean):char – функція, що очікує нажатої клавіші, цикл повторюється до тих пір, доки не буде зчитано код нажатої клавіші;
· Procedure menu(x,y:integer;…var poin:integer) – дана процедура власне виводить на екран графічне меню та надає змогу користувачеві здійснити вибір пункту меню за допомогою графічного курсору.
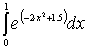
, методом Чебишева третього, четвертого та п’ятого порядків, також дає змогу зменшити похибку обчислень за рахунок зменшення кроку інтегрування.
Програма має гарний інтерфейс користувача з меню, що керується з клавіатури. Результати обчислень виводяться на екран монітора.
Дана програма пристосована для вирішення тільки одного інтегралу, а тому є вузько спеціалізованою, проте можлива зміна підінтегральної функції шляхом корегування програмного коду.
Комп'ютер може швидко опрацьовувати дані і виводити результати на екран.
4. Вхідні та вихідні дані
Вхідні дані:
1. Інтеграл: I= 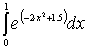
;
2. Крок обчислень 0.1,0.2,0.5;
3. Порядок інтегрування: третього , четвертого та п’ятого порядку.
Вихідні дані:
1. Значення інтегралу, що знаходить программа.
2. Загальна похибка по заданим методам.
3. Порівняння результатів з точним значенням.
5. Результати розрахунків
Результатами обчислень є знаходження значення визначеного інтеграла I= 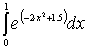
, , зазначеними методами, з кроком: h=0.1, h=0.2, h=0.5.
При розрахунку інтегралу 3-го порядку програма виведе на екран слідуючі результати:
Інтеграл Чебишева 3-го порядку: 2.649061117170
Загальна похибка: 0.0316342854
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.5
Інтеграл Чебишева 3-го порядку: 2,66138784520
Загальна похибка: 0.0193076119
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.2
Інтеграл Чебишева 3-го порядку: 2,67298758310
Загальна похибка: 0.00770787
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.1
При розрахунку інтегралу 4-го порядку програма виведе на екран слідуючі результати:
Інтеграл Чебишева 4-го порядку: 2.6680680931
Загальна похибка: 0.01262744
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.5
Інтеграл Чебишева 4-го порядку: 2,6743859370
Загальна похибка: 0.006309519
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.2
Інтеграл Чебишева 4-го порядку: 2,676438956720
Загальна похибка: 0,00385156152
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.1
При розрахунку інтегралу 5-го порядку програма виведе на екран слідуючі результати:
Інтеграл Чебишева 5-го порядку: 2,68069554160
Загальна похибка: 0.00000008443
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.5
Інтеграл Чебишева 5-го порядку: 2.68069545713707
Загальна похибка: 0.00000000512
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.2
Інтеграл Чебишева 5-го порядку: 2.68069545714209
Загальна похибка: 0,00000000010
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.1
Висновки
В даній курсовій роботі було проведене дослідження чисельних методів вирішення визначеного інтегралу виду I= 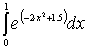
, по методу Чебишева.
Алгоритм методу є досить простим. Для його реалізації потрібно мати функцію, межі та крок інтегрування.
В курсовій роботі, для перевірки результатів обчислень, я використовував математичний пакет MatchCad 2001. Похибку для даної функції доцільно було б оцінювати, як абсолютне значення різниці між точним значенням та одержаним в програмі.
Однак, хоча й виникали певні труднощі з виконанням завдання, але це було безперечно цікаво, і багато чому мене навчили.
Література
1. В.Т.Маликов, Р.Н.Кветный. Вычислительные методы и применение ЭВМ. – К.: Вища школа, 1989.– 213 с.
2. В.М. Дубовий, Р.Н.Квєтний Методичні вказівки до лабораторних робіт з програмування та застосування ЕОМ . Навчальне видання. –Вінниця, ВПІ, 1992.
3. В.М. Дубовий, Р.Н.Квєтний. Програмування комп’ютеризованих систем управління та автоматики. - В.: ВДТУ, 1997. – 208с.
4. Р.Н.Кветний Методи комп’ютерних обчислень. Навчальний посібник.- Вінниця: ВДТУ, 2001.-148с.
5. А. І. Марченко, Л. А. Марченко “Программирование в среде Турбо Паскаль 7.0”, Київ “ВЕК+”, 1999 р.
Вінницький національний технічний університет
Інститут автоматики, електроніки та комп’ютерних
систем управління
Факультет АКСУ
Кафедра АІВТ
Курсова робота
з дисципліни
«Обчислювальні методи та застосування ЕОМ»
Дослідження методів чисельного інтегрування2006
Анотація
В даній курсовій роботі розроблена програма для обчислення визначеного інтегралу методом Чебишева третього четвертого та п’ятого порядків.
Програма дозволяє отримати розв’язання інтегралу зазначеним методом, оцінити похибки та порівнювати їх з точним обчисленнями отриманими в математичному пакеті Mathcad 2001 Professional.
1. Теоретичні відомості
У курсовій роботі проведено дослідження методів чисельного інтегрування. Адже, у задачах, пов'язаних з аналізом, ідентифікацією, оцінкою якості, моделюванням різноманітних пристроїв автоматики, керування, інформаційно-вимірювальної техніки, радіоелектроніки, виникає необхідність обчислення визначених інтегралів.
В основу чисельного інтегрування покладено наближене обчислення площини під кривою, яка описується підінтегральною функцією інтеграла:
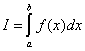
Загальний підхід до розв’язування цієї задачі такий: визначений інтеграл I являє собою площину, обмежену кривою f(х), віссю Х та прямими Х = a, Х =b, відрізок від a до b розбивають на множину менших відрізків, знаходять наближено площу кожної площини Si, яку отримують за таким розбиванням, значення інтеграла І знаходять як суму площ площин Sі, тобто I =
1.Розбивання відрізка проводиться раніше, до того ж завжди відрізок вибирають рівним (метод прямокутників, трапецій, Сімпсона).
2.Місцезнаходження та довжина відрізків визначаються аналізом, до того ж спочатку ставиться за мету досягти найбільшої точності з заданим числом відрізків, а потім відповідно з цим визначають їхні межі (методи Гаусса, Ньютона - Котеса, Чебишева) [1].
1.1 Метод прямокутників
Найпростішим методом наближеного обчислення інтеграла є метод прямокутників, геометрична інтерпретація якого зводиться до знаходження визначеного інтеграла як суми площ N прямокутників (з висотою f(x) та основою h=
In=
якщо ж розділити на N прямокутників справа на ліво, то отримаємо формулу правих прямокутників:
Iпр=
1.2 Метод трапецій
Суть методу трапеції, полягає в тому, що інтеграл обчислюється по-іншому, відрізок інтегрування поділяється на N рівних відрізків, всередині яких підінтегральна крива f(x) замінюється кусково- лінійною функцією j(x), отриманою стягуванням ординат N відрізків хордами.
Обчислення визначеного інтеграла зводиться до знаходження сум площ Si прямокутних трапецій N.
Площа кожної такої трапеції визначається як:
Si=h
Отже, формула трапеції:
I=
Графічна модель

Похибка обчислення інтеграла за формулою трапецій оцінюється як
Де М2 –максимальне значення другої похідної. f(x) при
1.3 Метод Сімпсона (метод парабол або метод криволінійних трапецій)
Цей метод також використано у курсовій роботі, близький до методу трапецій у тій частині, що інтегрування проводиться шляхом поділу відрізка інтегрування [а, b] на множину відрізків (N пар відрізків). Однак, з метою збільшення точності наближеного інтегрування на кожному відрізку [Xi, Xi+2] підінтегральної функції f(x) замінюють квадратичною параболою j(x), обчислення визначеного інтеграла зводиться до обчислення суми N криволінійних трапецій Si: I=
 |
Графічна модель.
Площа кожної такої трапеції визначається за формулою Сімпсона:
Si=
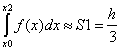
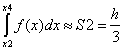
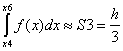
. . . . . . . . . . . . . . . . . . . . . . .
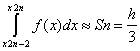
Тоді чисельне значення визначеного інтеграла на відрізку [a,b] дорівнюватиме сумі інтегралів, тобто
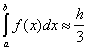
або
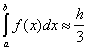
де h =(b-a)/2N.
Похибка обчислення інтеграла за формулою Сімпсона оцінюється як
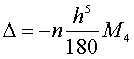
де М4 –максимальне значення четвертої похідної. f(x) при
1.4 Метод Ньютона-Котеса
Цей метод засновано на апроксимації однієї із сторін криволінійної трапеції, яка отримується поділом відрізка [a,b] на N рівних частин, многочленами вищих порядків, також як у методі трапецій використовується лінійна апроксимація (заміна однієї із сторін трапеції прямою лінією), а в методі Сімпсона - апроксимація параболою.
Основна формула методу:
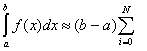
де Hi - коефіцієнти Ньютона - Котеса. Ці коефіцієнти не залежать від вигляду f(x), а є функцією тільки N (кількість вузлів інтерполяцїї). Таким чином, коефіцієнти Ньютона - Котеса можна обчислити раніше для різного числа вузлів інтерполяції .
Легко можна показати, що методи трапецій та Сімпсона є частинними випадками методу Ньютона - Котеса.
1.5 Метод Чебишева
Метод Чебишева використано в курсовій грунтується на обчисленні інтеграла за значеннями функції yi =f(xi),(i=1,2,...,N) у зафіксованих вузлах інтерполяції x1,x2,...,xN (де h=const). Коефіцієнти Ньютона -Котеса Нi (i=1,N) не залежать від значень функції у вузлах інтерполяції. П.Л.Чебишев запропонував для обчислення визначених інтегралів використати формулу:
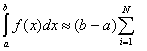
в якій квадратурні коефіцієнти сi (i = 1,2, ...,N) зафіксовані, а абсциси xi (i=1,2,...,N)підлягаютьвизначенню.
Таблиця 1.1.
Коефіцієнти Ньютона - Котеса
| n = 1 | Но = H1 = ½ | |
| n = 2 | Но = Н2 = 1/6, Н1 = 2/3 | |
| n = 3 | Н0 = Н3 = 1/8, Н1 = H2 = 3/8 | |
| n = 4 | Но = Н4 = 7/90, Н1 = Нз = 16/45, Н2 = 2/15 | |
| n = 5 | Н0 = Н5 =19/288, Н1 = Н4 = 25/96, Н2 = Нз = = 25/144 | |
| n = 6 | Но = Н6 = 41/840, Н1 = Н5 = 9/35, Н2 = Н4 = =9/280, Нз = 34/105 | |
| n = 7 | Но = Н7 = 75І/17280, Н1 = Н6 = 3577/1728О, Н2 = Н5 =1323/1728О, Нз = Н4 = 2989/17280 | |
де квадратурні коефіцієнти Сn та абсциси xi підлягають визначенню.
Коефіцієнти та вузли інтерполяції xi визначимо із умови, що ця рівність є точною для випадку, коли f(х) многочлен вигляду:
f(x)=a0+a1x+a2x2+...+anxn.(1.12)
Підставимо многочлен у ліву частину попередньої формули та про- інтегруємо:
У праву частину рівності (1. 11) підставимо значення многочлена (1.І2) у вузлах x1,x2,...,xn:
f(x1)=a0+a1x1+a2x12+a3x13+...+anx1n,
f(x2)=a0+a1x2+a2x22+a3x23+...+anx2n,
f(x3)=a0+a1x3+a2x32+a3x33+...+anx3n,(1.14)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
f(xn)=a0+a1xn+a2xn2+a3xn3+...+anxnn,
Тоді рівність (1.ІЗ) набере вигляду:
2(a0+
+a3(x13+x23+...+xn3)+...+an(x1n+x2n+...+xnn)].(1.15)
Отримана рівність повинна виконуватися за будь-яких значень a0,a1,...,an; таким чином, порівнюючи коефіцієнти аi в правій та лівій частинах (1.І5) знаходимо, що nсn = 1, звідки
Cn=
і, крім цього,
x1+x2+x3+...+xn=0,
x12+x22+x32+...+xn2=
x13+x23+x33+...+xn3=0,(1.17)
x14+x24+x34+...+xn4=
. . . . . . . . . . . . . . . . . . .
x1n+x2n+x3n+...+xnn=
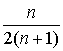
Підставляючи знайдене для Сn виразу в співвідношені 1.13 отримаємо формулу Чебишева:
де точки x1,...,хn визначаються із системи рівнянь (1.17).
Значення x1,...,хn для різних n обчислюються раніше та зводять в табл. 1.2.
Коли межі даного інтеграла відрізняються від -1 та 1, формула Чебишева матиме вигляд:
де
Таблиця 1.2.
| Число ординат | Значення абсцис |
| n = 2 n = 3 n = 4 n = 5 n = 6 n = 7 | -x1 = x2 = 0.577350 -x1 = x3 = 0.707107; x2 = 0 -x1 = x4 = 0.794654; -x2 = x3 = 0.187592 -x1 = x5 = 0.832498; -x2 = x4 = 0.374541; х3 = 0 -x1 = x6 = 0.866247; -x2 = x5 = 0.4225І9; -x3 = x4 = 0.266635 -x1 = x7 = 0.883862; -x2 = x6 = 0.529657; -x3= = x5 = 0.323912; x4 = 0 |
а xi мають вкaзані в таблиці значення.
Похибка обчислень за методом Чебишева знаходиться за формулою:
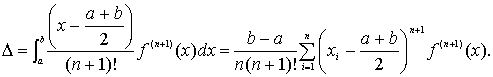
2. Розробка та опис логічної частини програми
Програма складається з двох блоків. Це – інтерфейний модуль, що забезпечує користувача змогою спілкуватися з комп’ютером за допомогою клавіатури, та сама програма, що здійснює всі обчислювальні операції.При запуску спершу ініціюється графіка та створюється меню і ініціюються змінні. Потім іде блок зчитування з клавіатури. Він аналізує введену користувачем інформацію і згідно з нею виконує певні дії. При натисканні на клавіші управління курсором відбувається переміщення по меню. При натисканні на клавішу Enter відбувається аналіз кнопки, яка була обрана на даний момент, і згідно з цим виконання певних дій. Це можуть бути такі операції:
1) обчислення інтегралу методом Чебишева 3-го порядку: виконується алгоритм, який детально пояснено в додатку Б.
2) обчислення інтегралу методом Чебишева 4-го порядку.
3) обчислення інтегралу методом Чебишева 5-го порядку
4) Задається крок обчислення h=0.1;
5) Задається крок обчислення h=0.2;
6) Задається крок обчислення h=0.5;
7) Про автора – довідка про автора програми;
8) Вихід з програми – здійснюється вихід з програмного середовища ТР;
Робота даної програми починається з підключення стандартного модуля введення-виведення crt та модуля graph для ініціалізації графіки, оскільки програма виконана в графічному режимі. Далі задаються константи інтегрування.
Тип TMenuItems – масив пунктів меню. Далі задаємо підінтегральну функцію. Процедура InitGraphMode – процедура для ініціалізації графіки, VGA - тип графічного драйверу, VGAHi – тип графічного режиму.
· DrawCursor(x,y:integer) – процедура для малювання курсору;
· HideCursor(x,y:integer) – процедура, що автоматично забирає курсор з екрану;
· Function WaitWhileKeydivssed(var FKey:boolean):char – функція, що очікує нажатої клавіші, цикл повторюється до тих пір, доки не буде зчитано код нажатої клавіші;
· Procedure menu(x,y:integer;…var poin:integer) – дана процедура власне виводить на екран графічне меню та надає змогу користувачеві здійснити вибір пункту меню за допомогою графічного курсору.
3. Функціональне призначення програми
Програма призначена для обчислення визначеного інтегралу I=Програма має гарний інтерфейс користувача з меню, що керується з клавіатури. Результати обчислень виводяться на екран монітора.
Дана програма пристосована для вирішення тільки одного інтегралу, а тому є вузько спеціалізованою, проте можлива зміна підінтегральної функції шляхом корегування програмного коду.
Комп'ютер може швидко опрацьовувати дані і виводити результати на екран.
4. Вхідні та вихідні дані
Вхідні дані:
1. Інтеграл: I=
2. Крок обчислень 0.1,0.2,0.5;
3. Порядок інтегрування: третього , четвертого та п’ятого порядку.
Вихідні дані:
1. Значення інтегралу, що знаходить программа.
2. Загальна похибка по заданим методам.
3. Порівняння результатів з точним значенням.
5. Результати розрахунків
Результатами обчислень є знаходження значення визначеного інтеграла I=
При розрахунку інтегралу 3-го порядку програма виведе на екран слідуючі результати:
Інтеграл Чебишева 3-го порядку: 2.649061117170
Загальна похибка: 0.0316342854
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.5
Інтеграл Чебишева 3-го порядку: 2,66138784520
Загальна похибка: 0.0193076119
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.2
Інтеграл Чебишева 3-го порядку: 2,67298758310
Загальна похибка: 0.00770787
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.1
При розрахунку інтегралу 4-го порядку програма виведе на екран слідуючі результати:
Інтеграл Чебишева 4-го порядку: 2.6680680931
Загальна похибка: 0.01262744
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.5
Інтеграл Чебишева 4-го порядку: 2,6743859370
Загальна похибка: 0.006309519
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.2
Інтеграл Чебишева 4-го порядку: 2,676438956720
Загальна похибка: 0,00385156152
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.1
При розрахунку інтегралу 5-го порядку програма виведе на екран слідуючі результати:
Інтеграл Чебишева 5-го порядку: 2,68069554160
Загальна похибка: 0.00000008443
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.5
Інтеграл Чебишева 5-го порядку: 2.68069545713707
Загальна похибка: 0.00000000512
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.2
Інтеграл Чебишева 5-го порядку: 2.68069545714209
Загальна похибка: 0,00000000010
Точне розв’язання (Mathcad 2001): 2.68069545714219
Крок: 0.1
Висновки
В даній курсовій роботі було проведене дослідження чисельних методів вирішення визначеного інтегралу виду I=
Алгоритм методу є досить простим. Для його реалізації потрібно мати функцію, межі та крок інтегрування.
В курсовій роботі, для перевірки результатів обчислень, я використовував математичний пакет MatchCad 2001. Похибку для даної функції доцільно було б оцінювати, як абсолютне значення різниці між точним значенням та одержаним в програмі.
Однак, хоча й виникали певні труднощі з виконанням завдання, але це було безперечно цікаво, і багато чому мене навчили.
Література
1. В.Т.Маликов, Р.Н.Кветный. Вычислительные методы и применение ЭВМ. – К.: Вища школа, 1989.– 213 с.
2. В.М. Дубовий, Р.Н.Квєтний Методичні вказівки до лабораторних робіт з програмування та застосування ЕОМ . Навчальне видання. –Вінниця, ВПІ, 1992.
3. В.М. Дубовий, Р.Н.Квєтний. Програмування комп’ютеризованих систем управління та автоматики. - В.: ВДТУ, 1997. – 208с.
4. Р.Н.Кветний Методи комп’ютерних обчислень. Навчальний посібник.- Вінниця: ВДТУ, 2001.-148с.
5. А. І. Марченко, Л. А. Марченко “Программирование в среде Турбо Паскаль 7.0”, Київ “ВЕК+”, 1999 р.
Додаток А
Лістинг
program Kursova;
uses crt,graph;
const
a=0;
b=1;
c=1.5;
d=2;
t3:array[1..3] of real=(-0.707107,0,0.707107);
t4:array[1..4] of real=(-0.794654,-0.187592,0.187592,0.794654);
t5:array[1..5] of real=(-0.832498,-0.374541,0,0.374541,0.832498);
Type TMenuItems=array[1..10] of string;
TDelta=array[1..300] of real;
Var Item:TMenuItems;
ResM:TDelta;
i,n:integer;
h:real;
ki:integer;
M,x,Ic,I2n,nc,sc1,sc2,I1n,x1,x2:real;
s,hs,s1:string;
k:Integer;
sum,int,si:real;
Delta,AllDelta,sum1:real;
Function Fact(n:integer):integer;
begin
if n=0 then Fact:=1
else Fact:=n*Fact(n-1)
end;
{Ф-я}
function f(x1:real):real;
begin
f:=exp(-d*x1*x1+c)
end;
procedure InitGraphMode;
var gd,gm:integer;
begin
gd:=VGA;
gm:=VGAHi;
initgraph(gd,gm,'');
end;
procedure DrawCursor(x,y:integer);
var i,j:integer;
begin
setcolor(white);
setlinestyle(0,0,1);
MoveTo(x,y+3);LineTo(x+10+5,y);LineTo(x+5,y-10);LineTo(x+10+10+5,y+3);
LineTo(x+5,y+16);LineTo(x+10+5,y+6);LineTo(x,y+3);
setfillstyle(1,red);
end;
{---------------------------------------------------------------------------}
Procedure HideCursor(x,y:integer);
begin
setcolor(lightblue); {insert your background color instead of black}
setlinestyle(0,0,1);
MoveTo(x,y+3);LineTo(x+10+5,y);LineTo(x+5,y-10);LineTo(x+10+10+5,y+3);
LineTo(x+5,y+16);LineTo(x+10+5,y+6);LineTo(x,y+3);
setfillstyle(1,red);
end;
Function WaitWhileKeydivssed(var FKey:boolean):char;
var result:char;
begin
FKey:=false;
while keydivssed do result:=readkey; {It clears keyboard buffer}
repeat until keydivssed;
result:=readkey;
if result=#0 then
begin
result:=readkey;
FKey:=true;
end;
WaitWhileKeydivssed:=result;
end;
Procedure Menu(x,y:integer;Items:TMenuItems;n:integer;var point:integer);
var i:integer;
ch:char;
FKey:boolean;
begin
setbkcolor(lightblue);
setcolor(yellow);
Rectangle(10,10,625,465);
setcolor(lightgreen);
Rectangle(14,14,621,461);
setcolor(lightred);
for i:=1 to n do outtextxy(x+50,y+(i-1)*30,Items[i]);
repeat
for i:=1 to n do
if i<>point then HideCursor(x,y+(i-1)*30)
else DrawCursor(x,y+(i-1)*30);
ch:=WaitWhileKeydivssed(FKey);
case ch of
#72: if point>1 then dec(point);
#80: if point<n then inc(point);
#27: point:=-1;
end;
until (ch=#13) or (ch=#27);
for i:=1 to n do HideCursor(x,y+(i-1)*30);
end;
procedure PrintArray(n:integer; m:TDelta);
var s0,s1:string;
begin
setfillstyle(1,lightblue);
bar(360,40,620,450);
for i:=1 to n do
begin
str(i,s0);
str(m[i]:5:10,s1);
if (i mod 25 =0) then
begin
readln;
bar(360,40,620,450);
end;
outtextxy(430,(i mod 25)*15+40,s0+' '+s1);
end;
end;
{-----------------------------------------------------------------------}
begin
InitGraphMode;
setcolor(blue);
h:=0.1;
repeat
cleardevice;
Item[1]:='Метод Чебишева 3-го порядку';
Item[2]:='Метод Чебишева 4-го порядку';
Item[3]:='Метод Чебишева 5-го порядку';
Item[4]:='Крок обчислень=0.1';
Item[5]:='Крок обчислень=0.2';
Item[6]:='Крок обчислень=0.5';
Item[7]:='Про автора';
Item[8]:='Вихид';
i:=1;
setcolor(white);
Menu(50,30,Item,7,i);
case i of
1:begin
setbkcolor(lightblue);x:=a; sum:=0; i:=0;
while x<=b do begin
inc(i);
x:=x+h;
si:=0;
for k:=1 to 3 do si:=si+f(x-h/2+h/2*t3[k]);
si:=h/3*si;
sum:=sum+si;
sum1:=(x-((a+b)/2))*(x-((a+b)/2))*(x-((a+b)/2))*(x-((a+b)/2))*
48*exp(-2*x*x+1.5)-384*x*x*exp(-2*x*x+1.5)+256*x*x*x*x*exp(-2*x*x+1.5);
n:=i+10;
end;
delta:=((b-a)/(n*fact(3)))*sum1;
delta:=Abs(delta);
AllDelta:=abs(delta);
str(Delta:12:10,s1);
Resm[i]:=Delta;
setcolor(red);
str(Sum:12:18,s);
str(AllDelta:12:20,s1);
str(h:2:3,hs);
setcolor(blue);
Outtextxy(100,240,'Интеграл: '+s);
Outtextxy(45,260,'Точне значення (Mathcad): 2.68069545714219');
Outtextxy(100,280,'Похибка: '+s1);
Outtextxy(100,300,'Крок: '+hs);
readln;
end;
2: begin
setbkcolor(lightblue);x:=a; sum:=0; i:=0;
while x<=b do begin
inc(i);
x:=x+h;
si:=0;
for k:=1 to 4 do si:=si+f(x-h/2+h/2*t4[k]);
si:=h/4*si;
sum:=sum+si;
sum1:=(x-((a+b)/2))*(x-((a+b)/2))*(x-((a+b)/2))*(x-((a+b)/2))*(x-((a+b)/2))*
(-960*x*exp(-2*x*x+1.5)+2560*x*x*x*exp(-2*x*x+1.5)-1024*x*x*x*x*x*exp(-2*x*x+1.5));
n:=i+10;
end;
delta:=((b-a)/(n*fact(3)))*sum1;
delta:=Abs(delta);
AllDelta:=abs(delta);
str(Delta:12:10,s1);
Resm[i]:=Delta;
setcolor(red);
str(Sum:12:18,s);
str(AllDelta:12:20,s1);
str(h:2:3,hs);
setcolor(blue);
Outtextxy(100,240,'Интеграл: '+s);
Outtextxy(45,260,'Точне значення (Mathcad): 2.68069545714219');
Outtextxy(100,280,'Похибка: '+s1);
Outtextxy(100,300,'Крок: '+hs);
readln;
end;
3:begin
setbkcolor(lightblue);x:=a; sum:=0; i:=0;
while x<=b do begin
inc(i);
x:=x+h;
si:=0;
for k:=1 to 5 do si:=si+f(x-h/2+h/2*t5[k]);
si:=h/5*si;
sum:=sum+si;
sum1:=(x-((a+b)/2))*(x-((a+b)/2))*(x-((a+b)/2))*(x-((a+b)/2))*(x-((a+b)/2))*
(x-((a+b)/2))*(-960*exp(-2*x*x+1.5)+11520*x*x*exp(-2*x*x+1.5)
-15360*x*x*x*x*exp(-2*x*x+1.5)+4096*x*x*x*x*x*x*exp(-2*x*x+1.5));
n:=i+10;
end;
delta:=((b-a)/(n*fact(3)))*sum1;
delta:=Abs(delta);
AllDelta:=abs(delta);
str(Delta:12:10,s1);
Resm[i]:=Delta;
setcolor(red);
str(Sum:12:18,s);
str(AllDelta:12:20,s1);
str(h:2:3,hs);
setcolor(blue);
Outtextxy(100,240,'Интеграл: '+s);
Outtextxy(45,260,'Точне значення (Mathcad): 2.68069545714219');
Outtextxy(100,280,'Похибка: '+s1);
Outtextxy(100,300,'Крок: '+hs);
readln;
end;
4: begin
sound(500);
setbkcolor(lightred);
h:=0.01;
Outtextxy(150,200,'Крок h=0.01 ');
Outtextxy(170,250,'Натиснить будь-яку клавишу ...');
delay(10000);
nosound;
repeat until keydivssed;
end;
5: begin
setbkcolor(lightred);
h:=0.02;
Outtextxy(150,200,'Крок h=0.02 ');
Outtextxy(170,250,'Натиснить будь-яку клавишу ...');
repeat until keydivssed;
end;
6: begin
setbkcolor(lightred);
h:=0.05;
Outtextxy(150,200,'Крок h=0.05 ');
Outtextxy(170,250,'Натиснить будь-яку клавишу ...');
repeat until keydivssed;
end;
7: begin
setbkcolor(lightred);
Outtextxy(160,200,'Програму виконав ст.гр. 3АВ-02');
Outtextxy(210,220,'Нетяга О.В.');
repeat until keydivssed;
end;
8: exit;
end;
until (i=7) or (i=-1);
CloseGraph;
end.
Додаток Б
| Задання початкових умов: x:=a; sum:=0; i:=0; |
Поки x<=b |
| x:=x+h; si:=0;i:=i+1 |
| Виведення похибки |
Вихід |
| Обчислення за методом Чебишева |
| Виведення результатів |
Для t від 1 до N |
| si:=si+f(x-h/2+h/2*t[k]) |
| Sum:=sum+si; |
 |