Лабораторная работа на тему Интерполяция функций 2
Работа добавлена на сайт bukvasha.net: 2013-11-08Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Министерство образования Российской Федерации.
Хабаровский государственный Технический Университет.
Кафедра «Прикладная математика и информатика»
Лабораторная работа №4
по дисциплине «Вычислительные методы линейной алгебры».
Интерполяция функций.
Вариант 4
Выполнил: ст. гр. ПМ 11 Крамарев Д. В.
Проверил: д.ф.-м.н., проф. Чехонин К.А.
Хабаровск 2004
Хабаровский государственный Технический Университет.
Кафедра «Прикладная математика и информатика»
Лабораторная работа №4
по дисциплине «Вычислительные методы линейной алгебры».
Интерполяция функций.
Вариант 4
Выполнил: ст. гр. ПМ 11 Крамарев Д. В.
Проверил: д.ф.-м.н., проф. Чехонин К.А.
Хабаровск 2004
Задание.
1) Построить интерполяционный многочлен Ньютона. Начертить график и отметить на нем узлы интерполяции. Вычислить значения в точке х=1.25.
2) Построить интерполяционный многочлен Лагранжа. Начертить график и отметить на нем узлы интерполяции. Вычислить значение в точке х=1.2.
3) Выполнить интерполяцию сплайнами третьей степени. Построить график и отметить на нем узлы интерполяции.
Постановка задачи интерполяция.
Пусть известные значения функции образуют следующую таблицу:
При этом требуется получить значение функции f в точке x, принадлежащей
отрезку [x0..xn] но не совпадающей ни с одним значением xi.Часто при этом не известно аналитическое выражение функции f(x), или оно не пригодно для вычислений.
В этих случаях используется прием построения приближающей функции F(x), которая очень близка к f(x) и совпадает с ней в точках x0, x1, x2,... xn. При этом нахождение приближенной функции называется интерполяцией, а точки x0,x1,x2,...xn - узлами интерполяции. Обычно интерполирующую ищут в виде полинома n степени:
Pn(x)=a0xn+a1xn-1+a2xn-2+...+an-1x+an
Для каждого набора точек имеется только один интерполяционный многочлен, степени не больше n. Однозначно определенный многочлен может быть представлен в различных видах. Рассмотрим интерполяционный многочлен Ньютона и Лагранжа.
Интерполяционная формула Лагранжа.
Формула Лагранжа является наиболее общей, может применяться к таким узлам интерполяции, что расстояние между соседними узлами не постоянная величина.
Построим интерполяционный полином Ln(x) степени не больше n, и для которого выполняются условия Ln(xi)=yi . Запишем его в виде суммы:
Ln(x)=l0(x)+ l1(x)+ l2(x)+...+ ln(x), (1)
где lk(xi)= yi, если i=k, и lk(xi)= 0, если i≠k;
Тогда многочлен lk(x) имеет следующий вид:

 lk(x)= (2)
lk(x)= (2)
Подставим (2) в (1) и перепишем Ln(x) в виде:
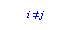

Если функция f(x), подлежащая интерполяции, дифференцируема больше чем n+1 раз, то погрешность интерполяции оценивается следующим образом:
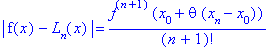
 где0<θ<1 (3)
где0<θ<1 (3)
Интерполяционная формула Ньютона.
Построение интерполяционного многочлена в форме Ньютона применяется главным образом когда разность xi+1-xi=h постоянна для всех значений x=0..n-1.
Конечная разность k-го порядка:
Δyi=yi+1-yi
Δ2yi= Δyi+1- Δyi=yi+2-2yi+1+yi
………………………………
Δkyi=yi+k-kyi+1-k+k(k-1)/2!*yi+k-2+...+(-1)kyi
Будем искать интерполяционный многочлен в виде:
Pn(x)=a0+a1(x-x0)+a2(x-x0)(x-x1)+...+an(x-x0)(x-x1)...(x-xn-1)
Найдем значения коэффициентов a0, a1, a2, ...,an:
Полагая x=x0, находим a0=P(x0)=y0;
Далее подставляя значения x1, x2, ...,xn получаем:
a1=Δy0/h
a2=Δ2y0/2!h2
a3=Δ3y0/3!h3
....................
an=Δny0/n!hn
Таким образом:
Pn(x)=y0+ Δy0/h*(x-x0)+ Δ2y0/2!h2*(x-x0)(x-x1)+...+ Δny0/n!hn*(x-x0)(x-x1)...(x-xn-1) (1)
Практически формула (1) применяется в несколько ином виде:
Возьмем: t=(x-x0)/h, тогда x=x0+th и формула (1) переписывается как:
Pn(x)=y0+tΔy0+t(t-1)/2! Δ2y0+...+t(t-1)...(t-n+1)/n!Δny0 (2)
Формула (2) называется интерполяционной формулой Ньютона.
Погрешность метода Ньютона оценивается следующим образом:
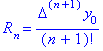
 (3)
(3)
Интерполяция сплайнами.
При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для проведения вычислений.
Высокой степени многочленов можно избежать, разбив отрезок интерполирования на несколько частей, с построением в каждой части своего интерполяционного полинома. Такой метод называется интерполяцией сплайнами. Наиболее распространенным является построение на каждом отрезке [xi, xi+1], i=0..n-1 кубической функции. При этом сплайн – кусочная функция, на каждом отрезке заданная кубической функцией, является кусочно-непрерывной, вместе со своими первой и второй производной.
Будем искать кубический сплайн на каждом из частичных отрезков [xi, xi+1] в виде:
 , где ai,bi,ci,di – неизвестные.
, где ai,bi,ci,di – неизвестные.
Из того что Si(xi)=yi получим:

В силу непрерывности потребуем совпадения значений в узлах, т.е.:
 ,i=0..n-1; (1)
,i=0..n-1; (1)
Также потребуем совпадения значений первой и второй производной:
 ,i=0..n-2; (2)
,i=0..n-2; (2)
 ,i=0..n-2; (3)
,i=0..n-2; (3)
Из (1) получим n линейных уравнений с 3n неизвестными
 ,i=0..n-1; (1*)
,i=0..n-1; (1*)
Из (2) и (3) получим 2(n-1) линейных уравнений с теми же неизвестными:
 ,i=0..n-1; (2*)
,i=0..n-1; (2*)
 ,i=1..n-1; (3*)
,i=1..n-1; (3*)
Недостающие два уравнения определим следующим образом. Предположим, что в точках х0 и хn производная равна нулю и получим еще два уравнения. Получим систему из 3*n линейных уравнений с 3*n неизвестными. Решим ее любым из методов и построим интерполяционную функцию, такую что на отрезке [xi, xi+1] она равна Si.
Метод Лагранжа
procedure TForm1.Button1Click(Sender: TObject);
type tip=array of real;
var x,y:tip;
i,j,n:byte;
p,s,xx:real;
begin
n:=edt.Count;
setlength(x,n);
setlength(y,n);
for i:=0 to n-1 do x[i]:=edt.massiv[i];edt.Lines.Delete(0);
for i:=0 to n-1 do y[i]:=edt.massiv[i];edt.Lines.Delete(0);
xx:=strtofloat(edt.Text);
edt.Lines.Delete(0);
s:=0;
for i:=0 to n-1 do
begin
p:=1;
for j:=0 to n-1 do if i<>j then p:=p*(xx-x[j])/(x[i]-x[j]);
p:=p*y[i];
s:=s+p;
end;
edt.writer('',1);
edt.writer('',s,1);
end;
Сплайн – интерполяция (программа составляет систему линейных уравнений, решая которую находим коэффициенты кубических сплайнов).
procedure TForm1.Button1Click(Sender: TObject);
var b,c,d,x,y:array of real;
urm:array of array of real;
i,j,k,n :byte;
begin
n:=edt.Count;
setlength(x,n);setlength(y,n);
for i:=0 to n-1 do x[i]:=edt.massiv[i];edt.Lines.Delete(0);
for i:=0 to n-1 do y[i]:=edt.massiv[i];edt.Lines.Delete(0);
setlength(b,n-1);setlength(c,n-1);setlength(d,n-1);
setlength(urm,3*(n-1),3*(n-1)+1);
for i:=0 to 3*(n-1)-1 do
for j:=0 to 3*(n-1) do urm[i,j]:=0;
for i:=0 to n-1 do edt.writer(' ',y[i],0);
for i:=0 to n-2 do
begin
urm[i,3*i+0]:=x[i+1]-x[i];
urm[i,3*i+1]:=(x[i+1]-x[i])*(x[i+1]-x[i]);
urm[i,3*i+2]:=(x[i+1]-x[i])*(x[i+1]-x[i])*(x[i+1]-x[i]);
urm[i,3*(n-1)]:=y[i+1]-y[i];
end;
for i:=0 to n-3 do
begin
urm[i+n-1,3*i+0]:=1;
urm[i+n-1,3*i+1]:=2*(x[i+1]-x[i]);
urm[i+n-1,3*i+2]:=3*(x[i+1]-x[i])*(x[i+1]-x[i]);
urm[i+n-1,3*i+3]:=-1;
end;
for i:=0 to n-3 do
begin
urm[i+2*n-3,3*i+1]:=1;
urm[i+2*n-3,3*i+2]:=3*(x[i+1]-x[i]);
urm[i+2*n-3,3*i+4]:=-1;
end;
urm[3*n-5,0]:=1; urm[3*n-5,3*(n-1)]:=0;
urm[3*n-4,3*(n-1)-3]:=1;urm[i+2*n-3,3*(n-1)-2]:=2*(y[n-1]-y[n-2])]
urm[3*n-4,3*(n-1)-1]:=3*(y[n-1]-y[n-2]) *(y[n-1]-y[n-2]);
urm[i+2*n-3,3*(n-1)]:=0
for i:=0 to 3*(n-1)-1 do
begin
edt.writer('',1);
for j:=0 to 3*(n-1) do edt.writer(' ',urm[i,j],0);
end;
end;
Выполнить интерполяцию сплайнами третьей степени. Построить график и отметить на нем узлы интерполяции.
Решение.
Будем искать кубический сплайн на каждом из частичных отрезков [xi, xi+1], i=0..2 в виде:
 , где ai,bi,ci,di – неизвестные.
, где ai,bi,ci,di – неизвестные.
Из того что Si(xi)=yi получим:

В соответствии с теоретическим положениями изложенными выше, составим систему линейных уравнений, матрица которой будет иметь вид:


При этом мы потребовали равенства производной нулю.
Решая систему уравнений получим вектор решений [b1,c1,d1,b2,c2,d2]:

Подставляя в уравнение значения b1,c1,d1, получим на отрезке [7..9]:

Если выражение упростить то:

Аналогично подставляя в уравнение значения b2,c2,d2, получим на отрезке [9..13]:

или 
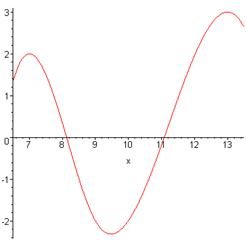
График имеет вид:
Метод Ньютона
procedure TForm1.Button1Click(Sender: TObject);
type tip=array of real;
var x,y:tip;
i,j,n:byte;
p,s,xx,t,h:real;
kp:array of array of real;
begin
n:=edt.Count;
setlength(x,n);
setlength(y,n);
for i:=0 to n-1 do x[i]:=edt.massiv[i];edt.Lines.Delete(0);
for i:=0 to n-1 do y[i]:=edt.massiv[i];edt.Lines.Delete(0);
xx:=strtofloat(edt.Text);
edt.Lines.Delete(0);
setlength(kp,n,n);
for i:=0 to n-1 do for j:=0 to n-1 do kp[i,j]:=0;
for i:=0 to n-1 do kp[0,i]:=y[i];
for i:= 1 to n-1 do
for j:=0 to n-i-1 do
kp[i,j]:=kp[i-1,j+1]-kp[i-1,j];
for i:= 0 to n-1 do
begin
for j:=0 to n-1 do edt.writer(' ',kp[i,j],0);
edt.writer('',1);
end;
edt.writer('',1);
h:=0.5;
t:=(xx-x[0])/h;
s:=y[0];
for i:=1 to n-1 do
begin
p:=1;
for j:=0 to i-1 do p:=p*(t-j)/(j+1);
s:=s+p*kp[i,0];
end;
edt.writer('',s,1);;
end;
Построить интерполяционный многочлен Ньютона. Начертить график и отметить на нем узлы интерполяции. Вычислить значение функции в точке х=1.25.
Решение.
Построим таблицу конечных разностей в виде матрицы:

Воспользуемся интерполяционной формулой Ньютона:
Pn(x)=y0+tΔy0+t(t-1)/2! Δ2y0+...+t(t-1)...(t-n+1)/n!Δny0
Подставив значения получим многочлен пятой степени, упростив который получим:
P5(x)=2.2x5-24x4+101.783x3-20.2x2+211.417x-80.7
Вычислим значение функции в точке x=1.25; P(1.25)=2.0488;
График функции имеет вид:

Построить интерполяционный многочлен Лагранжа. Начертить график и отметить на нем узлы интерполяции. Вычислить значение в точке х=1.2.
Решение.
Построим интерполяционный многочлен Лагранжа L4(x), подставив значения из таблицы в формулу:

Напишем программу и вычислим значение многочлена в точке х=1.2:
L4(1.2)=5.657;
Полученный многочлен имеет четвертую степень. Упростим его и получим:
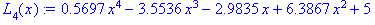
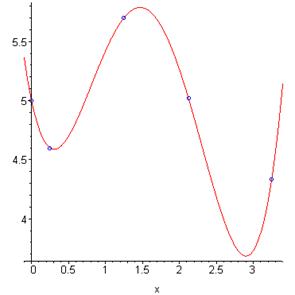
Построим график полученного полинома:
1) Построить интерполяционный многочлен Ньютона. Начертить график и отметить на нем узлы интерполяции. Вычислить значения в точке х=1.25.
| xi | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
| yi | 0.5 | 2.2 | 2 | 1.8 | 0.5 | 2.25 |
| xi | 0 | 0.25 | 1.25 | 2.125 | 3.25 |
| yi | 5.0 | 4.6 | 5.7 | 5.017 | 4.333 |
| xi | 7 | 9 | 13 |
| yi | 2 | -2 | 3 |
Постановка задачи интерполяция.
Пусть известные значения функции образуют следующую таблицу:
| x0 | x1 | x2 | ... | Xn-1 | xn |
| y0 | y1 | y2 | ... | yn-1 | yn |
отрезку [x0..xn] но не совпадающей ни с одним значением xi.Часто при этом не известно аналитическое выражение функции f(x), или оно не пригодно для вычислений.
В этих случаях используется прием построения приближающей функции F(x), которая очень близка к f(x) и совпадает с ней в точках x0, x1, x2,... xn. При этом нахождение приближенной функции называется интерполяцией, а точки x0,x1,x2,...xn - узлами интерполяции. Обычно интерполирующую ищут в виде полинома n степени:
Pn(x)=a0xn+a1xn-1+a2xn-2+...+an-1x+an
Для каждого набора точек имеется только один интерполяционный многочлен, степени не больше n. Однозначно определенный многочлен может быть представлен в различных видах. Рассмотрим интерполяционный многочлен Ньютона и Лагранжа.
Интерполяционная формула Лагранжа.
Формула Лагранжа является наиболее общей, может применяться к таким узлам интерполяции, что расстояние между соседними узлами не постоянная величина.
Построим интерполяционный полином Ln(x) степени не больше n, и для которого выполняются условия Ln(xi)=yi . Запишем его в виде суммы:
Ln(x)=l0(x)+ l1(x)+ l2(x)+...+ ln(x), (1)
где lk(xi)= yi, если i=k, и lk(xi)= 0, если i≠k;
Тогда многочлен lk(x) имеет следующий вид:
| (x-x0) (x-x1)...(x-xi-1) (x-xi+1) (x-xn) (xi-x0)(xi-x1)...(xi-xi-1)(xi-xi+1)(xi-xn) |
 lk(x)= (2)
lk(x)= (2) Подставим (2) в (1) и перепишем Ln(x) в виде:
| i ≠ j |
Если функция f(x), подлежащая интерполяции, дифференцируема больше чем n+1 раз, то погрешность интерполяции оценивается следующим образом:
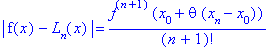
Интерполяционная формула Ньютона.
Построение интерполяционного многочлена в форме Ньютона применяется главным образом когда разность xi+1-xi=h постоянна для всех значений x=0..n-1.
Конечная разность k-го порядка:
Δyi=yi+1-yi
Δ2yi= Δyi+1- Δyi=yi+2-2yi+1+yi
………………………………
Δkyi=yi+k-kyi+1-k+k(k-1)/2!*yi+k-2+...+(-1)kyi
Будем искать интерполяционный многочлен в виде:
Pn(x)=a0+a1(x-x0)+a2(x-x0)(x-x1)+...+an(x-x0)(x-x1)...(x-xn-1)
Найдем значения коэффициентов a0, a1, a2, ...,an:
Полагая x=x0, находим a0=P(x0)=y0;
Далее подставляя значения x1, x2, ...,xn получаем:
a1=Δy0/h
a2=Δ2y0/2!h2
a3=Δ3y0/3!h3
....................
an=Δny0/n!hn
Таким образом:
Pn(x)=y0+ Δy0/h*(x-x0)+ Δ2y0/2!h2*(x-x0)(x-x1)+...+ Δny0/n!hn*(x-x0)(x-x1)...(x-xn-1) (1)
Практически формула (1) применяется в несколько ином виде:
Возьмем: t=(x-x0)/h, тогда x=x0+th и формула (1) переписывается как:
Pn(x)=y0+tΔy0+t(t-1)/2! Δ2y0+...+t(t-1)...(t-n+1)/n!Δny0 (2)
Формула (2) называется интерполяционной формулой Ньютона.
Погрешность метода Ньютона оценивается следующим образом:
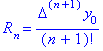
Интерполяция сплайнами.
При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для проведения вычислений.
Высокой степени многочленов можно избежать, разбив отрезок интерполирования на несколько частей, с построением в каждой части своего интерполяционного полинома. Такой метод называется интерполяцией сплайнами. Наиболее распространенным является построение на каждом отрезке [xi, xi+1], i=0..n-1 кубической функции. При этом сплайн – кусочная функция, на каждом отрезке заданная кубической функцией, является кусочно-непрерывной, вместе со своими первой и второй производной.
Будем искать кубический сплайн на каждом из частичных отрезков [xi, xi+1] в виде:
Из того что Si(xi)=yi получим:
В силу непрерывности потребуем совпадения значений в узлах, т.е.:
Также потребуем совпадения значений первой и второй производной:
Из (1) получим n линейных уравнений с 3n неизвестными
Из (2) и (3) получим 2(n-1) линейных уравнений с теми же неизвестными:
Недостающие два уравнения определим следующим образом. Предположим, что в точках х0 и хn производная равна нулю и получим еще два уравнения. Получим систему из 3*n линейных уравнений с 3*n неизвестными. Решим ее любым из методов и построим интерполяционную функцию, такую что на отрезке [xi, xi+1] она равна Si.
Метод Лагранжа
procedure TForm1.Button1Click(Sender: TObject);
type tip=array of real;
var x,y:tip;
i,j,n:byte;
p,s,xx:real;
begin
n:=edt.Count;
setlength(x,n);
setlength(y,n);
for i:=0 to n-1 do x[i]:=edt.massiv[i];edt.Lines.Delete(0);
for i:=0 to n-1 do y[i]:=edt.massiv[i];edt.Lines.Delete(0);
xx:=strtofloat(edt.Text);
edt.Lines.Delete(0);
s:=0;
for i:=0 to n-1 do
begin
p:=1;
for j:=0 to n-1 do if i<>j then p:=p*(xx-x[j])/(x[i]-x[j]);
p:=p*y[i];
s:=s+p;
end;
edt.writer('',1);
edt.writer('',s,1);
end;
Сплайн – интерполяция (программа составляет систему линейных уравнений, решая которую находим коэффициенты кубических сплайнов).
procedure TForm1.Button1Click(Sender: TObject);
var b,c,d,x,y:array of real;
urm:array of array of real;
i,j,k,n :byte;
begin
n:=edt.Count;
setlength(x,n);setlength(y,n);
for i:=0 to n-1 do x[i]:=edt.massiv[i];edt.Lines.Delete(0);
for i:=0 to n-1 do y[i]:=edt.massiv[i];edt.Lines.Delete(0);
setlength(b,n-1);setlength(c,n-1);setlength(d,n-1);
setlength(urm,3*(n-1),3*(n-1)+1);
for i:=0 to 3*(n-1)-1 do
for j:=0 to 3*(n-1) do urm[i,j]:=0;
for i:=0 to n-1 do edt.writer(' ',y[i],0);
for i:=0 to n-2 do
begin
urm[i,3*i+0]:=x[i+1]-x[i];
urm[i,3*i+1]:=(x[i+1]-x[i])*(x[i+1]-x[i]);
urm[i,3*i+2]:=(x[i+1]-x[i])*(x[i+1]-x[i])*(x[i+1]-x[i]);
urm[i,3*(n-1)]:=y[i+1]-y[i];
end;
for i:=0 to n-3 do
begin
urm[i+n-1,3*i+0]:=1;
urm[i+n-1,3*i+1]:=2*(x[i+1]-x[i]);
urm[i+n-1,3*i+2]:=3*(x[i+1]-x[i])*(x[i+1]-x[i]);
urm[i+n-1,3*i+3]:=-1;
end;
for i:=0 to n-3 do
begin
urm[i+2*n-3,3*i+1]:=1;
urm[i+2*n-3,3*i+2]:=3*(x[i+1]-x[i]);
urm[i+2*n-3,3*i+4]:=-1;
end;
urm[3*n-5,0]:=1; urm[3*n-5,3*(n-1)]:=0;
urm[3*n-4,3*(n-1)-3]:=1;urm[i+2*n-3,3*(n-1)-2]:=2*(y[n-1]-y[n-2])]
urm[3*n-4,3*(n-1)-1]:=3*(y[n-1]-y[n-2]) *(y[n-1]-y[n-2]);
urm[i+2*n-3,3*(n-1)]:=0
for i:=0 to 3*(n-1)-1 do
begin
edt.writer('',1);
for j:=0 to 3*(n-1) do edt.writer(' ',urm[i,j],0);
end;
end;
Выполнить интерполяцию сплайнами третьей степени. Построить график и отметить на нем узлы интерполяции.
| xi | 7 | 9 | 13 |
| yi | 2 | -2 | 3 |
Будем искать кубический сплайн на каждом из частичных отрезков [xi, xi+1], i=0..2 в виде:
Из того что Si(xi)=yi получим:
В соответствии с теоретическим положениями изложенными выше, составим систему линейных уравнений, матрица которой будет иметь вид:

При этом мы потребовали равенства производной нулю.
Решая систему уравнений получим вектор решений [b1,c1,d1,b2,c2,d2]:
Подставляя в уравнение значения b1,c1,d1, получим на отрезке [7..9]:
Если выражение упростить то:
Аналогично подставляя в уравнение значения b2,c2,d2, получим на отрезке [9..13]:
или
График имеет вид:

Метод Ньютона
procedure TForm1.Button1Click(Sender: TObject);
type tip=array of real;
var x,y:tip;
i,j,n:byte;
p,s,xx,t,h:real;
kp:array of array of real;
begin
n:=edt.Count;
setlength(x,n);
setlength(y,n);
for i:=0 to n-1 do x[i]:=edt.massiv[i];edt.Lines.Delete(0);
for i:=0 to n-1 do y[i]:=edt.massiv[i];edt.Lines.Delete(0);
xx:=strtofloat(edt.Text);
edt.Lines.Delete(0);
setlength(kp,n,n);
for i:=0 to n-1 do for j:=0 to n-1 do kp[i,j]:=0;
for i:=0 to n-1 do kp[0,i]:=y[i];
for i:= 1 to n-1 do
for j:=0 to n-i-1 do
kp[i,j]:=kp[i-1,j+1]-kp[i-1,j];
for i:= 0 to n-1 do
begin
for j:=0 to n-1 do edt.writer(' ',kp[i,j],0);
edt.writer('',1);
end;
edt.writer('',1);
h:=0.5;
t:=(xx-x[0])/h;
s:=y[0];
for i:=1 to n-1 do
begin
p:=1;
for j:=0 to i-1 do p:=p*(t-j)/(j+1);
s:=s+p*kp[i,0];
end;
edt.writer('',s,1);;
end;
Построить интерполяционный многочлен Ньютона. Начертить график и отметить на нем узлы интерполяции. Вычислить значение функции в точке х=1.25.
| xi | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
| yi | 0.5 | 2.2 | 2 | 1.8 | 0.5 | 2.25 |
Построим таблицу конечных разностей в виде матрицы:

Воспользуемся интерполяционной формулой Ньютона:
Pn(x)=y0+tΔy0+t(t-1)/2! Δ2y0+...+t(t-1)...(t-n+1)/n!Δny0
Подставив значения получим многочлен пятой степени, упростив который получим:
P5(x)=2.2x5-24x4+101.783x3-20.2x2+211.417x-80.7
Вычислим значение функции в точке x=1.25; P(1.25)=2.0488;
График функции имеет вид:

Построить интерполяционный многочлен Лагранжа. Начертить график и отметить на нем узлы интерполяции. Вычислить значение в точке х=1.2.
| xi | 0 | 0.25 | 1.25 | 2.125 | 3.25 |
| yi | 5.0 | 4.6 | 5.7 | 5.017 | 4.333 |
Построим интерполяционный многочлен Лагранжа L4(x), подставив значения из таблицы в формулу:
Напишем программу и вычислим значение многочлена в точке х=1.2:
L4(1.2)=5.657;
Полученный многочлен имеет четвертую степень. Упростим его и получим:
Построим график полученного полинома:
