Реферат на тему Математическое моделирование естествознания
Работа добавлена на сайт bukvasha.net: 2015-06-25Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Нижегородский Государственный университет
им. Н. И. Лобачевского Реферат на тему Математическое моделирование естествознания выполнил: ст. Шишкин Тимофей 731 группа проверил: Антаков Р.А. Нижний Новгород 1999г. Структура естественнонаучных знаний Естественные и гуманитарные науки. Наука занимается изучением объективно существующих ( т.е. существующих независимо от чьего-либо сознания) объектов и явлений природы. Вопрос о том, существует ли окружающий нас мир сам по себе или он является продуктом деятельности разума (принадлежащего некому высшему существу или каждому конкретному индивиду) составляет суть т.н. основного вопроса философии, классически формулируемом в виде дилеммы о первичности материи или сознания. В зависимости от ответа на основной вопрос философы подразделяются на материалистов (признают объективное существование окружающего нас мира, возникшего в результате саморазвития материи), объективных идеалистов (признают объективное существование мира, возникшего как результат деятельности высшего разума) и субъективных идеалистов (считают, что окружающий нас мир не существует реально, а есть плод воображения отдельного индивида) . По-видимому невозможно дать экспериментально обоснованного ответа на основной вопрос философии, хотя большинство естествоиспытателей являются приверженцами материалистических концепций. Все существующие научные дисциплины условно (любая классификация носит приближенный характер и неполно отражает истинную суть вещей!) разделены на две основные группы: естественнонаучные (занимаются изучением объектов природы и явлений, не являющихся продуктом деятельности человека или человечества) и гуманитарные (изучают явления объекты, возникшие как результат деятельности человека). Предмет естествознания - факты и явления, которые воспринимаются нашими органами чувств. Задача ученого- обобщить эти факты и создать теоретическую модель, включающую законы, управляющие явлениями природы. Следует различать факты опыта, эмпирические обобщения и теории, которые формулируют законы науки. Явления, например, тяготение, непосредственно даны в опыте; законы науки, например, закон всемирного тяготения - варианты объяснения явлений. Факты науки, будучи установленными, сохраняют свое постоянное значение; законы могут быть изменены в ходе развития науки, как, скажем, закон всемирного тяготения был скорректирован после создания теории относительности. Значение чувств и разума в процессе нахождения истины - сложный философский вопрос. В науке признается истиной то положение, которое подтверждается воспроизводимым опытом. Основной принцип естествознания гласит: знания о природе должны допускать эмпирическую проверку. Не в том смысле, что каждое частное утверждение должно обязательно эмпирически проверяться, а в том, что опыт, в конечном счете, является решающим аргументом принятия данной теории. Естествознание в полном смысле слова общезначимо и дает “родовую” истину, т.е. истину, пригодную и принимаемую всеми людьми. Поэтому оно традиционно рассматривалось в качестве эталона научной объективности. Другой крупный комплекс наук - обществознание - напротив, всегда был связан с групповыми ценностями и интересами, имеющимися как у самого ученого, так и в предмете исследования. Поэтому в методологии обществоведения наряду с объективными методами исследования приобретает большое значение переживание изучаемого события, субъективное отношение к нему и т.п. От технических наук естествознание отличается нацеленностью на познание, а не на помощь в преобразовании мира, а от математики тем, что исследует природные, а не знаковые системы. Следует учитывать различие между естественными и техническими науками, с одной стороны, и фундаментальными и прикладными - с другой. Фундаментальные науки - физика, химия, астрономия - изучают базисные структуры мира, а прикладные - занимаются применением результатов фундаментальных исследований для решения как познавательных, так и социально-практических задач. В этом смысле все технические науки являются прикладными, но далеко не все прикладные науки относятся к техническим. Такие науки, как физика металлов, физика полупроводников являются теоретическими прикладными дисциплинами, а металловедение, полупроводниковая технология - практическими прикладными науками. Однако провести четкую грань между естественными, общественными и техническими науками в принципе нельзя, поскольку имеется целый ряд дисциплин, занимающих промежуточное положение или являющихся комплексными по своей сути. Так, на стыке естественных и общественных наук находится экономическая география, на стыке естественных и технических - бионика, а комплексной междисциплинарной дисциплиной, которая включает и естественные, и общественные, и технические разделы, является социальная экология. Уровни организации материи и иерархия естественно научных знаний. Окружающие нас объекты природы имеют внутреннюю структуру, т.е. в свою очередь сами состоят из других объектов (яблоко состоит из клеток растительной ткани, которая сложена из молекул, являющихся объединениями атомов и т.д.). При этом естественным образом возникают различные по сложности уровни организации материи: космический, планетарный, геологический, биологический, химический, физический. Представители естественных наук, занимающиеся изучением объектов какого-либо уровня могут достичь их полного описания лишь основываясь на знаниях более “низкого” (элементарного) уровня (невозможно понять законы жизнедеятельности клетки, не изучив химизм протекающих в ней реакций). Однако реальные возможности каждого отдельного исследователя весьма ограничены (человеческой жизни недостаточно не только для того, чтобы плодотворно заниматься изучением сразу нескольких уровней, но даже заведомо не хватает на сколько-нибудь полное освоение уже накопленных знаний о каком-то одном). Из-за этого возникло деление естественно научных знаний на отдельные дисциплины, примерно соответствующие вышеперечисленным уровням организации материи: астрономию, экологию, геологию, биологию, химию и физику. Специалисты, работающие на своем уровне, опираются на знания смежных наук, находящихся ниже по иерархической лестнице. Исключение составляет физика, находящаяся на “самом нижнем этаже” человеческих знаний (“составляющая их фундамент”): исторически сложилось так, что в ходе развития этой науки обнаруживались все более “элементарные” уровни организации материи (молекулярный, атомный, элементарных частиц...), изучением которых по-прежнему занимались физики. Естественные науки различных уровней не обособлены друг от друга. При изучении высокоорганизованных систем возникает естественная потребность в информации о составляющих их элементах, предоставляемой дисциплинами “более низких” уровней. При изучении же “элементарных” объектов весьма полезны знания о их поведении в сложных системах, где при взаимодействиях с другими элементами проявляются свойства изучаемых. Примером взаимодействия наук разных уровней может служить разработка Ньютоном классической теории тяготения (физический уровень), возникшей на основе законов движения планет Кеплера (астрономический уровень), и современные концепции эволюции Вселенной, немыслимые без учета законов гравитации. Естественные науки, находящиеся на нижних этажах иерархической лестницы, несомненно проще вышестоящих, поскольку занимаются более простыми объектами (строение электронного облака атома углерода, несомненно “проще пареной репы”, содержащей множество атомов с такими облаками!). Однако, именно из-за простоты изучаемых объектов науки нижних уровней сумели накопить гораздо больше фактической информации и создать более законченные теории. Место математики среди естественных наук. Обсуждавшаяся выше структура естествознания не содержит математики, без которой невозможна ни одна из современных точных наук. Это связано с тем, что сама математика не является естественной наукой в полном смысле этого понятия, поскольку не занимается изучением каких-либо объектов или явлений реального мира. В основе математики лежат аксиомы, придуманные человеком. Для математика не имеет решающего значения вопрос, выполняются ли эти аксиомы в реальности или нет (напр. в настоящее время благополучно сосуществует несколько геометрий, основанных на несовместных друг с другом системах аксиом). Если математика заботит лишь логическая строгость его выводов, делаемых на основе аксиом и предшествующих теорем, естествоиспытателю важно, соответствует ли его теоретическое построение реальности. При этом в качестве критерия истинности естественнонаучных знаний выступает эксперимент, в ходе которого осуществляется проверка теоретических выводов. В ходе изучения свойств реальных объектов часто оказывается так, что они приближенно соответствуют аксиоматике того или иного раздела математики (напр. положение небольшого тела можно приближенно описать, задав три его координаты, совокупность которых можно рассматривать как вектор в трехмерном пространстве). При этом ранее доказанные в математике утверждения (теоремы) оказываются применимыми к таким объектам. Кроме сказанного, математика играет роль очень лаконичного, экономного и емкого языка, термины которого применимы к внешне совершенно разнородным объектам окружающего мира (вектором можно назвать и совокупность координат точки, и характеристику силового поля, и компонентный состав химической смести, и характеристику экономико-географического положения местности). Очевидно, что более простые объекты нашего мира удовлетворяют более простым системам аксиом, следствия из которых математиками изучены более полно. Поэтому естественные науки “низших” уровней оказываются более математизированными. Опыт развития современного естествознания показывает, что на определенном этапе развития естественно научных дисциплин неизбежно происходит их математизация, результатом которой является создание логически стройных формализованных теорий и дальнейшее ускоренное развитие дисциплины. Приближенный характер естественнонаучных знаний. Несмотря на то, что естественные науки часто называют точными, практически любое конкретное утверждение в них носит приближенный характер. Причиной этого является не только несовершенство измерительных приборов, но и ряд принципиальных ограничений на точность измерений, установленных современной физикой. Кроме того, практически все реально наблюдаемые явления столь сложны и содержат такое множество процессов между взаимодействующими объектами, что их исчерпывающее описание оказывается не только технически невозможным, но и практически бессмысленным (человеческое сознание способно воспринять лишь весьма ограниченный объем информации). На практике исследуемая система сознательно упрощается путем ее замены моделью, учитывающей только самые важные элементы и процессы. По мере развития теории модели усложняются, постепенно приближаясь к реальности. Основные этапы развития естествознания могут быть выделены, исходя из различных соображений. По мнению автора, в качестве основного критерия следует рассматривать доминирующий среди естествоиспытателей подход к построению их теорий. При этом оказывается возможным выделение трех основных этапов. Естествознание древнего мира. Завершенного деления на дисциплины не существовало, создаваемые концепции в своем большинстве носили мировоззренческий характер. Экспериментальный метод познания в принципе допускался, но роль решающего критерия истинности эксперименту не отводилась. Верные наблюдения и гениальные обобщающие догадки сосуществовали с умозрительными и часто ошибочными построениями. Классический период развития естествознания берет свое начало с экспериментальных работ Галилея (18 век) и длится до начала нашего столетия. Характеризуется четким разделением наук на традиционные области и даже несколько гипертрофированной ролью эксперимента в их развитии (“понять- значит измерить”). Эксперимент рассматривается не только как критерий истинности, но и как основной инструмент познания. Вера в истинность экспериментально добытых результатов столь велика, что их начинают распространять на новые области и проблемы, где соответствующей проверки не производилось. При обнаружении расхождений так создаваемых концепций с реально наблюдаемыми явлениями неизбежно возникало недоумение, граничащее с попытками отрицания самой возможности познания окружающего мира. Современное естествознание характеризуется лавинообразным накоплением нового фактического материала и возникновением множества новых дисциплин на стыках традиционных. Резкое удорожание науки, особенно экспериментальной. Как следствие - возрастание роли теоретических исследований, направляющих работу экспериментаторов в области, где обнаружение новых явлений более вероятно. формулировка новых эвристических требований к создаваемым теориям: красоты, простоты, внутренней непротиворечивости, экспериментальной проверяемости, соответствия (преемственности). Роль эксперимента, как критерия истинности знания, сохраняется, но признается , что само понятие истинности не имеет абсолютного характера: утверждения, истинные при определенных условиях, при выходе за границы, в рамках которых проводилась экспериментальная проверка, могут оказаться приближенными и даже ложными. Современное естествознание утратило присущую классическим знаниям простоту и наглядность. Это произошло главным образом из-за того, что интересы современных исследователей из традиционных для классической науки областей переместились туда, где обычный “житейский” опыт и знания об объектах и происходящих с ними явлениях в большинстве случаев отсутствуют. После триумфа классической механики Ньютона химия в лице Лавуазье, положившего начало систематическому применению весов, встала на количественный путь, а вслед за ней и другие естественные науки. “Таково первое основание, по которому физик не может обойтись без математики; она дает ему единственный язык, на котором он в состоянии изъясняться (А.Пуанкаре.Цит.соч. - С.220)”. Дифференциальное и интегральное исчисление хорошо подходит для описания изменения скоростей движений, а вероятностные методы - для необратимости и создания нового. Все можно описать количественно, и тем не менее, остается проблемой отношение математики к реальности. По мнению одних методологов, чистая математика и логика используют доказательства, но не дают нам никакой информации о мире ( почему Пуанкаре считал, что законы природы конвенциональны), а только разрабатывают средства его описания. Однако, еще Аристотель писал, что число есть промежуточное между частным предметом и идеей, а Галилей полагал, что Книга Природы написана языком математики. Не имея непосредственного отношения к реальности, математика не только описывает эту реальность, но и позволяет, как в уравнениях Максвелла, делать новые интересные и неожиданные выводы о реальности из теории, которая представлена в математической форме. Как же объяснить непостижимую истинность математики и ее пригодность для естествознания? Может все дело в том, что “ механизм математического творчества, например, не отличается существенно от механизма какого бы то ни было иного творчества”( А.Пуанкаре.Цит.соч.-С.285)? Или более пригодны более сложные, системные объяснения? По мнению некоторых методологов, законы природы не сводятся к написанным на бумаге математическим соотношениям. Их надо понимать как любой вид организованности идеальных прообразов вещей, или пси-функций. Есть три вида организованности: простейший - числовые соотношения; более сложный - ритмика 1-го порядка, изучаемая математической теорией групп; самый сложный - ритмика 2-го порядка - “слово”. Два первых вида организованности наполняют Вселенную мерой и гармонией, третий - смыслом. В рамках этого объяснения математика занимает свое особое место в познании. Работа над любой математической моделью начинается со сбора и анализа фактического материала. Определяются цели моделирования. Выделяются главные черты изучаемого объекта или явления. Вводятся формализованные характеристики. Принимаются правила работы с ними. В результате возникает математический объект, который и называется математической моделью. Разрабатываются методы математического анализа модели, которыми она исследуется. Полученные результаты математического моделирования интерпретируются в рамках исходного фактического материала, что позволяет оценить степень адекватности модели. Результаты моделирования не должны противоречить выделенным ранее ключевым экспериментальным фактам. Одновременно, модель не может объяснить все стороны изучаемого объекта или явления. Хорошая модель, кроме объяснения известных, должна давать возможность предсказывать новые свойства. Математическое моделирование широко используется там, где экспериментальные исследования трудоемки и дорогостоящи, или вообще невозможны (например, в изучении социальных явлений). Кроме задачи о прогнозе, математическое моделирование помогает классифицировать и систематизировать фактический материал, увидеть существующие связи в мозаике фактов. Это вытекает из того, что модель является специфическим -ярким и выразительным языком, предназначенным для описания для описания изучаемого объекта или явления. Мир математических моделей разнообразен. Существуют различные схемы их классификации. Однако, каждая модель конкретна и предназначена для описания достаточно узкого круга объектов и явлений. Модели сильно отличаются друг от друга не только предметными областями, но математической терминологией, а также математическими методами их исследования. Предпочтение отдается более простым моделям. Отметим, что “простота” (иногда в ущерб точности)-один из принципов, о котором всегда нужно помнить при разработке математической модели. Математические модели нейронных систем Изучение нейронных систем - одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая совершенная интеллектуальная система - человеческий мозг. Никакой компьютер в настоящее время не может воспроизвести ее феномен. Более того, даже поведение таких относительно простых организмов, как кальмары, в настоящее время в полной мере невозможно смоделировать на компьютере. Законы функционирования отдельных элементов нервной системы в целом не плохо изучены. Однако, законы функционирования ассоциаций нельзя свести законам поведения отдельных элементов. На самом деле об эффектах, обусловленных коллективным поведением нейронных популяций, известно мало. Понятны некоторые самые общие принципы. Например, нейронные системы способны адаптироваться к меняющимся условиям, т.е. им не нужны жесткие программы. Одновременно, последние, хотя бы в форме рефлексов, присутствуют в нервной системе. Экспериментальное изучение эффектов коллективного поведения нейронных систем затруднено. Эти системы слишком сложно устроены. Так в мозге человека и животных каждый нейрон находится под воздействием тысяч других нейронов и, соответственно, влияет на тысячи нейронов. Всего же по современным оценкам в мозге порядка миллиарда нейронов. Огромное значение имеет математическое моделирование, как метод косвенного исследования. Оно помогает понять, какие процессы могут происходить в нейронных популяциях. Затем уже можно пытаться обнаружить соответствующие явления экспериментально. Модели различаются в зависимости от целей моделирования. Некоторые модели достаточно адекватно в деталях описывают поведение отдельных нейронов и помогают понять закономерности их функционирования. Они же являются базовыми для моделей малых нейронных популяций. Для описания больших популяций используют упрощенные модели нейронов. Упор делается на изучение эффектов коллективного поведения. Результаты моделирования используются как в нейрофизиологии, так и в технике. Уже сейчас выпускаются нейронные платы. Пока их возможности невелики. Они используются, например, в обработке изображений, а также при решении некоторых экономических задач. Следует отметить, что сейчас все задачи, которые можно решить с помощью нейронных плат, в принципе можно решить и с помощью обычного компьютера. Однако, нейронные платы увеличивают быстродействие. Перспективным считается направление, связанное с использованием нейронной техники для проведения вычислений. Ряд вычислений на нейроподобных системах может проводиться нетрадиционным способом -путем имитации явлений. Возбудимые системы Нервная клетка, или нейрон является структурной единицей нервной системы живых организмов. Индивидуальные границы нейрона, как и любой другой клетки, определяются клеточной мембраной. В любой клетке существует разность потенциалов между содержимым клетки -цитоплазмой и внеклеточной средой. Мембрана поляризована. Ее внутренняя поверхность заряжена отрицательно по отношению к внешней. Разность потенциалов называют мембранным потенциалом. Его величина составляет несколько десятков милливольт. Причина возникновения мембранного потенциала -неравенство концентраций ионов в цитоплазме и в тканевой жидкости. Это обусловлено тем, что клеточные мембраны обладают избирательной проницаемостью для различных ионов. Живые организмы, все клетки и, в частности, нейроны обладают раздражимостью -способностью реагировать на различного рода воздействия. Реакции носят сложный, комплексный характер, но всегда сопровождаются изменением электрического заряда мембраны. Воздействия, вызывающие реакции, называются раздражителями, или стимулами. Хотя живые организмы состоят из клеток, реакции организма в целом не сводятся к реакциям отдельных клеток. Напомним универсальное правило: закономерности системы не могут быть сведены к закономерностям отдельных элементов. Нервные клетки и некоторые ткани (мышечная, железистая) специально приспособлены к осуществлению быстрых реакций на раздражение. Такие клетки и ткани называются возбудимыми, а их реакция -возбудимостью. Клетки при возбуждении переходят из состояния физиологического покоя в состояние активности. В частности, нервная клетка генерирует один, или несколько электрических импульсов. Это связано с тем, что при возбуждении проницаемость мембраны для ионов резко увеличивается. Возникают ионные токи, что естественно приводит к изменению разности потенциалов на поверхности мембраны. Это изменение мембранного потенциала называется потенциалом действия. Генерируемые нервными клетками импульсы также называются спайками. Группы, тесно следующих друг за другом спайков, называются пачками или берстами. Амплитуды спайков относительно стабильны для каждого типа нейронов, поэтому часто говорят, что нейрон реагирует на раздражение по закону “все, или ничего”. Нервное возбуждение - распространяющийся процесс. Возникнув в одном, или нескольких нейронах, оно передается другим клеткам. Проведение возбуждения обусловлено тем, что потенциал действия, возникнув в одной клетке, становится раздражителем для связанных с ней клеток. То же самое относится к другим возбудимым тканям, например, к сердечной мышце. Согласно наиболее распространенной в настоящее время точки зрения считается, что “сообщения” в нервной системе передаются в виде импульсов “все, или ничего” в форме частотного кода. Обсудим природу мембранного потенциала. Мембрана, отделяющая цитоплазму нейрона от межклеточной среды, состоит в основном из липидов -жироподобных веществ. В нее встроены белковые молекулы. Некоторые молекулы пронизывают липидный слой насквозь, а другие погружены лишь до сердцевины (своеобразные ворсинки). Некоторые белки выполняют роль каналов, осуществляющих транспорт ионов через мембрану. Другие -служат рецепторами, позволяющими нейрону реагировать на поступающие от других нейронов потенциалы действия. Механизмы переноса ионов через мембрану делятся на два класса: пассивный и активный транспорт. Пассивный транспорт не требует затрат энергии. Он определяется двумя факторами. Диффузия способствует выравниванию концентрации растворов. Носители зарядов -ионы перемещаются под действием электрического поля. При активном транспорте за счет химической энергии, освобождающейся при окислении аминокислот, может осуществляться перенос ионов как в области с более высокой их концентрацией, так и против электрических сил. Закономерности пассивного транспорта опираются на некоторые положения электрохимии. Как уже говорилось, мембраны биологического происхождения обладают избирательной проницаемостью. Одни ионы достаточно легко диффундируют через них. Для других ионов мембраны практически непроницаемы. Рассмотрим на примере положение об электрохимическом равновесии. Пусть в сосуд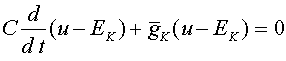 . Отсюда получаем:
. Отсюда получаем: 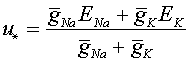 . Одна из первых гипотез о природе мембранного потенциала была высказана в 1902 г. Бернштейном, который использовал положения электрохимии. Он предположил, что предположил, что концентрация ионов
. Одна из первых гипотез о природе мембранного потенциала была высказана в 1902 г. Бернштейном, который использовал положения электрохимии. Он предположил, что предположил, что концентрация ионов 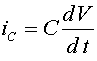 ,
, 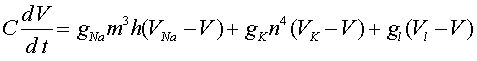 , (6)
, (6) 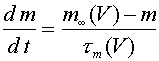 , (7)
, (7) 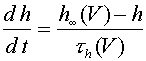 , (8)
, (8) 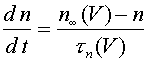 , (9) где, напомним,
, (9) где, напомним, 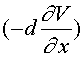 , где направление выбрано в сторону возрастания
, где направление выбрано в сторону возрастания 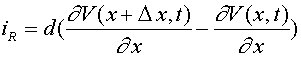 . Используя формулу Лагранжа получим:
. Используя формулу Лагранжа получим: 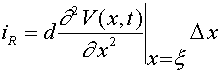 , где
, где 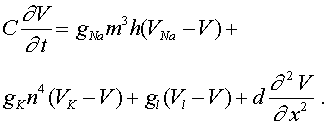 (10) Его часто называют уравнением аксона Ходжкина -Хаксли. В (10) функции
(10) Его часто называют уравнением аксона Ходжкина -Хаксли. В (10) функции 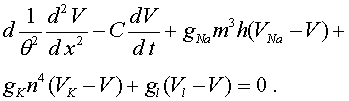 (11) Система (7) -(9), (11) исследовалась численно. Методом подбора было найдено значение скорости
(11) Система (7) -(9), (11) исследовалась численно. Методом подбора было найдено значение скорости 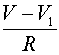 и
и 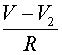 , где
, где 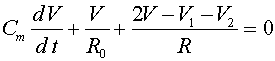 . Для описания мембранных потенциалов
. Для описания мембранных потенциалов 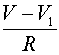 , а для правого -слагаемое
, а для правого -слагаемое 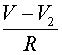 . Это токи, проходящие между соответствующими перехватами и миелинизированным участком. В результате получим уравнения:
. Это токи, проходящие между соответствующими перехватами и миелинизированным участком. В результате получим уравнения: 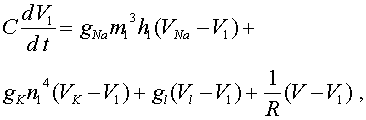
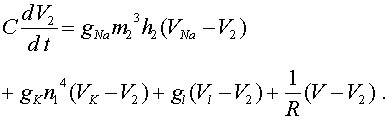 Величины
Величины Как сердцу высказать себя?
Другому как понять тебя?
Поймет ли он, чем ты живешь?
Мысль изреченная есть ложь.
Взрывая, возмутишь ключи,
Питайся ими—и молчи.
Всегда остающийся в предметах исследования науки неразлагаемый рационалистически остаток, т. е. иррациональный остаток, к которому приводят все основные научные эмпирические понятия при логическом анализе, означает, что мы должны принимать во внимание наряду с безусловно необходимыми - достоверными - фактами, характерными для вполне детерминистической классической механики, и факты вероятностные, лежащие в основе надлежащей квантовой механики (с ее соответствующей вероятностной интерпретацией и с характерным для нее принципом неопределенности), а также факты веры, с которыми имеют дело не только все религии, но и атеизм, поскольку “основанные на философских заключениях” “атеистические представления,—как справедливо заметил Вернадский, - по существу тоже предмет веры”. Чуть ли не все подвергая сомнению, Вернадский замечает: “Но это не касается эмпирических обобщений, которые в основе своей существенно отличны от научных теорий и научных гипотез, с которыми они обычно смешиваются”. При этом он считал принципиально необходимым и возможным стремиться к предельно полному охвату природных явлений и самой Природы в целом. Однако в пределе, охватывая в целом Природу, Вселенную, материю (со всеми присущими ей атрибутами, вплоть до Жизни и Разума, в том числе Высшего Разума - с бесконечными потенциальными возможностями), мы по крайней мере в принципе можем и должны получить - и действительно получаем! - не только искомое воистину универсальное (предельно полное) ключевое научное эмпирическое обобщение в виде вполне детерминированных взаимосвязанных периодических систем всевозможных (так называемых эталонных и производных) фундаментальных структурных элементов материи на всех четырех возможных последовательных основных уровнях ее естественной самоорганизации - физическом, химическом, биологическом и психологическом (т. е. на самом деле величайшее атомистическое научное эмпирическое обобщение менделеевского типа), но и адекватное ему столь же универсальное ключевое научное теоретическое обобщение в виде совершенно однотипных по своей симметрии и, соответственно, непосредственно однозначно дедуктивно определяемых по надлежащей математической индукции вполне детерминированных взаимосвязанных периодических систем всевозможных равномерно квантованных собственных значений всех возможных универсальных характеристик рассматриваемых элементов. Список используемой литературы 1. Пуанкаре А. “О науке”.М., 1983 2. Аристотель “Сочинения”. М., “Мысль”, 1975 г. 3. Кант И. “Сочинения”, М., “Мысль”, 1964 г. 4. Н.К.Вахтомин “Теория научного знания Иммануила Канта”. М., “Наука”, 1986 г. 5. Кедров Б.М. “Предмет и взаимосвязь естественных наук”.М., “Наука”,1967.436с. 6.“Природа и общество” М, “Наука,1968.348с. 7.“Физика ХХ века. Развитие и перспективы.” Сборник. М,“Наука,1984.334с. 8.Алексеев И.С., Овчинников Н.Ф., Печенкин А.А. “Методология обоснования квантовой теории”. М.: “Наука”,1984.334с. 9.В.И.Кузнецов, Г.М.Идлис, В.Н.Гутина “Естествознание” М, “Агар”,1996,384с.