| | | | О.А. Мелихова В работе подробно рассмотрена суть логического вывода на основе нечеткой метаимпликации, с помощью примеров показана максиминная свертка нечетких отношений, используемая в моделях принятия решений и при распознавании нечетких образов. При выполнении нечетких выводов используются нечеткие соответствия R, заданные между одной проблемной областью (множество X) и другой областью (множество Y) в виде нечеткого подмножества прямого произведения 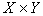 , определяемого по формуле [7,13]: , определяемого по формуле [7,13]: 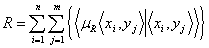 , (1.1) , (1.1)
где 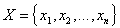 – область отправления, – область отправления,  – область прибытия, – область прибытия,  – функция принадлежности – функция принадлежности 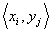 нечеткому соответствию R, а знак нечеткому соответствию R, а знак 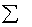 означает совокупность (объединение) множеств. означает совокупность (объединение) множеств. Если существует правило типа “если A, то B”, использующее нечеткие множества A 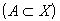 и B и B 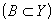 , то один из способов построения нечеткого соответствия R состоит в следующем: , то один из способов построения нечеткого соответствия R состоит в следующем: 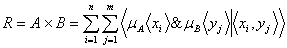
или  , (1.2) , (1.2)
где 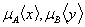 – функции принадлежности элементов x, y соответственно множествам A и B. – функции принадлежности элементов x, y соответственно множествам A и B. Пример 1. Пусть X и Y- области натуральных чисел от 1 до 4. Определим следующим образом нечеткие множества: A= “маленькие”, B= “большие”. X=Y={1,2,3,4}, т.е. для примера взят частный случай соответствия- отношение на множестве {1,2,3,4}:  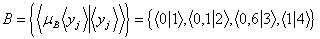 . .
Для примера “если x маленькое, то y большое” (или 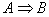 , где знак означает операцию нечеткой метаимпликации) можно построить нечеткое отношение R следующим образом: , где знак означает операцию нечеткой метаимпликации) можно построить нечеткое отношение R следующим образом: | | | y1 | y2 | y3 | y4 | | | x1 | 0 | 0,1 | 0,6 | 1 | | R= | x2 | 0 | 0,1 | 0,6 | 0,6 | | | x3 | 0 | 0,1 | 0,1 | 0,1 | | | x4 | 0 | 0 | 0 | 0 | В качестве элементов матрицы R записаны значения  , вычисленные по формуле (1.2). , вычисленные по формуле (1.2). Для свертки нечетких отношений чаще выбирается свертка max-min (максиминная композиция). Пусть R – нечеткое соответствие множества X и множества Y, а S – нечеткое соответствие множества Y и множества V. Тогда нечеткое соответствие между X и V определяется как свертка (композиция)  , где , где 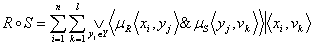
или  . (1.3) . (1.3)
Пример 2. Пусть  и заданы нечеткие множества A и заданы нечеткие множества A 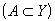 = “не маленькие”, H = “не маленькие”, H 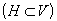 = “очень большие”, где = “очень большие”, где  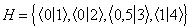 . .
Тогда для правила “если y не маленькое, то v очень большое” (или 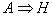 ), в соответствии с формулой (1.2) нечеткое соответствие S определяется как ), в соответствии с формулой (1.2) нечеткое соответствие S определяется как | | | v1 | v2 | v3 | v4 | | | y1 | 0 | 0 | 0 | 0 | | S= | y2 | 0 | 0 | 0,4 | 0,4 | | | y3 | 0 | 0 | 0,5 | 0,9 | | | y4 | 0 | 0 | 0,5 | 1 | Если теперь по формуле (1.3) вычислить свертку max-min с нечетким отношением R, полученным в примере 1.1, то из двух отношений: если x маленькое, то y большое, если y не маленькое, то v очень большое можно построить нечеткое отношение из X в V. 
| | | y1 | y2 | y3 | y4 | | | v1 | v2 | v3 | v4 | | | | x1 | 0 | 0,1 | 0,6 | 1 | | y1 | 0 | 0 | 0 | 0 | | | = | x2 | 0 | 0,1 | 0,6 | 0,6 | 
| y2 | 0 | 0 | 0,4 | 0,4 | = | | | x3 | 0 | 0,1 | 0,1 | 0,1 | | y3 | 0 | 0 | 0,5 | 0,9 | | | | x4 | 0 | 0 | 0 | 0 | | y4 | 0 | 0 | 0,5 | 1 | | | | | v1 | v2 | v3 | v4 | | | | x1 | 0 | 0 | 0,5 | 1 | | | = | x2 | 0 | 0 | 0,5 | 0,6 | | | | x3 | 0 | 0 | 0,1 | 0,1 | | | | x4 | 0 | 0 | 0 | 0 | | Модель принятия решений на основе композиционного правила вывода описывает связь всех возможных состояний сложной системы с управляющими решениями. Формально модель задается в виде тройки (X,R,Y), где 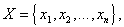  – базовые множества, на которых заданы, соответственно, входы – базовые множества, на которых заданы, соответственно, входы  и выходы и выходы 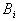 системы, R – нечеткое соответствие “вход-выход”. Соответствие R строится на основе словесной качественной информации специалиста (эксперта), путем непосредственной формализации его нечетких стратегий. Эксперт описывает особенности принятия решений при функционировании сложной системы в виде ряда высказываний типа “если системы, R – нечеткое соответствие “вход-выход”. Соответствие R строится на основе словесной качественной информации специалиста (эксперта), путем непосредственной формализации его нечетких стратегий. Эксперт описывает особенности принятия решений при функционировании сложной системы в виде ряда высказываний типа “если 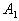 , то , то 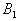 , иначе, если , иначе, если  , то , то 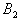 , иначе, ..., если , иначе, ..., если 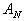 , то , то  ”. Здесь ”. Здесь 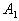 , ,  ,..., ,..., 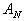 – нечеткие подмножества, определенные на базовом множестве X, а – нечеткие подмножества, определенные на базовом множестве X, а 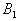 , , 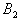 ,..., ,...,  – нечеткие подмножества из базового множества Y. Все эти нечеткие подмножества задаются функциями принадлежности – нечеткие подмножества из базового множества Y. Все эти нечеткие подмножества задаются функциями принадлежности  и и 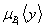 . . Способ построения нечеткого отношения связывает высказывания эксперта по правилу “если  , то , то 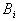 ” и определяется функцией принадлежности ” и определяется функцией принадлежности 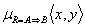 , получаемой по формуле (1.2). Связка “иначе” между правилами понимается как или-связка, поскольку общее нечеткое отношение состоит из: правило 1, или правило 2 , или, ..., или правило N. Поэтому общее отношение R формально определяется следующим образом: , получаемой по формуле (1.2). Связка “иначе” между правилами понимается как или-связка, поскольку общее нечеткое отношение состоит из: правило 1, или правило 2 , или, ..., или правило N. Поэтому общее отношение R формально определяется следующим образом: 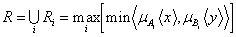 , где i=1,..., N. (1.4) , где i=1,..., N. (1.4)
Если предположить, что мы имеем нечеткое событие  , т.е. входную ситуацию, представленную нечетким подмножеством, и известно общее отношение R, тогда результирующее действие выводится по композиционному правилу вывода: , т.е. входную ситуацию, представленную нечетким подмножеством, и известно общее отношение R, тогда результирующее действие выводится по композиционному правилу вывода: 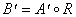 . Значение функции принадлежности для . Значение функции принадлежности для 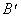 вычисляется посредством максиминной операции, определяемой уравнением вычисляется посредством максиминной операции, определяемой уравнением 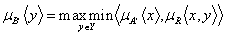 . (1.5) . (1.5)
Рассмотренный логический вывод на основе нечеткой обобщенной метаимпликации хорошо зарекомендовал себя при использовании в экспертных системах, а также при принятии решений в реальном масштабе времени в задачах управления и контроля. Список литературы Заде Л.А. Основы нового подхода к анализу сложных систем и процессов принятия решений. /М.: Математика сегодня, 1974, с.5-49. Дюбуа Д., Прад А. Теория возможностей. Приложения к представлению знаний в информатике. Пер. с франц. М.: Радио и связь, 1990, 288с.
|

