Реферат на тему Неравенства
Работа добавлена на сайт bukvasha.net: 2014-12-25Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Содержание
1) Основное понятие неравенства
2) Основные свойства числовых неравенств. Неравенства содержащие переменную.
3) Графическое решение неравенств второй степени
4) Системы неравенств. Неравенства и системы неравенств с двумя переменными.
5) Решение рациональных неравенств методом интервалов
6) Решение неравенств, содержащих переменную под знаком модуля
1. Основное понятие неравенства
Неравенство [inequality] — соотношение между числами (или любыми математическими выражениями, способными принимать численное значение), указывающее, какое из них больше или меньше другого. Над этими выражениями можно по определенным правилам производить следующие действия: сложение, вычитание, умножение и деление (причем при умножении или делении Н. на отрицательное число смысл его меняется на противоположный). Одно из основных понятий линейного программирования — линейные неравенства вида
a1x1+ a2x2 +... + anxn * b,
где a1,..., an, b — постоянные и знак * — один из знаков неравенства, напр. ≥, <, ≤.
В матричной алгебре знак ≥ означает что все элементы матрицы, расположенной слева, не меньше (а хотя бы часть из них больше) соответствующих элементов матрицы, расположенной справа. В отличие от этого знак ≤ означает, что все элементы левой матрицы не меньше соответствующих элементов правой матрицы; в частности, все соответствующие элементы могут быть попарно равны. (Иногда применяются и другие обозначения.)
· алгебраические
· трансцендентные
Алгебраические неравенства подразделяются на неравенства первой, второй, и т. д. степени.
Пример:
Неравенство 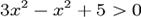 - алгебраическое, второй степени.
- алгебраическое, второй степени.
Неравенство 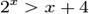 - трансцендентное.
- трансцендентное.
2. Основные свойства числовых неравенств. Неравенства содержащие переменную
1) Если a>b , b<a;
2) Если a>b b>c a>c;
3) Если a>b a+c>b+c;
4) Если a+b>c a> c-b;
5) Если обе части верного неравенства умножить на одно и то же положительное число, то получится верное неравенство;
6) Если обе части верного неравенства умножить на одно и то же число и изменить знак на противоположный, то получится верное неравенство;
7) Множество всех х, при которых имеют смысл выражения f(x) и g(x), называется областью определения неравенства f(x) >g(x);
8) Два неравенства, содержащие одну и ту же переменную, называются равносильными, если они имеют общее множество решений (множество решений этих неравенств совпадают);
9) Если к обеим частям неравенства прибавить(или вычесть) любую функцию J(x). область определения которой содержит область определения неравенств, то получится новое неравенств, равносильное данному;
10) Если обе части неравенства f(x) >g(x) умножить (или разделить) на любую функцию J(x), определенную для всех значений переменной х из области определения данного неравенства, сохраняющую постоянный знак и отличную от нуля, то при J(x)>0 получится неравенство, равносильное данном, а при J(x)<0 равносильным данному является неравенство противоположного знака.
Неравенства с одной переменной. Пусть дано неравенство f(x) >g(x). Всякое значение переменной, при котором данное неравенство с одной переменной обращается в верное числовое неравенство, называется решением неравенства с одной переменной. Решить неравенство с переменной - значит найти все его решения или доказать, что их нет.
Два неравенства с одной переменной называются равносильными, если решения этих неравенств совпадают.
3. Графическое решение неравенств второй степени
1) Графиком квадратичной функции y = ах2 +bх + с является парабола с ветвями, направленными вверх, если а > 0, и вниз, если а < 0 (иногда говорят, что парабола направлена выпуклостью вниз, если а > 0 и выпуклостью вверх, если а < 0). При этом возможны три случая:
2) Парабола пересекает ось 0х (т. е. уравнение ах2 + bх + с = 0 имеет два различных корня). То есть, если а<0 то решением неравенства является множество [x1;x2].
y = ах2 +bх + с a>0 D>0 y = ах2 +bх + с a<0 D>0,

Парабола имеет вершину на оси 0х (т. е. уравнение ах2 + х + с = 0 имеет один корень, так называемый двукратный корень) То есть, если d=0, то при a>0 решением неравенства служит вся числовая прямая, а при a<0 единственная точка х1, являющаяся единственным корнем квадратного трехчлена ах2 + х + с
y = ах2 +bх + с a>0 D=0 y = ах2 +bх + с a<0 D=0,

3) Если d<0 то график квадратного трехчлена f(x) = ах2 +bх + с не пересекает ось Ох и лежит выше этой оси при a>0 и ниже ее при a<0 В первом случае множество решений неравенства есть вся числовая прямая, а во втором оно является пустым.
4)
y = ах2 +bх + с a>0 D<0 y = ах2 +bх + с a<0 D<0,

4) Решить неравенство графическим способом
1) 3х2 -4х 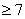
;
3х2-4х 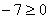
.
1. Пусть f(x) = 3х2 -4х - 7 тогда найдем такие х при которых f(x) 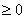
;
2. Найдем нули функции.
3х2-4х-7=0,
D=100,
Х=-1 Х=7\3.

f(x) 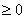
при х 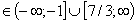
.
Ответ f(x) 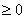
при х 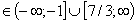
.
2) х2 >-4x-5;
x2 +4x +5>0;
Пусть f(x)=х2 +4х +5 тогда Найдем такие х при которых f(x)>0,
X2+4x+5=0,
D=-4 Нет нулей.

Ответ 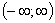
.
4. Системы неравенств. Неравенства и системы неравенств с двумя переменными
1) Множество решений системы неравенств есть пересечение множеств решений входящих в нее неравенств.
2) Множество решений неравенства f(х;у)>0 можно графически изобразить на координатной плоскости. Обычно линия, заданная уравнением f(х;у)=0 ,разбивает плоскость на 2 части, одна из которых является решением неравенства. Чтобы определить, какая из частей, надо подставить координаты произвольной точки М(х0;у0) , не лежащей на линии f(х;у)=0, в неравенство. Если f(х0;у0) > 0 , то решением неравенства является часть плоскости, содержащая точку М0. если f(х0;у0)<0, то другая часть плоскости.
3) Множество решений системы неравенств есть пересечение множеств решений входящих в нее неравенств. Пусть, например, задана система неравенств:
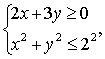
.
Для первого неравенства множество решений есть круг радиусом 2 и с центром в начале координат, а для второго- полуплоскость, расположенная над прямой 2х+3у=0. Множеством решений данной системы служит пересечение указанных множеств, т.е. полукруг.
4) Пример. Решить систему неравенств:
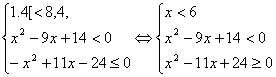
Решением 1-го неравенства служит множество 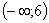
, 2-го множество (2;7) и третьего - множество 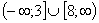
.
Пересечением указанных множеств является промежуток(2;3], который и есть множество решений системы неравенств.
5. Решение рациональных неравенств методом интервалов
В основе метода интервалов лежит следующее свойство двучлена (х-а): точка х=α делит числовую ось на две части — справа от точки α двучлен (х‑α)>0, а слева от точки α (х-α)<0.
Пусть требуется решить неравенство (x-α1)(x-α2)...(x-αn)>0, где α1, α2...αn-1, αn — фиксированные числа, среди которых нет равных, причем такие, что α1 < α2 <...< αn-1 < αn. Для решения неравенства (x-α1)(x-α2)...(x‑αn)>0 методом интервалов поступают следующим образом: на числовую ось наносят числа α1, α2...αn-1, αn; в промежутке справа от наибольшего из них, т.е. числа αn, ставят знак «плюс», в следующем за ним справа налево интервале ставят знак «минус», затем — знак «плюс», затем знак «минус» и т.д. Тогда множество всех решений неравенства (x-α1)(x‑α2)...(x-αn)>0 будет объединение всех промежутков, в которых поставлен знак «плюс», а множество решений неравенства (x-α1)(x-α2)...(x‑αn)<0 будет объединение всех промежутков, в которых поставлен знак «минус».
1) Решение рациональных неравенств (т.е неравенств вида 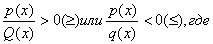
P(x) Q(x) где – многочлены) основано на следующем свойстве непрерывной функции: если непрерывная функция обращается в нуль в точках х1 и х2 (х1;х2) и между этими точками не имеет других корней, то в промежутках(х1;х2) функция сохраняет свой знак.
Поэтому для нахождения промежутков знакопостоянства функции y=f(x) на числовой прямой отмечают все точки, в которых функция f(x) обращается в нуль или терпит разрыв. Эти точки разбивают числовую прямую на несколько промежутков, внутри каждого из которых функция f(x) непрерывна и не обращается в нуль, т.е. сохраняет знак. Чтобы определить этот знак, достаточно найти знак функции в какой либо точке рассматриваемого промежутка числовой прямой.
2) Для определения интервалов знакопостоянства рациональной функции, т.е. Для решения рационального неравенства, отмечаем на числовой прямой корни числителя и корни знаменателя, которые как и являются корнями и точками разрыва рациональной функции.
Решение неравенств методом интервалов
3. 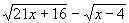 < 20.
< 20.
Решение. Область допустимых значений определяется системой неравенств:
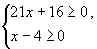 .
.
Для функции f(x) = 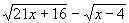 – 20. Находим f(x):
– 20. Находим f(x):
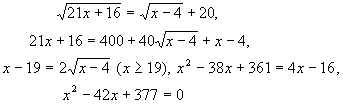
откуда x = 29 и x = 13.
f(30) = 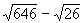 – 20 = 0,3 > 0,
– 20 = 0,3 > 0,
f(5) = 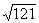 – 1 – 20 = – 10 < 0.
– 1 – 20 = – 10 < 0.
Ответ: [4; 29).
х2+х-2 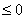
Пусть f(x)=х2+х-2 тогда найдем такие х при которых f(x)<0.
Найдем нули х=1, х=-2.
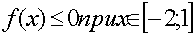
х3-4х<0
x(x2-4)<0
x(x-2)(x+2)<0
x=0 x=2 x=-2
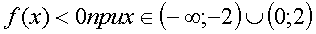
6. Решение неравенств, содержащих переменную под знаком модуля
Решение неравенства, содержащего выражение 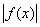
, приводит к рассмотрению двух случаев:
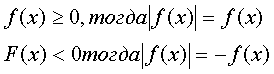
Можно воспользоваться геометрической интерпретацией модуля действительного числа, согласно которой |a| означает расстояние точки а координатной прямой от начала отсчета О, а |a-b| означает расстояние между точками а и b на координатной прямой.
Можно использовать метод возведения в квадрат обеих частей неравенства, основанный на следующей теореме. Если выражения f(x) и g(x) при любых х принимают только неотрицательные значения, то неравенства f(x)>g(x) и (f(x))2>(g(x))2 равносильны.
Можно использовать свойства неравенств, содержащих переменную под знаком модуля:
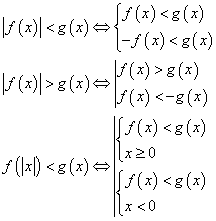
Решить неравенство:
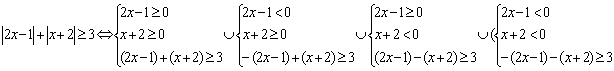
.
Объединяя результаты получим 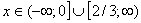
.
1) Основное понятие неравенства
2) Основные свойства числовых неравенств. Неравенства содержащие переменную.
3) Графическое решение неравенств второй степени
4) Системы неравенств. Неравенства и системы неравенств с двумя переменными.
5) Решение рациональных неравенств методом интервалов
6) Решение неравенств, содержащих переменную под знаком модуля
1. Основное понятие неравенства
Неравенство [inequality] — соотношение между числами (или любыми математическими выражениями, способными принимать численное значение), указывающее, какое из них больше или меньше другого. Над этими выражениями можно по определенным правилам производить следующие действия: сложение, вычитание, умножение и деление (причем при умножении или делении Н. на отрицательное число смысл его меняется на противоположный). Одно из основных понятий линейного программирования — линейные неравенства вида
a1x1+ a2x2 +... + anxn * b,
где a1,..., an, b — постоянные и знак * — один из знаков неравенства, напр. ≥, <, ≤.
В матричной алгебре знак ≥ означает что все элементы матрицы, расположенной слева, не меньше (а хотя бы часть из них больше) соответствующих элементов матрицы, расположенной справа. В отличие от этого знак ≤ означает, что все элементы левой матрицы не меньше соответствующих элементов правой матрицы; в частности, все соответствующие элементы могут быть попарно равны. (Иногда применяются и другие обозначения.)
Классификация неравенств
Неравенства, содержащие неизвестные величины, подразделяются на:[1]· алгебраические
· трансцендентные
Алгебраические неравенства подразделяются на неравенства первой, второй, и т. д. степени.
Пример:
Неравенство
Неравенство
2. Основные свойства числовых неравенств. Неравенства содержащие переменную
1) Если a>b , b<a;
2) Если a>b b>c a>c;
3) Если a>b a+c>b+c;
4) Если a+b>c a> c-b;
5) Если обе части верного неравенства умножить на одно и то же положительное число, то получится верное неравенство;
6) Если обе части верного неравенства умножить на одно и то же число и изменить знак на противоположный, то получится верное неравенство;
7) Множество всех х, при которых имеют смысл выражения f(x) и g(x), называется областью определения неравенства f(x) >g(x);
8) Два неравенства, содержащие одну и ту же переменную, называются равносильными, если они имеют общее множество решений (множество решений этих неравенств совпадают);
9) Если к обеим частям неравенства прибавить(или вычесть) любую функцию J(x). область определения которой содержит область определения неравенств, то получится новое неравенств, равносильное данному;
10) Если обе части неравенства f(x) >g(x) умножить (или разделить) на любую функцию J(x), определенную для всех значений переменной х из области определения данного неравенства, сохраняющую постоянный знак и отличную от нуля, то при J(x)>0 получится неравенство, равносильное данном, а при J(x)<0 равносильным данному является неравенство противоположного знака.
Неравенства с одной переменной. Пусть дано неравенство f(x) >g(x). Всякое значение переменной, при котором данное неравенство с одной переменной обращается в верное числовое неравенство, называется решением неравенства с одной переменной. Решить неравенство с переменной - значит найти все его решения или доказать, что их нет.
Два неравенства с одной переменной называются равносильными, если решения этих неравенств совпадают.
3. Графическое решение неравенств второй степени
1) Графиком квадратичной функции y = ах2 +bх + с является парабола с ветвями, направленными вверх, если а > 0, и вниз, если а < 0 (иногда говорят, что парабола направлена выпуклостью вниз, если а > 0 и выпуклостью вверх, если а < 0). При этом возможны три случая:
2) Парабола пересекает ось 0х (т. е. уравнение ах2 + bх + с = 0 имеет два различных корня). То есть, если а<0 то решением неравенства является множество [x1;x2].
y = ах2 +bх + с a>0 D>0 y = ах2 +bх + с a<0 D>0,

Парабола имеет вершину на оси 0х (т. е. уравнение ах2 + х + с = 0 имеет один корень, так называемый двукратный корень) То есть, если d=0, то при a>0 решением неравенства служит вся числовая прямая, а при a<0 единственная точка х1, являющаяся единственным корнем квадратного трехчлена ах2 + х + с
y = ах2 +bх + с a>0 D=0 y = ах2 +bх + с a<0 D=0,

3) Если d<0 то график квадратного трехчлена f(x) = ах2 +bх + с не пересекает ось Ох и лежит выше этой оси при a>0 и ниже ее при a<0 В первом случае множество решений неравенства есть вся числовая прямая, а во втором оно является пустым.
4)
y = ах2 +bх + с a>0 D<0 y = ах2 +bх + с a<0 D<0,

4) Решить неравенство графическим способом
1) 3х2 -4х
3х2-4х
1. Пусть f(x) = 3х2 -4х - 7 тогда найдем такие х при которых f(x)
2. Найдем нули функции.
3х2-4х-7=0,
D=100,
Х=-1 Х=7\3.

f(x)
Ответ f(x)
2) х2 >-4x-5;
x2 +4x +5>0;
Пусть f(x)=х2 +4х +5 тогда Найдем такие х при которых f(x)>0,
X2+4x+5=0,
D=-4 Нет нулей.

Ответ
4. Системы неравенств. Неравенства и системы неравенств с двумя переменными
1) Множество решений системы неравенств есть пересечение множеств решений входящих в нее неравенств.
2) Множество решений неравенства f(х;у)>0 можно графически изобразить на координатной плоскости. Обычно линия, заданная уравнением f(х;у)=0 ,разбивает плоскость на 2 части, одна из которых является решением неравенства. Чтобы определить, какая из частей, надо подставить координаты произвольной точки М(х0;у0) , не лежащей на линии f(х;у)=0, в неравенство. Если f(х0;у0) > 0 , то решением неравенства является часть плоскости, содержащая точку М0. если f(х0;у0)<0, то другая часть плоскости.
3) Множество решений системы неравенств есть пересечение множеств решений входящих в нее неравенств. Пусть, например, задана система неравенств:
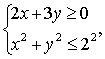
Для первого неравенства множество решений есть круг радиусом 2 и с центром в начале координат, а для второго- полуплоскость, расположенная над прямой 2х+3у=0. Множеством решений данной системы служит пересечение указанных множеств, т.е. полукруг.
4) Пример. Решить систему неравенств:
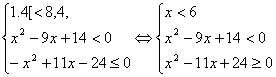
Решением 1-го неравенства служит множество
Пересечением указанных множеств является промежуток(2;3], который и есть множество решений системы неравенств.
5. Решение рациональных неравенств методом интервалов
В основе метода интервалов лежит следующее свойство двучлена (х-а): точка х=α делит числовую ось на две части — справа от точки α двучлен (х‑α)>0, а слева от точки α (х-α)<0.
Пусть требуется решить неравенство (x-α1)(x-α2)...(x-αn)>0, где α1, α2...αn-1, αn — фиксированные числа, среди которых нет равных, причем такие, что α1 < α2 <...< αn-1 < αn. Для решения неравенства (x-α1)(x-α2)...(x‑αn)>0 методом интервалов поступают следующим образом: на числовую ось наносят числа α1, α2...αn-1, αn; в промежутке справа от наибольшего из них, т.е. числа αn, ставят знак «плюс», в следующем за ним справа налево интервале ставят знак «минус», затем — знак «плюс», затем знак «минус» и т.д. Тогда множество всех решений неравенства (x-α1)(x‑α2)...(x-αn)>0 будет объединение всех промежутков, в которых поставлен знак «плюс», а множество решений неравенства (x-α1)(x-α2)...(x‑αn)<0 будет объединение всех промежутков, в которых поставлен знак «минус».
1) Решение рациональных неравенств (т.е неравенств вида
Поэтому для нахождения промежутков знакопостоянства функции y=f(x) на числовой прямой отмечают все точки, в которых функция f(x) обращается в нуль или терпит разрыв. Эти точки разбивают числовую прямую на несколько промежутков, внутри каждого из которых функция f(x) непрерывна и не обращается в нуль, т.е. сохраняет знак. Чтобы определить этот знак, достаточно найти знак функции в какой либо точке рассматриваемого промежутка числовой прямой.
2) Для определения интервалов знакопостоянства рациональной функции, т.е. Для решения рационального неравенства, отмечаем на числовой прямой корни числителя и корни знаменателя, которые как и являются корнями и точками разрыва рациональной функции.
Решение неравенств методом интервалов
3.
Решение. Область допустимых значений определяется системой неравенств:
Для функции f(x) =
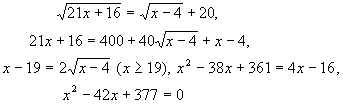
откуда x = 29 и x = 13.
f(30) =
f(5) =
Ответ: [4; 29).
х2+х-2
Пусть f(x)=х2+х-2 тогда найдем такие х при которых f(x)<0.
Найдем нули х=1, х=-2.
х3-4х<0
x(x2-4)<0
x(x-2)(x+2)<0
x=0 x=2 x=-2
6. Решение неравенств, содержащих переменную под знаком модуля
Решение неравенства, содержащего выражение
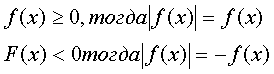
Можно воспользоваться геометрической интерпретацией модуля действительного числа, согласно которой |a| означает расстояние точки а координатной прямой от начала отсчета О, а |a-b| означает расстояние между точками а и b на координатной прямой.
Можно использовать метод возведения в квадрат обеих частей неравенства, основанный на следующей теореме. Если выражения f(x) и g(x) при любых х принимают только неотрицательные значения, то неравенства f(x)>g(x) и (f(x))2>(g(x))2 равносильны.
Можно использовать свойства неравенств, содержащих переменную под знаком модуля:
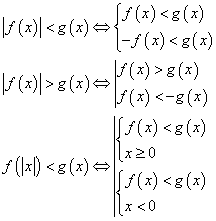
Решить неравенство:
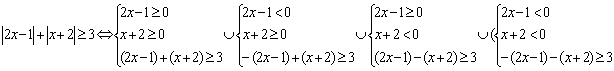
Объединяя результаты получим