Диплом на тему Диалектика развития понятия функции в школьном курсе математики
Работа добавлена на сайт bukvasha.net: 2015-06-24Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФАКУЛЬТЕТ МАТЕМАТИКИ И КОМПЬЮТЕРНЫХ НАУК
Диалектика развития понятия функции в школьном курсе математики
(дипломная работа)
Т – 2004
Введение
Глава I. Определение понятия функция
§ 1.1. Краткий обзор понятия числа.
§ 1.2. История развития функции.
§ 1.3. Различные современные подходы к определению понятия «функция», графики функции.
§ 1.4. Графики функции.
§ 1.5. Основные свойства функции.
п.1.5.1. Ограниченность.
п.1.5.2. Четность, нечетность.
п.1.5.3. Монотонность.
п.1.5.4. Точки экстремума.
п.1.5.5. Непрерывность.
п.1.5.6. Периодичность.
Глава II. Понятие функции в школьном курсе.
§ 2.1. Линейная функция.
§ 2.2. Квадратичная функция.
§ 2.3. Обратная пропорциональность.
§ 2.4. Степенная функция.
§ 2.5. Показательная функция.
§ 2.6. Логарифмическая функция.
§ 2.7. Тригонометрическая функция.
Глава III. Вспомогательные приемы построения усложненных графиков.
§ 3.1. Параллельный перенос.
п.3.1.1. Сдвиг оси х-ов.
п.3.1.2. Сдвиг оси у-ов.
§ 3.2. Растяжение и сжатие графика
п.3.2.1. По оси х-ов.
п.3.2.2. По оси у-ов.
§ 3.3. Отражение.
§ 3.4. График суммы и разности двух функций.
§ 3.5. Графики произведения и частного двух функций.
Заключение
Список использованных источников и литературы
Глава I. Определение понятия функция.
§ 1.1. Краткий обзор развития понятия числа.
На первых этапах существования человеческого общества числа, открытые в процессе практической деятельности, служили для примитивного счета предметов, дней, шагов и тому подобного. В первобытном обществе человек нуждался лишь в нескольких первых числах. Но с развитием цивилизации ему потребовалось изобретать все большие и большие числа. Этот процесс продолжался на протяжении многих столетий и потребовал напряженного интеллектуального труда.
С зарождением обмена продуктами труда у людей появилась необходимость сравнивать число предметов одного вида с числом предметов другого вида. На этом этапе возникли понятия “больше”, “меньше”, “столько же” или “равно”. Вероятно, на этом же этапе развития люди стали складывать числа. Значительно позже они научились вычитать числа, затем умножать и делить их. Даже в средние века деление чисел считалось очень сложным и служило признаком чрезвычайно высокой образованности человека.
С открытием действий с числами или операций над ними возникла наука арифметика. Ее возникновению и развитию способствовали практические потребности - строительство разнообразных сооружений, торговля и мореходство. Долгое время в арифметике имели дело с числами относительно небольшими. Например, в системе счисления Древней Греции самым большим числом, которое имело название, была “мириада” - 10 000. Еще в III в. до н. э. люди не знали, что натуральный ряд чисел бесконечен. Вот тогда-то Архимед (около 287-212 до н.э.) в своем трактате “Исчисление песчинок” - “Псаммит” разработал систему, которая позволяла выразить сколь угодно большое число, и показал, что натуральный ряд чисел был бесконечен.
Математики Древней Греции, занявшись проблемами больших чисел, совершили скачок от конечного к бесконечному. Смелая идея бесконечности, которая шла вразрез с философскими воззрениями о конечности Вселенной, открыла в математике широкие возможности, хотя и вызвала значительные противоречия, некоторые из них не раскрыты и по сей день.
В IV в. до н. э. греческие математики из школы Пифагора открыли несоизмеримые отрезки, длины которых они не могли выразить ни целым, ни дробным числом. Одним из таких отрезков была диагональ квадрата со сторонами, равными единице. Теперь длину такого отрезка мы выражаем через 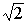
. Ученые того времени относили к числам только рациональные и не признавали иррациональные числа. Они нашли выход в том, что под числами стали понимать длины отрезков прямых.
Геометрическое выражение чисел на первых этапах сыграло положительную роль в дальнейшем продвижении математики, но затем вызвало ряд затруднений и стало тормозом в прогрессе арифметики и алгебры.
Потребовалась не одна сотня лет для того, чтобы математики смогли осмыслить понятие иррационального числа и выработать способ записи такого числа и приближенного значения его в виде бесконечной десятичной дроби.
Таким образом, понятие числа прошло длинный путь развития: сначала целые числа, затем дробные, рациональные (положительные и отрицательные) и, наконец, действительные. Но на этом развитие не завершилось. В связи с решением уравнений математики встретились с числом, которое выражалось 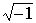
. Оно получило название мнимой единицы. Долгое время мнимые числа не признавались за числа. После того как норвежский математик Гаспар Вессель (1745-1818) нашел возможность представить мнимое число геометрически, то так называемые “мнимые числа” получили свое место в множестве комплексных чисел. Однако и раньше интерпретация этих чисел имелась у Даламбера (1717-1783) и Эйлера (1707-1783), которые ставили в соответствие комплексным числам точки плоскости и некоторые функции комплексного переменного истолковывали геометрически.
Обозначение комплексного числа а+b 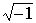
принадлежит Кардано (1501-1576). Эйлер стал записывать это число в виде а+bi, где i= 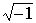
, а i2=-1. По рекомендации ирландского математика Уильяма Роуэна Гамильтона (1805—1865) комплексные числа стали выражать парой действительных чисел в виде (а, b). Однако и на этом развитие понятия числа не завершилось. Оно продолжает свой путь дальше.
(1858-1932) в статье «О понятии числа», опубликованной в 1891 г. Вот как формулировал Пеано свои пять аксиом:
1. О есть натуральное число.
2. Следующее за натуральным числом есть натуральное число.
3. О не следует ни за каким натуральным числом.
4. Всякое натуральное число следует только за одним натуральным числом.
5. Аксиома полной индукции: если какое-либо предложение доказано для 1 и если из допущения, что оно верно для натурального числа n, вытекает, что оно верно для следующего за n натурального числа, то это предложение верно для всех натуральных чисел.
Итак, с аксиоматической точки зрения мы имеем дело с двумя основными понятиями: «натуральные числа» (объект) и «непосредственно следует за» (соотношение). Эти понятия косвенно определяются системой аксиом.
Излагаемая в настоящее время в учебных руководствах система аксиом натуральных чисел лишь по форме несколько отличается от вышеприведенной. Натуральные числа — это элементы всякого непустого множества N, в котором для некоторых элементов а и b установлено отношение «b следует за а» (число, следующее за а, обозначается а*), удовлетворяющее следующим четырем аксиомам:
1. Существует натуральное число 1, непосредственно не следующее ни за каким натуральным числом, т. е. для любого а имеем: а*¹1.
2. Для каждого натурального числа а существует одно и только одно непосредственно за ним следующее натуральное число а*, т.е. а = b ® а* = b*.
3. Любое натуральное число, кроме 1, непосредственно следует за одним и только одним натуральным числом, т. е. если а¹1, то из а*=b*®а=b.
4. Аксиома индукции. Пусть М — подмножество множества N натуральных чисел, обладающее свойствами: а) 1 принадлежит М, б) если натуральное число а принадлежит М, то а* также принадлежит М; тогда множество М содержит все натуральные числа, т.е. М совпадает с N.
То, что в первоначальной формулировке (Пеано) первый элемент есть 0, а не 1, не имеет принципиального значения. Дело в том, что в настоящее время нуль причисляется не к натуральным, а к целым числам. Символы 1, 2, 3, ..., которыми обычно обозначают натуральные числа, были выработаны, как мы уже знаем, на протяжении веков. На основе аксиом 1—4 можно определить арифметические действия и построить всю арифметику натуральных чисел чисто дедуктивным путем. В частности, на основе аксиомы 4 доказывается следующее предложение: если некоторая теорема Т, в формулировку которой входит натуральное число n, верна для n=1 и в предположении, что она верна для n, будет верна и для n+1, то Т верна для любого натурального числа. Это предложение, эквивалентное аксиоме 4, называют принципом математической индукции. На этом принципе и основан метод математической индукции, с помощью которого доказывают многие теоремы арифметики, алгебры, теории чисел и геометрии. Под индукцией (от латинского inductio — наведение) понимают в логике одну из форм умозаключений, состоящую в выведении общего суждения относительно бесконечного множества объектов на основании изучения некоторого конечного числа частных случаев.
Возникновение и применение идеи бесконечности в древнегреческой математике
Идея бесконечности возникла еще в глубокой древности в связи с представлениями о Вселенной. В философии под бесконечностью понимают отсутствие начала и конца во времени и в пространстве. Конечное и бесконечное — это две категории, т. е. два основных понятия, выражающие неразрывно связанные между собой противоположные стороны объективного мира. Вселенная, природа бесконечны. Бесконечная движущаяся материя существует в виде бесконечного многообразия взаимосвязанных конечных вещей. С понятием бесконечности в философии связано и математическое понятие бесконечности как одной из математических абстракций. Оно встречается уже на первых ступенях изучения арифметики, а именно когда речь идет о натуральном ряде чисел: 1, 2, 3, 4, .... В геометрии мы сталкиваемся с понятием бесконечности, когда прямая мыслится как бесконечная прямая и т. п.
Как известно, математика превратилась в дедуктивную науку в Древней Греции, где ее развитие протекало в сотрудничестве с философией. Уже в VI в. до н. э. греческие философы разрабатывали проблему бесконечности и связанную с ней проблему непрерывного и дискретного. Этими проблемами занимались представители милетской школы Анаксимандр (около 610—546 гг. до н. э.) в своем произведении «Апейрон» («Беспредельное»), Анаксимен (около 588гг. до н. э.) в сочинении «О природе». Такое же заглавие выбрал для одного из своих сочинений Анаксагор (около 500—428 гг. до н. э.), в котором он понятие бесконечности положил в основу своего мировоззрения. Анаксагор писал: «Среди малых величин не существует наименьшей, но уменьшение идет непрерывно». Эту мысль он дополнил, написав, что «всегда имеется нечто большее, чем то, что большое». Вот почему историки математики считают, что Анаксагор впервые ввел в математику понятие потенциально бесконечно малого и бесконечно большого, а это оказалось весьма существенным для дальнейшего развития математики. Но если Анаксагор и другие математики приписывали пространству только непрерывные свойства, то другие ученые создали представление о пространстве как о множестве точек, являющихся неделимыми элементами. Последняя концепция отвечала, в частности, духу школы Пифагора, в которой развивалось учение о дискретных (т. е. прерывных) объектах, а именно о числах. Пифагорейцы долгое время считали возможным распространить свое учение о целочисленной основе всего существующего и на геометрические величины. Открытие несоизмеримости, которое явно показало различие между дискретной природой (рациональных) чисел и непрерывной природой геометрических величин, привело, как известно, к большим трудностям, связанным с понятием бесконечности, к настоящему кризису в обосновании математики.
С точки зрения диалектического материализма в объективном реальном мире дискретное и непрерывное, движение и покой находятся в диалектическом единстве. Но нельзя отобразить движение, не остановив его, т.е. не прибегая к покою — его противоположности.
В настоящее время в основе изучения геометрии и математического анализа лежит понятие о вещественном числе. Множество вещественных чисел, как и множество точек прямой, обладает свойством непрерывности. Вещественным числом можно выразить отношение двух любых однородных величин. Однако, как известно, расширение понятия числа до вещественного и обоснование соответствующей теории были завершены только в XIX в.. Греки же, которые при открытии несоизмеримости имели представление лишь о дискретном множестве чисел (натуральных и в лучшем случае положительных рациональных), пошли в V—VI вв. по пути геометризации арифметики и строили общую теорию отношений, аналогичную нашей теории вещественных чисел, применяя ее к учению о подобии, к вопросам измерения площадей и объемов и вообще к исследованию непрерывных величин.
Изложим вкратце суть евдоксовой общей теории отношений (величин), содержащейся в V книге «Начал» Евклида (конец IV – III в. до н. э.). Величины здесь изображены отрезками, причем предполагается, что для любой пары величин найдется соответствующая пара отрезков а, b так, что отношение величин будет равно отношению отрезков а:b. В самом начале V книги вводится так называемая аксиома Архимеда, которую правильнее было бы называть аксиомой Евдокса (около 408 - около 355 до н. э.), или аксиомой Евдокса — Архимеда. Две однородные величины могут находиться в математическом отношении, только если на них распространяется эта аксиома которая является одной из аксиом непрерывности.
Равенство отношений определяется следующим образом: величины А, В имеют то же отношение, что и величины С, D, если для любой пары натуральных чисел тип выполняется какое-либо из следующих трех условий:
1) тА<пВ и тС<пD;
2) тА = пВ и тС = пD;
3) тА>пВ и тC>пD.
Современной операции умножения вещественных чисел у Евдокса соответствует составление отношений. «Составить» пару отношений А:В и В:С — значит найти отношение А:С, «составленное». Чтобы составить произвольные два отношения а:b и с:d, требуется предварительно найти отношение b:x, равное с:d, что осуществляется путем построения к любым трем отрезкам с, d, b четвертого пропорционального отрезка x. В V книге устанавливаются основные свойства отношений и их составления. Вышеприведенное определение отношений было, вероятно, подсказано Евдоксу как свойствами отношений соизмеримых величин, так и рассмотрением процесса измерения непрерывных геометрических величин. Целесообразность этого определения, конечно, можно проверить на разных примерах. О том, что некоторые математики неправильно его понимали, свидетельствует случай с французским ученым XVI в. П. Рамусом. Последний, возражавший против определения равенства отношений Евдокса, ссылался на следующий пример. Для чисел 4; 3 и 5; 4, т=6, п=9 имеет место неравенство
6·4<9·3 и 6·5<9·4,
но вместе с этим отношение 4:3 не равно отношению 5:4. Рамус не учел, что речь идет не об определенной одной паре или о конечном числе пар натуральных чисел т, п, а о произвольной паре. Достаточно в данном случае взять т=6, п=8, чтобы получить:
6·4=8·3,
в то время как 6·5<8·4.
Именно тот факт, что равенство отношений определяется Евдоксом с помощью бесконечного множества неравенств типа 1) или 3), вызывал много трудностей для понимания его теории, предвосхитившей теорию вещественных чисел Дедекинда (1831-1916). И метод исчерпывания Евдокса основывается на идее неограниченного приближения к некоторой величине с помощью последовательности неограниченного числа значений других величин и на основе безграничного деления любой величины на части, меньшие любых наперед заданных величин, т. е. в конечном итоге на идее потенциальной бесконечности, на которой базируется и метод пределов, которым пользуемся и мы. С помощью метода исчерпывания Евдокс строго доказал, что объем пирамиды равен 1/3 объема призмы с тем же основанием и высотой и другие предложения.
В итоге можно сказать, что идея бесконечности возникла и применялась в древнегреческой математике главным образом в связи с развитием арифметики и теории чисел (натуральный ряд, бесконечное множество простых чисел и др.), с открытием несоизмеримости и с вопросами измерения и исследования свойств геометрических фигур, рассматриваемых как непрерывные. ФАКУЛЬТЕТ МАТЕМАТИКИ И КОМПЬЮТЕРНЫХ НАУК
Диалектика развития понятия функции в школьном курсе математики
(дипломная работа)
Т – 2004
Введение
Глава I. Определение понятия функция
§ 1.1. Краткий обзор понятия числа.
§ 1.2. История развития функции.
§ 1.3. Различные современные подходы к определению понятия «функция», графики функции.
§ 1.4. Графики функции.
§ 1.5. Основные свойства функции.
п.1.5.1. Ограниченность.
п.1.5.2. Четность, нечетность.
п.1.5.3. Монотонность.
п.1.5.4. Точки экстремума.
п.1.5.5. Непрерывность.
п.1.5.6. Периодичность.
Глава II. Понятие функции в школьном курсе.
§ 2.1. Линейная функция.
§ 2.2. Квадратичная функция.
§ 2.3. Обратная пропорциональность.
§ 2.4. Степенная функция.
§ 2.5. Показательная функция.
§ 2.6. Логарифмическая функция.
§ 2.7. Тригонометрическая функция.
Глава III. Вспомогательные приемы построения усложненных графиков.
§ 3.1. Параллельный перенос.
п.3.1.1. Сдвиг оси х-ов.
п.3.1.2. Сдвиг оси у-ов.
§ 3.2. Растяжение и сжатие графика
п.3.2.1. По оси х-ов.
п.3.2.2. По оси у-ов.
§ 3.3. Отражение.
§ 3.4. График суммы и разности двух функций.
§ 3.5. Графики произведения и частного двух функций.
Заключение
Список использованных источников и литературы
Глава I. Определение понятия функция.
§ 1.1. Краткий обзор развития понятия числа.
На первых этапах существования человеческого общества числа, открытые в процессе практической деятельности, служили для примитивного счета предметов, дней, шагов и тому подобного. В первобытном обществе человек нуждался лишь в нескольких первых числах. Но с развитием цивилизации ему потребовалось изобретать все большие и большие числа. Этот процесс продолжался на протяжении многих столетий и потребовал напряженного интеллектуального труда.
С зарождением обмена продуктами труда у людей появилась необходимость сравнивать число предметов одного вида с числом предметов другого вида. На этом этапе возникли понятия “больше”, “меньше”, “столько же” или “равно”. Вероятно, на этом же этапе развития люди стали складывать числа. Значительно позже они научились вычитать числа, затем умножать и делить их. Даже в средние века деление чисел считалось очень сложным и служило признаком чрезвычайно высокой образованности человека.
С открытием действий с числами или операций над ними возникла наука арифметика. Ее возникновению и развитию способствовали практические потребности - строительство разнообразных сооружений, торговля и мореходство. Долгое время в арифметике имели дело с числами относительно небольшими. Например, в системе счисления Древней Греции самым большим числом, которое имело название, была “мириада” - 10 000. Еще в III в. до н. э. люди не знали, что натуральный ряд чисел бесконечен. Вот тогда-то Архимед (около 287-212 до н.э.) в своем трактате “Исчисление песчинок” - “Псаммит” разработал систему, которая позволяла выразить сколь угодно большое число, и показал, что натуральный ряд чисел был бесконечен.
Математики Древней Греции, занявшись проблемами больших чисел, совершили скачок от конечного к бесконечному. Смелая идея бесконечности, которая шла вразрез с философскими воззрениями о конечности Вселенной, открыла в математике широкие возможности, хотя и вызвала значительные противоречия, некоторые из них не раскрыты и по сей день.
В IV в. до н. э. греческие математики из школы Пифагора открыли несоизмеримые отрезки, длины которых они не могли выразить ни целым, ни дробным числом. Одним из таких отрезков была диагональ квадрата со сторонами, равными единице. Теперь длину такого отрезка мы выражаем через
Геометрическое выражение чисел на первых этапах сыграло положительную роль в дальнейшем продвижении математики, но затем вызвало ряд затруднений и стало тормозом в прогрессе арифметики и алгебры.
Потребовалась не одна сотня лет для того, чтобы математики смогли осмыслить понятие иррационального числа и выработать способ записи такого числа и приближенного значения его в виде бесконечной десятичной дроби.
Таким образом, понятие числа прошло длинный путь развития: сначала целые числа, затем дробные, рациональные (положительные и отрицательные) и, наконец, действительные. Но на этом развитие не завершилось. В связи с решением уравнений математики встретились с числом, которое выражалось
Обозначение комплексного числа а+b
Аксиомы натуральных чисел
Как известно, аксиоматическое построение любой математической теории начинается с перечисления неопределяемых, основных понятий (объектов и отношений) и аксиом, которым должны удовлетворять основные понятия. Вошедшая во всеобщее употребление система аксиом натуральных чисел была предложена итальянским математиком и логиком, профессором Туринского университета Джузеппе Пеано(1858-1932) в статье «О понятии числа», опубликованной в 1891 г. Вот как формулировал Пеано свои пять аксиом:
1. О есть натуральное число.
2. Следующее за натуральным числом есть натуральное число.
3. О не следует ни за каким натуральным числом.
4. Всякое натуральное число следует только за одним натуральным числом.
5. Аксиома полной индукции: если какое-либо предложение доказано для 1 и если из допущения, что оно верно для натурального числа n, вытекает, что оно верно для следующего за n натурального числа, то это предложение верно для всех натуральных чисел.
Итак, с аксиоматической точки зрения мы имеем дело с двумя основными понятиями: «натуральные числа» (объект) и «непосредственно следует за» (соотношение). Эти понятия косвенно определяются системой аксиом.
Излагаемая в настоящее время в учебных руководствах система аксиом натуральных чисел лишь по форме несколько отличается от вышеприведенной. Натуральные числа — это элементы всякого непустого множества N, в котором для некоторых элементов а и b установлено отношение «b следует за а» (число, следующее за а, обозначается а*), удовлетворяющее следующим четырем аксиомам:
1. Существует натуральное число 1, непосредственно не следующее ни за каким натуральным числом, т. е. для любого а имеем: а*¹1.
2. Для каждого натурального числа а существует одно и только одно непосредственно за ним следующее натуральное число а*, т.е. а = b ® а* = b*.
3. Любое натуральное число, кроме 1, непосредственно следует за одним и только одним натуральным числом, т. е. если а¹1, то из а*=b*®а=b.
4. Аксиома индукции. Пусть М — подмножество множества N натуральных чисел, обладающее свойствами: а) 1 принадлежит М, б) если натуральное число а принадлежит М, то а* также принадлежит М; тогда множество М содержит все натуральные числа, т.е. М совпадает с N.
То, что в первоначальной формулировке (Пеано) первый элемент есть 0, а не 1, не имеет принципиального значения. Дело в том, что в настоящее время нуль причисляется не к натуральным, а к целым числам. Символы 1, 2, 3, ..., которыми обычно обозначают натуральные числа, были выработаны, как мы уже знаем, на протяжении веков. На основе аксиом 1—4 можно определить арифметические действия и построить всю арифметику натуральных чисел чисто дедуктивным путем. В частности, на основе аксиомы 4 доказывается следующее предложение: если некоторая теорема Т, в формулировку которой входит натуральное число n, верна для n=1 и в предположении, что она верна для n, будет верна и для n+1, то Т верна для любого натурального числа. Это предложение, эквивалентное аксиоме 4, называют принципом математической индукции. На этом принципе и основан метод математической индукции, с помощью которого доказывают многие теоремы арифметики, алгебры, теории чисел и геометрии. Под индукцией (от латинского inductio — наведение) понимают в логике одну из форм умозаключений, состоящую в выведении общего суждения относительно бесконечного множества объектов на основании изучения некоторого конечного числа частных случаев.
Возникновение и применение идеи бесконечности в древнегреческой математике
Идея бесконечности возникла еще в глубокой древности в связи с представлениями о Вселенной. В философии под бесконечностью понимают отсутствие начала и конца во времени и в пространстве. Конечное и бесконечное — это две категории, т. е. два основных понятия, выражающие неразрывно связанные между собой противоположные стороны объективного мира. Вселенная, природа бесконечны. Бесконечная движущаяся материя существует в виде бесконечного многообразия взаимосвязанных конечных вещей. С понятием бесконечности в философии связано и математическое понятие бесконечности как одной из математических абстракций. Оно встречается уже на первых ступенях изучения арифметики, а именно когда речь идет о натуральном ряде чисел: 1, 2, 3, 4, .... В геометрии мы сталкиваемся с понятием бесконечности, когда прямая мыслится как бесконечная прямая и т. п.
Как известно, математика превратилась в дедуктивную науку в Древней Греции, где ее развитие протекало в сотрудничестве с философией. Уже в VI в. до н. э. греческие философы разрабатывали проблему бесконечности и связанную с ней проблему непрерывного и дискретного. Этими проблемами занимались представители милетской школы Анаксимандр (около 610—546 гг. до н. э.) в своем произведении «Апейрон» («Беспредельное»), Анаксимен (около 588гг. до н. э.) в сочинении «О природе». Такое же заглавие выбрал для одного из своих сочинений Анаксагор (около 500—428 гг. до н. э.), в котором он понятие бесконечности положил в основу своего мировоззрения. Анаксагор писал: «Среди малых величин не существует наименьшей, но уменьшение идет непрерывно». Эту мысль он дополнил, написав, что «всегда имеется нечто большее, чем то, что большое». Вот почему историки математики считают, что Анаксагор впервые ввел в математику понятие потенциально бесконечно малого и бесконечно большого, а это оказалось весьма существенным для дальнейшего развития математики. Но если Анаксагор и другие математики приписывали пространству только непрерывные свойства, то другие ученые создали представление о пространстве как о множестве точек, являющихся неделимыми элементами. Последняя концепция отвечала, в частности, духу школы Пифагора, в которой развивалось учение о дискретных (т. е. прерывных) объектах, а именно о числах. Пифагорейцы долгое время считали возможным распространить свое учение о целочисленной основе всего существующего и на геометрические величины. Открытие несоизмеримости, которое явно показало различие между дискретной природой (рациональных) чисел и непрерывной природой геометрических величин, привело, как известно, к большим трудностям, связанным с понятием бесконечности, к настоящему кризису в обосновании математики.
С точки зрения диалектического материализма в объективном реальном мире дискретное и непрерывное, движение и покой находятся в диалектическом единстве. Но нельзя отобразить движение, не остановив его, т.е. не прибегая к покою — его противоположности.
В настоящее время в основе изучения геометрии и математического анализа лежит понятие о вещественном числе. Множество вещественных чисел, как и множество точек прямой, обладает свойством непрерывности. Вещественным числом можно выразить отношение двух любых однородных величин. Однако, как известно, расширение понятия числа до вещественного и обоснование соответствующей теории были завершены только в XIX в.. Греки же, которые при открытии несоизмеримости имели представление лишь о дискретном множестве чисел (натуральных и в лучшем случае положительных рациональных), пошли в V—VI вв. по пути геометризации арифметики и строили общую теорию отношений, аналогичную нашей теории вещественных чисел, применяя ее к учению о подобии, к вопросам измерения площадей и объемов и вообще к исследованию непрерывных величин.
Изложим вкратце суть евдоксовой общей теории отношений (величин), содержащейся в V книге «Начал» Евклида (конец IV – III в. до н. э.). Величины здесь изображены отрезками, причем предполагается, что для любой пары величин найдется соответствующая пара отрезков а, b так, что отношение величин будет равно отношению отрезков а:b. В самом начале V книги вводится так называемая аксиома Архимеда, которую правильнее было бы называть аксиомой Евдокса (около 408 - около 355 до н. э.), или аксиомой Евдокса — Архимеда. Две однородные величины могут находиться в математическом отношении, только если на них распространяется эта аксиома которая является одной из аксиом непрерывности.
Равенство отношений определяется следующим образом: величины А, В имеют то же отношение, что и величины С, D, если для любой пары натуральных чисел тип выполняется какое-либо из следующих трех условий:
1) тА<пВ и тС<пD;
2) тА = пВ и тС = пD;
3) тА>пВ и тC>пD.
Современной операции умножения вещественных чисел у Евдокса соответствует составление отношений. «Составить» пару отношений А:В и В:С — значит найти отношение А:С, «составленное». Чтобы составить произвольные два отношения а:b и с:d, требуется предварительно найти отношение b:x, равное с:d, что осуществляется путем построения к любым трем отрезкам с, d, b четвертого пропорционального отрезка x. В V книге устанавливаются основные свойства отношений и их составления. Вышеприведенное определение отношений было, вероятно, подсказано Евдоксу как свойствами отношений соизмеримых величин, так и рассмотрением процесса измерения непрерывных геометрических величин. Целесообразность этого определения, конечно, можно проверить на разных примерах. О том, что некоторые математики неправильно его понимали, свидетельствует случай с французским ученым XVI в. П. Рамусом. Последний, возражавший против определения равенства отношений Евдокса, ссылался на следующий пример. Для чисел 4; 3 и 5; 4, т=6, п=9 имеет место неравенство
6·4<9·3 и 6·5<9·4,
но вместе с этим отношение 4:3 не равно отношению 5:4. Рамус не учел, что речь идет не об определенной одной паре или о конечном числе пар натуральных чисел т, п, а о произвольной паре. Достаточно в данном случае взять т=6, п=8, чтобы получить:
6·4=8·3,
в то время как 6·5<8·4.
Именно тот факт, что равенство отношений определяется Евдоксом с помощью бесконечного множества неравенств типа 1) или 3), вызывал много трудностей для понимания его теории, предвосхитившей теорию вещественных чисел Дедекинда (1831-1916). И метод исчерпывания Евдокса основывается на идее неограниченного приближения к некоторой величине с помощью последовательности неограниченного числа значений других величин и на основе безграничного деления любой величины на части, меньшие любых наперед заданных величин, т. е. в конечном итоге на идее потенциальной бесконечности, на которой базируется и метод пределов, которым пользуемся и мы. С помощью метода исчерпывания Евдокс строго доказал, что объем пирамиды равен 1/3 объема призмы с тем же основанием и высотой и другие предложения.
Понятие бесконечности развивалось в математике в тесной связи с решением конкретных математических задач и соответствующей разработкой математических методов (общая теория отношений, квадратура круга, метод исчерпывания и др.).
Широко использовал бесконечность в своих исследованиях и Архимед.
§1.2. История развития понятия функции.
Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.
Пропедевтический период (с древнейших времен до 17 века).
Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых, математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4-5 тыс. лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r2. Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции - теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости.
Введение понятия функции через механическое и геометрическое представления (17 век.)
Начиная лишь с 17 века, в связи с проникновением в математику идеи переменных, понятие функции применяется явно и вполне сознательно.
Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет (1540-1603) и Рене Декарт (1596-1650); они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы.
Кроме того, у Декарта и Ферма (1601-1665) в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы; он систематически рассматривал лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы. В 1671 году Ньютон (1643-1727) под функцией стал понимать переменную величину, которая изменяется с течением времени (называл в «флюентой»).
В «Геометрии» Декарта и работах Ферма, Ньютона и
Лейбница (1646-1716) понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями: ординаты точек кривых - функция от абсцисс (x); путь и скорость - функция от времени (t) и т.п.
Аналитическое определение функции (17 - начало 19 века).
Само слово «функция» (от латинского functio - совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673г. в письме к Гюйгенсу (1629-1695) (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати ввел с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа». В 18 веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Это так называемая аналитическая точка зрения на понятие функции. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли (1667-1748), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способ из этой переменной величины и постоянных». Для обозначения произвольной функции от x Бернулли применил знак j(x), называя характеристикой функции, а также буквы x или e ; Лейбниц употреблял x1, x2 вместо современных f1(x) , f2(x). Эйлер обозначил через f:x, f:(x+y) то, что мы ныне обозначаем через f(x), f(x+y).
Наряду с e Эйлер предлагает использовать буквы F,Y и другие. Даламбер сделал шаг вперед на пути к современным обозначениям, отбрасывая двоеточие Эйлера; он пишет, например, jt, j(t+s).
Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер (во «Введении в анализ бесконечного»): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего 18 века Даламбер, Лагранж (1736-1813), Фурье (1768-1830) и другие видные математики. Что касается Эйлера, то он не всегда придерживался выше указанного определения; в его работах понятие функции подвергалось дальнейшему развитию в соответствии с запросами математического анализа.
В «Дифференциальном исчислении», вышедшем в свет в 1755 году, Эйлер дает общее определение функции: «Когда некоторые количества зависят друг от друга таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функцией вторых». «Это наименование, - продолжает далее Эйлер - имеет чрезвычайно широкий характер; оно охватывает все способы, какими одно количество определяется с помощью других».
Как видно из определенных определений, само понятие функции фактически отождествлялось с аналитическим выражением. Новые шаги в развитии естествознания и математики вызвали и дальнейшее обобщение понятия функции.
Одним из нерешенных вопросов, связанных с понятием функции, по поводу которого велась ожесточенная борьба мнений, был следующий: можно ли одну функцию задать несколькими аналитическими выражениями?
Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых 18 века по поводу того, что стоит понимать под функцией, внес французский математик Жан Батист Жозеф Фурье, занимавшийся в основном математической физикой. В представляемых им в Парижскую АН в 1807-1811 гг. Мемуарах по теории распространения тепла в твердом теле, Фурье привел и первые примеры функций, которые заданы на различных участках различными аналитическими выражениями.
Из трудов Фурье следовало, что любая кривая независимо от того, из скольких и каких разнородных частей она состоит, может быть представлена в виде единого аналитического выражения и что имеются также прерывные кривые, изображаемые аналитическим выражением. В своем «Курсе алгебраического анализа», опубликованном в 1721г., французский математик О. Коши (1789-1857) обосновал выводы Фурье. Таким образом, на известном этапе развития физики и математики стало ясно, что приходится пользоваться и такими функциями, для определения которых очень сложно или даже невозможно ограничиться одним лишь аналитическим аппаратом. Последний стал тормозить требуемое математикой и естествознанием расширение понятия функции.
Идея соответствия (19 век).
В 1855 году Н.И. Лобачевский (1792-1856), развивая вышеупомянутое эйлеровское определение функции в 1755г., писал: «Общее понятие требует, чтобы функцией от x называть число, которое дается для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано и аналитическим выражением, или условием, которое подает средство испытывать все числа и выбирать одно из них; или, наконец, зависимость может существовать, или оставаться неизвестной... Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа, одни с другими в связи, принимать как бы данными вместе».
Еще до Лобачевского аналогичная точка зрения на понятие функции была высказана чешским математиком Б. Больцано (1781-1848).
Таким образом, современное определение функции, свободное от упоминании об аналитическом задании, обычно приписываемое немецкому математику П.Л. Дирихле (1805-1859), неоднократно предлагалось и до него. В 1837 году Дирихле так сформулировал общее определение понятия функции: «y есть функция переменной x (на отрезке a£x£b), если каждому значению x на этом отрезке соответствует совершенно определенное значение y, причем безразлично каким образом установлено это соответствие - аналитической формулой, графиком, таблицей либо даже просто словами».
Примером, соответствующим этому общему определению, может служить так называемая «функция Дирихле» j(x):

Эта функция задана двумя формулами и словесно. Она играет известную роль в анализе. Аналитически ее можно определить лишь с помощью довольно сложной формулы, не способствующей успешному изучению ее свойств. Таким образом, примерно в середине 19 века после длительной борьбы мнений понятие функции освободилось от рамок аналитического выражения, от единовластия аналитической формулы. Главный упор в основном общем определении понятия функции делается на идею соответствия.
Во второй половине 19 века после создания теории множеств в понятие функции, помимо идеи соответствия была включена и идея множества.
Таким образом, в полном своем объеме общее определение понятия функции формулируется следующим образом: если каждому элементу x множества А поставлен в соответствие некоторый определенный элемент y из множества В, то говорят, что на множестве А задана функция y=f(x), или что множество А отображено на множество В. В первом случае элементы x множества А называют значениями аргумента, а элементы их множества В - значениями функции; во втором случае x - прообразы, y - образы. В современном смысле рассматривают функции, определенные для множества значений x, которые возможно, и не заполняют отрезка a£ x£b, о котором говорится в определении Дирихле.
Достаточно указать, например, на функцию-факториал y=n!, заданную на множестве натуральных чисел. Общее понятие функции применимо, конечно, не только к величинам и числам, но и к другим математическим объектам. Например, к геометрическим фигурам.
При любом геометрическом преобразовании мы имеем дело с функцией. Другими синонимами термина «функция» в различных отделах математики являются: соответствие, отображение, оператор, функционал и др.Дальнейшее развитие математической науки в 19 веке основывалось на общем определении функции Дирихле, ставшим классическим.
Дальнейшее развитие понятия функции (20 век - ...).
Уже с самого начала 20 века определение Дирихле стало вызывать некоторые сомнения среди части математиков. Еще важнее была критика физиков, натолкнувшихся на явления, которые потребовали более широкого взгляда на физику. Необходимость дальнейшего расширения понятия функции стала особенно острой после выхода в свет в 1930 году книги «Основы квантовой механики» Поля Дирака (1902-1984), крупнейшего английского физика, одного из основателей квантовой механики. Дирак ввел так называемую дельта-функцию, которая выходила далеко за рамки классического определения функции. В связи с этим советский математик Н.М. Гюнтер (1871-1941) и другие ученые опубликовали в 30-40 годах нашего столетия работы, в которых неизвестными являются не функции точки, а «функции области», что лучше соответствует физической сущности явлений. Так, например, температуру тела в точке практически определить нельзя, в то время как температура в некоторой области тела имеет конкретный физический смысл. В общем виде понятие обобщенной функции было введено французом Лораном Шварцем. В 1936 году, 28-летний советский математик и механик С.Л. Соболев (род. в 1908г.) первым рассмотрел частный случай обобщенной функции, включающей и дельта-функцию, и применил созданную теорию к решению ряда задач математической физики. Важный вклад в развитие теории обобщенной функции внести ученики и последователи Шварца - И.М. Гельфант, Г.Е. Шилов и др.
§ 1.3. Различные современные подходы к определению понятия «функция».
Понятие функции часто встречается в школьном курсе математики и хорошо знакомо учащимся. Тем не менее на приемных экзаменах в вузах поступающие допускают много ошибок при использовании этого понятия. Объясняется это различными причинами, но в первую очередь тем, что слово «функция» используется в математике в нескольких смыслах, а в школьных учебниках это обстоятельство не разъяснено. Поэтому мы прежде всего обратимся к определению функции и другим относящимся сюда понятиям и подробно остановимся на тех различных пониманиях слова «функция», которые встречаются в школьном курсе математики.
Самым общим (и, безусловно, основным) является в математике следующее определение понятия функции. Говорят, что определена некоторая функция, если, во-первых, задано некоторое множество, называемое областью определения функции, во-вторых, задано некоторое множество, называемое областью значений функции, и, в-третьих, указано определенное правило, с помощью которого каждому элементу, взятому из области определения, ставится в соответствие некоторый элемент из области значений.
Приведем несколько примеров, иллюстрирующих это общее определение.
Пример 1. Обозначим через А множество всех треугольников на плоскости, а через В — множество всех окружностей, взятых на этой же плоскости. Множество А будем считать областью определения, а множество В - областью значений (той функции, которую мы определяем). Наконец, каждому треугольнику поставим в соответствие окружность, вписанную в этот треугольник. Это есть вполне определенное правило, которое каждому элементу взятому из области определения (т. е. треугольнику), ставит в соответствие некоторый элемент из области значений (т. е. окружность).
Пример 2. Сохраним те же самые множества А и В, что и в
примере 1, т. е. по-прежнему будем считать областью определения множество всех треугольников на плоскости, а областью значений—множество всех окружностей. Далее, каждому треугольнику поставим в соответствие его описанную окружность. Мы получаем функцию с той же областью определения А и той же областью значений В. Но это уже другая функция, так как окружность сопоставляется треугольнику с помощью другого правила.
Пример 3. Обозначим через К множество всех кругов на плоскости, а через О — множество всех действительных чисел. Далее, выберем единицу измерения площадей и каждому элементу множества К, (т. е. кругу) поставим в соответствие число, равное площади этого круга. Мы получаем функцию с областью определения К и областью значений D.
Пример 4. Обозначим через N множество всех натуральных чисел, а через О—множество всех действительных чисел. Далее, выберем два действительных числа a1 и r и каждому натуральному числу п поставим в соответствие действительное число, равное п-му члену арифметической прогрессии с первым членом а, и разностью r (т. е. натуральному числу п поставим в соответствие действительное число a1+(n-1)r ). Мы получаем функцию с областью определения N и областью значений D.
Пример 5. Теперь мы примем и в качестве области определения, и в качестве области значений множество D всех действительных чисел. Далее, выберем два действительных числа a1 и r и каждому действительному числу х поставим в соответствие число а1+(х-1)r. Мы получаем функцию с областью определения D и областью значений D.
Заметим, что в примерах 4 и 5 одинакова область значений D и одинаково правило соответствия: формулы a1+(n-1)r и а1+(х-1)r показывают, что в обоих случаях надо над выбранным числом (n или х) проделать одни и те же действия, чтобы узнать, какое число поставлено ему в соответствие. Однако области определения этих двух функций различны, и потому мы имеем в примерах 4 и 5 разные функции. Таким образом, для задания функции мало указать правило соответствия, а надо еще обязательно указать область определения и область значений.
Для обозначения функций обычно пользуются буквами. Одна буква (чаще всего х) используется для обозначения произвольного элемента, взятого из области определения функции. Эта буква называется аргументом. Таким образом, если сказано, что х - аргумент некоторой функции, то вместо х мы можем подставить любой элемент, принадлежащий области определения этой функции. Далее, другая буква (чаще всего у) используется для обозначения произвольного элемента, взятого из области значений. Эта буква называется функцией (и это второе значение слова «функция»). Наконец, третья буква (чаще всего f) используется для обозначения правила соответствия. Это значит, что если а - произвольное значение аргумента (т. е. произвольный элемент, взятый из области определения функции), то элемент, поставленный ему в соответствие, обозначается через f(а). Элемент y = f(а) называется значением рассматриваемой функции при х=а.
Все три буквы х, у, f объединяются одной записью:
y=f(x) (1)
(«игрек равен эф от икс»), которая и означает, что х - аргумент,
у - функция, а f - правило соответствия. Иногда букву f или выражение f(х) также называют функцией (и это - уже третье значение слова «функция»).
Пример 6. Обратимся снова к функции, рассмотренной в примере 4. Аргумент обозначим через п, функцию - через у, а правило соответствия - через f. Таким образом, мы запишем эту функцию в виде у=f(n). Вот несколько значений этой функции:
f(1)=a1, f(2)=a2=a1+r, f(3)=a3=a1+2r и т. д.
Разумеется, вместо букв х, у, f можно использовать и другие буквы. Например, запись s=j(t) означает, что s есть функция аргумента t (или короче: s есть функция от t), причем правило соответствия обозначается буквой j.
Следует подчеркнуть, что область значений функции представляет собой множество элементов (или чисел), среди которых обязательно содержатся все значения рассматриваемой функции. Однако в области значений могут содержаться и «лишние» элементы, не являющиеся значениями функции. Иными словами, множество значений функции обязательно содержится в области значений, но не обязательно совпадает с ней. Так, в примере 3 значениями функции являются лишь положительные числа, тогда как область значений есть множество всех действительных чисел. Несовпадение множества значений функции и области значений можно видеть также в примере 4.
В заключение рассмотрим еще одно (четвертое!) понимание слово «функция», являющееся для школьного курса математики наиболее важным. Именно, функцией называют произвольное выражение, содержащее аргумент х, а также знаки действий и числа. Например, функциями (в этом смысле) являются
y=x2+1, (2)
y=

y=|x-1|, (4)
y=
y=
y=
Почему же такие формулы называют «функциями» и не противоречит ли это понимание функции сказанному выше? Связь со сказанным выше устанавливается следующим соглашением, которого мы всюду в дальнейшем будем придерживаться:
Если функция задана в виде равенства, в левой части которого стоит у (или другая буква, обозначающая функцию), а в правой части стоит некоторое выражение, содержащее аргумент х, а также знаки действия и числа (причем область определения не указана), то принято считать, что
1) за область значений принимается все множество D действительных чисел;
2) за область определения принимается множество всех тех действительных чисел, при подстановке которых вместо х выполнимы (в множестве действительных чисел) все действия, указанные в правой части;
3) если число а принадлежит области определения, то значение функции при х=а равно числу, получающемуся, если в правую часть подставить х=а и произвести указанные действия.
Итак, задание функции формулой содержит в себе и указание области определения, и задание правила соответствия.
Пример 7. Найти область определения функций (2) и (3); определить, совпадают ли эти функции.
Решение. Действия, указанные в правой части равенства (2), выполнимы при любом действительном значении х, т. е. областью определения функции (2) является все множество D действительных чисел (или, иначе, бесконечный интервал -¥<х<¥). Функция (3) определена для всех действительных чисел х, кроме х=0, т. е. область определения этой функции получается выбрасыванием (или, как еще говорят, «выкалыванием») из множества D точки х=0. Можно описать область определения функции (3) и иначе: она представляет собой объединение двух бесконечных интервалов (-¥, 0) и (0, ¥).
Заметим, что при любом х¹0 значения функций (2) и (3) совпадают. Тем не менее (2) и (3)—различные функции, так как их области определения не совпадают.
Пример 8. Найти области определения функций (5),
Решение. Функция (5) определена для всех значений аргумента, кроме х=-2. Таким образом, область определения этой функции получается выкалыванием из числовой оси точки х=-2; иначе говоря, эта область определения является объединением двух бесконечных интервалов (-¥, -2) и (-2, ¥).
Область определения функции (6) состоит из всех точек, для которых подкоренное выражение неотрицательно, т.е. эта область определения задается неравенством 1+х³0, или х³-1. Иначе говоря, область определения функции (6) представляет собой бесконечный полуинтервал [-1,¥). Концевая точка х=-1 этого полуинтервала принадлежит области определения .
Наконец, область определения функции (7) состоит из всех значений х, для которых подкоренное выражение в правой части равенства (7) неотрицательно. Но если это подкоренное выражение отлично от нуля, то оно непременно отрицательно. Значит, область определения функции (7) состоит лишь из тех точек х, для которых подкоренное выражение обращается в нуль. Это будет при х=-5, х=-1 и х=2. Таким образом, область определения функции (7) состоит лишь из трех точек: -5, -1 и 2.
Пример 9. Найти область определения функции

Решение. Первое слагаемое f(х) определено при выполнении двух условий: 1) подкоренное выражение
0 1 2
0 1 2
Рис. 1.
неотрицательно, 2) знаменатель не обращается в нуль. Первое условие означает, что x³1 второе условие означает, что х¹2. Таким образом, область определения функции f(х) представляет собой объединение полуинтервала [1,2) и бесконечного интервала (2,¥). Далее, второе слагаемое g(x) определено при 5-x2³0, т.е. при -
Но для того, чтобы некоторая точка х=а принадлежала области определения функции у=f(х)+g(х), необходимо и достаточно, чтобы при х=а была определена и функция f(х), и функция g(х). Иными словами, область определения функции у=f(х)+g(х) представляет собой пересечение областей определения функций f(х) и g(х). Следовательно (рис. 1), область определения функции у=f(х)+g(х) представляет собой объединение полуинтервалов [1, 2) и (2,
§ 3.4. График функции.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х, а на оси ординат - значения функции у=f(х). Графиком функции у=f(х) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции y=f(x).
Другими словами, график функции у=f(х) - это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y=f(x).
| Рис. 3. |
 |

Рис. 2.
На рис. 2 и 3 приведены графики функций у=2x+1 и у=х2-2х.
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его куска, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х=а принадлежит области определения функции y=f(x), то для нахождения числа f(а) (т. е. значения функции в точке х=а) следует поступить так. Нужно через точку с абсциссой x=а провести прямую, параллельную оси ординат; эта прямая пересечет график функции у=f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 4). Например, для функции f(х)=х2-2х

Рис. 4.
с помощью графика (рис. 3) находим f(-1)=3, f(0)=0, f(1)=-1, f(2)=0 и т.д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 3 ясно, что функция y=х2-2х принимает положительные значения при х<0 и при x>2, отрицательные - при 0<х<2; наименьшее значение функция у=х2-2х принимает при х=1.
Для построения графика функции f(х) нужно найти все точки плоскости, координаты х, у которых удовлетворяют уравнению у=f(х). В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно - с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений - скажем, x1, х2, ..., хk - и составляют таблицу, в которую входят выбранные значения функции. Таблица выглядит следующим образом:
| x | x1 | x2 | … | xk |
| y | f(x1) | f(x2) | … | f(xk) |
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле, поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 10. Для построения графика функции y=f(х) некто составил таблицу значений аргумента и функции:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -1 | 0 | 1 | 2 | 3 |
 |
Соответствующие пять точек показаны на рис. 5. На основании расположения этих точек он сделал вывод,
Рис. 5.
что график функции представляет собой прямую (показанную на рис. 5 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. Простой пример иллюстрирует сказанное. Рассмотрим функцию
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 6). Другим примером может служить функция y=x+1+sinpx; ее значения тоже описываются приведенной выше таблицей.
| |
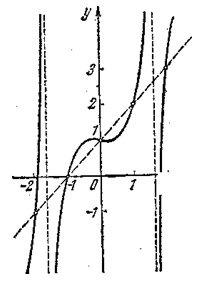 Этот пример показывает, что в «чистом» виде метод построения графика по нескольким точкам ненадежен.
Этот пример показывает, что в «чистом» виде метод построения графика по нескольким точкам ненадежен.
Рис. 6. |
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим в §4, а сейчас разберем некоторые часто применяемые способы построения графиков.
§ 1.5. Основные свойства функции п.1.5.1. ограниченность
Теперь мы должны ознакомиться со свойством функций, которое является интегральным, т. е. может быть определено сразу для любого множества значений независимой переменной, не нуждаясь в предварительном определении для отдельных её значений (в отдельных точках). Функция у=f(х) называется ограниченной на множестве M, если все значения, принимаемые ею на этом множестве, принадлежат некоторому отрезку; очевидно, вместо этого мы можем предъявить и совершенно равносильное требование: существует такое положительное число с, что f(х)<с для всех хÎМ. Более детально, мы называем функцию у ограниченной сверху (снизу) на М, если существует такое число с, что f(х)<с (f(х)>с) для всех хÎМ. Функция просто ограниченная должна быть для этого, очевидно, ограничена как сверху, так и снизу.
Число с, о котором говорится в определении ограниченности, выбирается сразу для всего множества М. В каждой отдельной точке этого множества, если функция в ней определена, такое число с существует тривиальным образом: для точки х достаточно положить, например, с=|f(x)|+1. Но функция, определённая, например, в каждой точке некоторого отрезка, может быть и неограниченной в этом отрезке; чтобы в этом убедиться, вспомним, что tgх возрастает безгранично при х®

не ограничена в отрезке [0,
Как для многих интегральных свойств, можно, однако, и для ограниченности функции на данном отрезке указать такое локальное свойство, выполнение которого в каждой точке данного отрезка равносильно выполнению рассматриваемого интегрального свойства. Условимся называть функцию у ограниченной в точке х, если она ограничена в некоторой окрестности U числа х. Мы можем теперь утверждать, что для ограниченности функции у=f(х) на отрезке [а, b] (закрытом) необходимо и достаточно, чтобы она была ограничена в каждой точке этого отрезка. Необходимость этого условия вытекает из самих определений и не нуждается в доказательстве; чтобы, показать его достаточность, допустим, что каждое число х отрезка [а, b] может быть окружено окрестностью Ux, в которой функция у ограничена: применяя лемму Гейне-Бореля, мы находим, что отрезок [а, b] покрывается конечным числом отрезков = D1, D2, ..., Dn) в каждом из которых у ограничена. Если |у|<Сi в отрезке Di (i=1, 2, ..., п) и если с есть наибольшее из чисел с1, с2, ..., сn, то |у|<с для всех хÎ[а, b], чем наше утверждение и доказано.
Условимся называть множество чисел N ограниченным, если все входящие в него числа могут быть заключены в некоторый отрезок. Очевидно, что ограниченность функции у=f(х) на множестве М равносильна ограниченности множества N значений, принимаемых этой функцией, когда величина х «пробегает» множество М, т. е. принимает всевозможные значения, принадлежащие этому множеству. Само собою ясно, что означают термины «множество N ограничено сверху (или справа)» и «множество N ограничено снизу (или слева)».
Условимся называть число b верхней гранью множества N, если: 1) множество N не содержит чисел, больших, чем b, и 2) в любой окрестности числа b найдётся число, принадлежащее этому множеству. Подобным же образом нижней гранью множества N мы назовём такое число a, что: 1) в множестве N нет чисел, меньших, чем a, и 2) в любой окрестности числа a найдётся число, принадлежащее множеству N. Очевидно, что множество, имеющее верхнюю (нижнюю) грань, ограничено сверху (снизу).
Пример 14. Доказать, что функция f(х)=
Решение. Нужно доказать, что для любого числа b существует (хотя бы одно) значение х из области определения функции, для которого f(x)
Область определения функции
п.1.4.2. четность, нечетность
Функция у=f(х) называется четной, если она обладает следующими двумя свойствами: 1) область определения этой функции симметрична относительно точки 0 (т.е. если точка а принадлежит области определения, то точка -а также принадлежит области определения); 2) для любого значения х, принадлежащего области определения этой функции, выполняется равенство f(x)=f(-x).
Функция у=f(х) называется нечетной, если:
1) область определения этой функции симметрична относительно точки 0;
2) 2) для любого значения х, принадлежащего области определения этой функции, выполняется равенство f(x)=-f(-x).
Без труда проверяется, что функция y=|х| является четной. Точно так же функция у=х2n четна, а функция у=x2n+1 нечетна (при любом целом п). Без труда проверяется также, что сумма, разность, произведение и частное двух четных функций снова являются четными функциями. Далее, сумма и разность двух нечетных функций являются нечетными функциями. Наконец, произведение и частное двух нечетных функций являются четными функциями, а произведение и частное четной и нечетной функций являются нечетными функциями
Из сказанного следует, например, что многочлен, у которого все показатели четны, является четной функцией, а многочлен, у которого все показатели нечетны, является нечетной функцией. Так, функция y=х4+2х2-1 четна, а функция х3-х5 нечетна.
Не следует думать, что всякая функция непременно является или четной или нечетной: существуют функции, не являющиеся ни четными, ни нечетными.
Пример 15. Доказать, что функция f(х)=2х+1 не является ни четной, ни нечетной.
Решение. Областью определения этой функции является вся числовая ось, т. е. условие 1) в определении четной и нечетной функций выполнено. Чтобы доказать, что функция f(х), не является четной, мы должны поэтому доказать, что условие 2) в определении четной функции не выполнено, т. е. что существует (хотя бы одно) значение х, для которого f(x)
Четность или нечетность функции весьма существенно сказывается на форме графика этой функции. Именно, имеют место следующие две теоремы:
Теорема. График четной функции симметричен относительно оси у.
| |
 Доказательство. Пусть точка (x0; y0) принадлежит графику четной функции у=f(х), т.е. у0=f(х0). Точка, симметричная с точкой у=f(х) относительно оси у, имеет координаты (-х0; у0). Надо доказать, что точка (-x0; y0) принадлежит графику функции у=f(х), т.е. доказать, что y0 =f(-х0). Но это следует из определения четной функции: f(-х0)=f(х0)=y0.
Доказательство. Пусть точка (x0; y0) принадлежит графику четной функции у=f(х), т.е. у0=f(х0). Точка, симметричная с точкой у=f(х) относительно оси у, имеет координаты (-х0; у0). Надо доказать, что точка (-x0; y0) принадлежит графику функции у=f(х), т.е. доказать, что y0 =f(-х0). Но это следует из определения четной функции: f(-х0)=f(х0)=y0. Рис. 10 |
 Теорема. График нечетной функции симметричен относительно начала координат (0; 0).
Теорема. График нечетной функции симметричен относительно начала координат (0; 0). Замечание. Из этих теорем следует, что для построения графика четной функции достаточно построить часть графика этой функции для х³0, а затем построенную часть графика симметрично отразить относительно оси у, т.е. для каждой точки графика с абсциссой х>0 построить точку, симметричную ей относительно оси у. В частности, таким способом можно построить график функции y=f(|x|), так как функция f(|x|) является четной. Для построения графика нечетной функции достаточно построить часть графика этой функции для х³0, а затем построенную часть графика симметрично отразить относительно точки (0; 0), т.е. для каждой точки графика с абсциссой х>0 построить точку, симметричную ей относительно начала координат. (Заметим, что для осуществления симметрии некоторой кривой относительно начала координат можно поступить следующим образом: сначала данную кривую К симметрично отразить относительно оси ординат, а затем полученную кривую К' симметрично отразить относительно оси абсцисс, рис. 10)
п.1.4.3. монотонность
Функция у=f(х) называется неубывающей на отрезке [а, b], если при а£х1£х2£b всегда f(x1)£f(x2); если при том же условии всегда f(x1)³f(x2), функция f(х) называется невозрастающей на отрезке [а,b]. Неубывающие и невозрастающие функции вместе образуют класс монотонных функций. Монотонные функции обладают целым рядом специальных свойств, которые делают их во многих случаях очень удобным орудием исследования.
Прежде всего всякая функция f(х), монотонная на данном, отрезке [а, b], ограничена на этом отрезке [как обычно, отрезок предполагается закрытым; для открытых отрезков утверждение неверно: функция у=
п.1.4.4. точки экстремума
Рассмотрим график непрерывной функции y=f(x), изображенной на рисунке. Значение функции в точке x1 будет больше значений функции во всех соседних точках как слева, так и справа от x1. В этом случае говорят, что функция имеет в точке x1 максимум. В точке x3 функция, очевидно, также имеет максимум. Если рассмотреть точку x2, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x2 минимум. Аналогично для точки x4.
Функция y=f(x) в точке x0 имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x0, т.е. если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)<f(x0).
Функция y=f(x) имеет минимум в точке x0, если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)>f(x0).
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.
Отмети, что если функция имеет в точке максимум, то это не означает, что в этой точке функция имеет наибольшее значение во всей области определения. На рисунке, рассмотренном выше, функция в точке x1 имеет максимум, хотя есть точки, в которых значения функции больше, чем в точке x1. В частности, f(x1)<f(x4) т.е. минимум функции больше максимума. Из определения максимума следует только, что это самое большое значение функции в точках, достаточно близких к точке максимума.
Теорема. (Необходимое условие существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x=x0 экстремум, то ее производная в этой точке обращается в нуль.
Доказательство. Пусть для определенности в точке x0 функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x0+Δx)<f(x0), т.е. f(x0+Dx)-f(x0)<0. Но тогда
Переходя в этих неравенствах к пределу при Δx→0 и учитывая, что производная f '(x0) существует, а следовательно предел, стоящий слева, не зависит от того как Δx→0, получаем: при Δx→0–0 f '(x0)≥0 а при Δx→0+0
f '(x0)≤0. Так как f '(x0) определяет число, то эти два неравенства совместны только в том случае, когда f '(x0)=0.
| Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль. Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную Функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует. Однако, если в некоторой точке x0 мы знаем, что f '(x0)=0, то отсюда нельзя делать вывод, что в точке x0 функция имеет экстремум. Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками. |
Теорема. (Достаточное условие существования экстремума.) Пусть функция непрерывна на некотором интервале, содержащем критическую точку x0, и дифференцируема во всех точках этого интервала (кроме самой точки x0). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x=x0 функция имеет максимум. Если же при переходе через x0 слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
Таким образом, если
a. f '(x)>0 при x<x0 и f '(x)<0 при x> x0, то x0 – точка максимума;
b. f '(x)<0 при x<x0 и f '(x)>0 при x> x0, то x0 – точка минимума.
Доказательство. Предположим сначала, что при переходе через x0 производная меняет знак с плюса на минус, т.е. при всех x, близких к точке x0 f '(x)>0 для x< x0, f '(x)<0 для x> x0. Применим теорему Лагранжа к разности f(x)-f(x0) = f '(c)(x-x0), где c лежит между x и x0.
1. Пусть x <x0. Тогда c<x0 и f '(c)>0. Поэтому f '(c)(x-x0)<0 и, следовательно,
f(x) - f(x0)<0,т.е. f(x)< f(x0).
2. Пусть x > x0. Тогда c> x0 и f '(c)<0. Значит f '(c)(x- x0)<0. Поэтому f(x) - f(x0)<0, т.е. f(x) < f(x0).
Таким образом, для всех значений x достаточно близких к x0 f(x)<f(x0). А это значит, что в точке x0 функция имеет максимум.
Аналогично доказывается вторая часть теоремы о минимуме.
Проиллюстрируем смысл этой теоремы на рисунке. Пусть
f '(x1)=0 и для любых x, достаточно близких к x1, выполняются неравенства
f '(x)<0 при x< x1, f '(x)>0 при x> x1.
Тогда слева от точки x1 функция возрастает, а справа убывает, следовательно, при x=x1 функция переходит от возрастания к убыванию, то есть имеет максимум.
Аналогично можно рассматривать точки x2 и x3.
Правило исследования функции y=f(x) на экстремум
1. Найти область определения функции f(x).
2. Найти первую производную функции f '(x).
3. Определить критические точки, для этого:
a. найти действительные корни уравнения f '(x)=0;
b. найти все значения x при которых производная f '(x) не существует.
4. Определить знак производной слева и справа от критической точки. Так как знак производной остается постоянным между двумя критическими точками, то достаточно определить знак производной в какой-либо одной точке слева и в одной точке справа от критической точки.
5. Вычислить значение функции в точках экстремума.
Наибольшее и наименьшее значения функции на отрезке.
Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.
Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.
Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:
1. Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.
2. Вычислить значения функции на концах отрезка при x=a, x=b.
3. Из всех полученных значений выбрать наибольшее и наименьшее.
п.1.4.5. непрерывность
Приступая к изучению функциональных зависимостей, мы должны, конечно, прежде всего с помощью целесообразной классификации внести хотя бы некоторый порядок в предстоящий нам многообразный мир. Первым таким классифицирующим и организующим принципом служит обычно (и с полным основанием) разделение всех функций на непрерывные и разрывные, причём математический анализ фактически имеет дело почти исключительно с непрерывными функциями, лишь в сравнительно редких случаях привлекая к рассмотрению и простейшие из разрывных. Непрерывные функции обладают целым рядом особых свойств, которых лишены, вообще говоря, функции разрывные; благодаря этим свойствам исследование и применение непрерывных функций весьма значительно облегчаются, так что изучение этих свойств становится для анализа чрезвычайно важным делом.
Мы говорим, что функция у=f(х) непрерывна при х=а (или, короче, в точке а), если

По поводу этого определения надо прежде всего заметить, что так понимаемая непрерывность есть локальное (местное) свойство функции, т. е. такое свойство, которым функция может обладать в одной точке и не обладать в другой; так, функция (3) разрывна (т. е. не непрерывна) при х=0 и непрерывна при любом другом значении х; это - очень важное обстоятельство, которое никогда не надо упускать из вида.
Далее, мы называем, функцию непрерывной в данном отрезке [а,b], если она в вышеприведённом смысле непрерывна в каждой точке этого отрезка; при этом в точке а требуется лишь непрерывность справа, т, е. соотношение
с помощью которого определение непрерывности функции f(x) в точке а можно записать посредством весьма простого соотношения
f(a+0)=f(a-0)=f(a);
это обозначение не может привести ни к каким смешениям, если только помнить, что f(а+0) и f(а-0) представляют собой не значения функции f(х) в каких-либо точках, а пределы таких значений при некоторых определённых изменениях величины х.
п.1.4.6. периодичность
Функция у=f(х) называется периодической, если существует такое число Т>0, что для, каждого значения х из области определения этой функции значения х+Т и х-Т также принадлежат области определения и выполняется равенство f(x+Т)=f(x). При этом число Т называется периодом функции y=f(x). Из этого определения следует, что
f(х+2T)=f[(x+T)+T]=f(x+T)=f(x),
f(х+3T)=f[(x+2T)+T]=f(x+2T)=f(x),
f(x)=f[(x-T)+T]=f(x-T)
и т. д. Отсюда, используя метод математической индукции,

Рис. 12
получаем, что для любого п = 0, ±1, ±2, …, выполняется равенство f(х+пТ)=f(х), Таким образом, каждое из чисел nТ (п=1,2,3,…) также является периодом функции f(х).
Мы предполагаем, что читатель хорошо знаком с периодическими функциями sinx, соsx и tgх.
Пример 16. Доказать, что функция
Решение. Область определения рассматриваемой Функции получается выбрасыванием из числовой оси тех точек, в которых знаменатель обращается в нуль, т. е. точек -
f(x+2p)=

Пример 17. Доказать, что функция f(х)=|sinх| является периодической с периодом p.
Решение. Область определения функции f(х)=|sinх| вся числовая ось. Поэтому для любого k точки х+p и х-p принадлежат области определения. Остается проверить, что выполнено равенство f(х+p)=f(х). Мы имеем f(х+p)=|sin(x+p)|=|-sinx|=|sinx|=f(x).
Глава II. Изучение основных элементарных функций в школьном курсе математики.
В результате изучения курса математики учащиеся должны:
§ понимать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами, что конкретные типы функций (прямая и обратная пропорциональности, линейная, квадратичная функции) описывают большое разнообразие реальных зависимостей;
§ правильно употреблять функциональную терминологию (значение функции, аргумент, график функции, область определения, возрастание и др.), понимать ее в тексте, в речи учителя, в формулировке задач;
§ находить значения функции, заданных формулой, таблицей, графиком; решать обратную задачу;
§ находить по графику функции промежутки возрастания и убывания функции, промежутки знакопостоянства, наибольшее и наименьшее значения;
§ строить графики линейной функции, прямой и обратной пропорциональности, квадратичной функции;
§ интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы.
Школьный курс изучения функции строится по аналогии с развитием в истории понятия функции.
§2.1. Линейная функция.
Линейной функцией называется функция, которую можно задать формулой вида y=kx+b, где х – независимая переменная, k и b – некоторые числа. Такое определение дает Ю.Н. Макарычев и др. в своем учебнике по алгебре в 7 классе, в параграфе 13.
И только после этого в следующем параграфе дается определение прямой пропорциональности. Перед тем как ввести определение предлагается задача об объеме железного бруска. Зависимость массы железного бруска от его объема является примером функции, которая задается формулой вида у=kх. И только затем дается определение. Обращается внимание на то, что прямая пропорциональность является частным случаем линейной функции, так как формула у=kх получается из формулы y=kx+b при b=0 и для того, чтобы построить график прямой пропорциональности достаточно отметить какую-либо точку графика, отличную от начала координат, и провести через эту точку и начало координат прямую.
Целый параграф в данном учебнике отводится на изучение взаимного расположения графиков линейных функций. Графики двух линейных функций, заданных формулами вида y=kx+b, пересекаются, если коэффициенты при х различны, и параллельны, если коэффициенты при х одинаковы.
В отличие от учебника Ю.Н. Макарычева и др, в учебнике Ш. А. Алимова и др. понятие прямой пропорциональности вводится раньше линейной функции. Школьникам предлагается найти площадь треугольника, основание которого равно 3, а высота х. пусть искомая площадь будет у. Тогда ответ можно записать у=3х. если же основание треугольника равно k, тогда зависимость между высотой х и площадью у выражается формулой у=kх. Все первоначальные сведения о линейной функции вводятся на примере его частного случая у=kх. В отличии от Ю.Н. Макарычева и др, школьников уже в 7 классе знакомят с понятием обратной пропорциональности. Как пример приводится зависимость скорости от времени. Говорится о том, что плотность вещества при постоянной массе обратно пропорциональна его объему.
И только в следующем параграфе дается определение линейной функции в общем виде. Школьникам объясняется, что график функции y=kx+b получается сдвигом графика функции y=kx на b единиц вдоль оси ординат. Графики данных функций параллельны.
В учебнике А.Г. Мордковича понятие «Линейная функция» вводится совсем иначе. Поскольку определение функции будет дано только в 9 классе, изменяется традиционная методика изложения темы «Линейная функция» - первой темы, связанной с понятием функции. Первой (в §28) изучается тема «Линейные уравнения с двумя переменными». Рассматриваются задания следующего типа:
- найти какое либо решение уравнения 2х+3у=5;
- найти решение уравнения 2х+3у=5, зная, что х=2, зная что у=0, и т.п.;
- построить график уравнения х+у=3 и с помощью графика узнать несколько решений этого уравнения.
Далее внимание учащихся обращается на то, что график линейного уравнения с двумя переменными с двумя переменными проще строить, если уравнение преобразовано к виду y=kx+b, для которого употребляется термин «линейная функция». Позднее им сообщается, что существуют и другие функции, например у=х2 (ее изучению посвящена глава 7).
В учебнике вводятся теоремы без доказательства, например:
Теорема 2. Графиком линейной функции y=kx+b является прямая.
Теорема 4. Прямая, служащая графиком линейной функции y=kx+b, параллельна прямой, служащей графиком прямой пропорциональности y=kx.
§2.2. Квадратичная функция.
С квадратичной функцией учащиеся в учебниках Ш.А. Алимова впервые сталкиваются в 8 классе.
В §35 учащиеся знакомятся с определением квадратичной функции. Даются примеры из жизни, где имеет место быть квадратичная функция. Например, зависимость площади квадрата от его стороны является примером функции y=x2.
В §36 предлагается рассмотреть функцию y=x2, т.е. квадратичную функцию y=ax2+bx+c при, а=1, b=0, с=0.
Для построения функции составляется таблица, а затем точки отмечаются на координатной плоскости и соединяются. График функции y=x2 называется параболой.
После чего выясняются некоторые свойства функции y=x2.
В §37 учащимся предлагается построить график функции y=ax2. Сравнивается графики функций y=ax2 и y=x2. Говорят, что график функции y=аx2 получается растяжением графика функции y=x2 от оси Ох вдоль оси Оу в а раз.
Рассматриваются свойства функции y=ax2, где а¹0
1) если а>0, то функция y=ax2 принимает положительные значения при х¹0;
если а<0, то функция y=ax2 принимает отрицательные значения при х¹0;
2) Парабола y=ax2 симметрична относительно оси ординат;
3) Если а>0, то функция y=ax2 возрастает при х³0 убывает и при х£0;
Если а<0, то функция y=ax2 убывает при х³0 и возрастает при х£0.
В §38 автор предлагает построить график квадратичной функции. Для этого предлагается использовать метод выделения полного квадрата (получили у=(х+т)2+п), а затем сравнить полученный график с графиком функции у=х2. Делается вывод что мы получаем параболу сдвинутую на т единиц по оси Ох и на п единиц по оси Оу.
В §39 приводится алгоритм построения графика любой квадратичной функции y=ax2+bx+c:
1. Построить вершину параболы (х0, у0), вычислив х0, у0 по формулам
2. Провести через вершину параболы прямую параллельную оси ординат, - ось симметрии параболы.
3. Найти нули функции, если они есть, и построить на оси абсцисс соответствующие точки параболы.
4. Построить две какие-то точки параболы, симметричные относительно ее оси. Для этого надо взять две точки на оси, симметричные относительно точки х0 (х0 ¹ 0), и вычислить соответствующие значения функции (эти значения одинаковы). Например, можно построить точки параболы с абсциссами х=0 и х=2х0 (ординаты этих точек равны с)
5. Провести через построенные точки параболу.
При изучении темы формируются умения определять по графику промежутки возрастания функции, промежутки знакопостоянства, нули функции. Нахождение наибольшего и наименьшего значений функции и решение задач с их применением не входит в число обязательных.
В заключении, учащимся предоставляется возможность еще раз повторить решение систем двух уравнений, одно из которых первой, а другое второй степени.
В учебниках Ю.Н. Макарычева и др. с функцией y=x2 учащиеся впервые сталкиваются в 7 классе. Все сведения рассматриваются в этом параграфе аналогично учебнику Ш.А. Алимова за 8 класс.
Дальнейшее же знакомство с квадратичной функцией происходит только в 9 классе.
Квадратичной функцией называется функция, которую можно задать формулой вида y=ax2+bx+c, где х – независимая переменная, а, b и с – некоторые числа, причем, а¹0 - так начинается §3 в данном учебнике.
Изучение квадратичной функции начинают с частного случая – функции y=ax2.
При а=1 формула y=ax2 принимает вид y=x2. С этой формулой учащиеся уже встречались в 7 классе. В отличии от учебника Ш. А. Алимова формулируется 5 свойств. Добавляется свойство, что график функции проходит через начало координат, и свойство о наибольшем и наименьшем значении.
В следующем пункте рассматриваются графики функции у=ах2+п и у=а(х-т)2. Учащимся предлагается выяснить, что представляют собой графики данных функций.
И наконец в последнем пункте данной темы рассматривется построение графика квадратичной функции. Здесь предлагается алгоритм построения квадратичной функции, состоящий из трех пунктов:
1) Найти координаты вершины параболы и отметить ее в координатной плоскости;
2) Построить еще несколько точек, принадлежащих параболе;
3) Соединить отмеченные точки плавной линией.
В учебнике Мордковича функция y=x2 вводится в седьмом классе:
во–первых, для того чтобы школьник, целый год изучавший курс алгебры, не закончил год с убеждением, что в природе существуют только линейные функции; надо приоткрыть двери в дальнейшие разделы математики;
во–вторых, эта функция помогает более глубокому изучению линейной функции.
В результате в 7 классе учащиеся знакомятся с графиком и свойствами функции y=x2, учатся графически решать уравнения.
Дальнейшее знакомство с данной функцией происходит в 8 классе. Так, в §12 приведены два алгоритма построения графика функции у=f(x+l)+m, если известен график функции y=f(x).
В §13, где идет речь о построении графика квадратичной функции, делается акцент не на отыскании координат вершины параболы, служащей графиком функции y=ax2+bx+c, а на отыскании уравнения оси симметрии параболы
§2.3. Обратная пропорциональность.
В учебниках Алимова функция у=
Во второй задаче предлагается построить график функции у=
В конце параграфа приводится пример из жизни, где встречается данная функция. Говорится, что функция у=
Например, при равномерном движении по окружности с постоянной скоростью v тело движется с центростремительным ускорением а, равным
Учащимся предстоит овладеть такими свойствами, как область определения, четность и нечетность функции, возрастание и убывание функции на промежутке.
В учебнике Макарычева данная функция вводится в 8 классе. На изучение данной функции отводится только § 8 из третьей главы. Параграф начинается с примера о площади прямоугольника, благодаря чему учащихся подводят к определению обратной пропорциональности. Далее приводится пример построения графика функции при k>0. Обращается внимание на то, что при х=0 выражение
В учебниках мордковича обратная функция изучается в 8 классе вместе с функцией y=x2. И вводится точно так же как в учебнике Макарычева.
§2.4. Степенная функция.
В учебниках Алимова со степенной функцией ученики встречаются в 9 классе.
С функциями у=х и у=х2 учащиеся познакомились, и им объясняется что эти функции – частный случай степенной функции у=хr, где r –заданное число (причем как целое, так и дробное). После чего формулируются свойства данной функции в зависимости r, которое может быть как положительным, так и отрицательным.
В учебниках Макарычева с функцией у=хr учащиеся сталкиваются тоже только в 9 классе, В §22 рассматривается только натуральный показатель. При формулировке свойств, берется два случая, когда показатель степени четный и когда нечетный.
С дробным показателем рассматривается единственная функция в 8 классе у=
В учебниках Мордковича функция у=
Знакомство же со степенной функцией происходит лишь в 11 классе. Первой функцией, с которой знакомятся учащиеся, становится
Точки М(а;ь) и Р(ь;а) симметричны относительно прямой у=х.
После чего идет доказательство теоремы..
Формулируются свойства функции
И наконец, §44 посвящен уже степенной функции вида у=хr, где r – любое действительное число. Основная цель этого параграфа – добиться того, чтобы учащиеся четко представляли себе эскиз графика степенной функции у=хr для любого рационального показателя r и знали свойства степенной функции.
При формулировке свойств рассматривается три случая: степень больше единицы, степень больше нуля, но меньше единицы и отрицательная степень.
В этом же параграфе идет речь о дифференцировании и интегрировании степенной функции. Повторяется материал 10 класса: составление уравнения касательной, исследование функций на монотонность и экстремумы, построение графиков функций, отыскание наибольшего и наименьшего значений функции на промежутке с помощью производной, вычисление площади плоских фигур.
§2.5. Показательная функция.
В 10 классе в учебнике Алимова рассматривается показательная функция. Основная цель –познакомить с многообразием свойств и графиков показательной функции в зависимости от значений оснований и показателей степени.
Первое с чем знакомятся ученики на уроках математики – это свойства показательной функции и ее графиком. На ее изучение отводится один параграф, который начинается с повторения свойств степеней. После чего вводится определение показательной функции. Далее рассматриваются основные свойства показательной функции. Свойства монотонности обосновываются аналитически и иллюстрируются на графике. В дальнейшем основное внимание уделяется иллюстрации свойств функции по графику (чтение графика). Приводятся примеры применения показательной функции для описания различных физических процессов. В учебнике приводится в пример формула радиоактивного распада

В учебниках Колмогорова показательная функция изучается в 11 классе. Прежде чем ввести понятие показательной функции f(x)=ax, где х принимает любые значения из множества действительных чисел, проводится подготовительная работа. Начинается со знакомства учащихся с функцией f(x)=ax, область определения которой – множество рациональных чисел. Для каждого положительного числа а можно найти значение выражения
В учебнике Мордковича учащиеся впервые сталкиваются с понятием показательной функции уже в 9 классе, на примере формулы п-го члена геометрической прогрессии. Следующая встреча с данной функцией у учащихся происходит только в 11 классе. В §45 сначала рассматривается функция у=2х, хÎQ. При рассмотрении свойств у=2х отмечается, что это возрастающая функция, неограниченная сверху и ограниченная снизу, не имеющая ни наименьшего, ни наибольшего значения.
Кроме того, рассматривается функция у=2х при х=
При формулировке общих свойств графика функции, рассматриваются два случая, когда основание целое число и дробное число большее нуля, но меньшее единицы. И только после этого вводится определение показательной функции.
Кроме того, в учебнике Мордковича изучается горизонтальная асимптота графика функции, и способ ее отыскания.
В учебнике обращается внимание на то, что учащиеся иногда путают понятия показательной функции и стенной. Предлагается сравнить данные функции. Далее автор не забывает упомянуть функцию
Во втором замечании автор говорит, что не рассматривается показательная функция с основанием а=1.
§2.6. Логарифмическая функция.
В учебнике Алимова с логарифмической функцией учащиеся впервые сталкиваются в 10 классе.
Основная цель – познакомить учащихся с логарифмической функцией, ее свойствами и графиком.
До введения понятия логарифмической функции формируется понятие логарифма числа, изучаются свойства логарифмов.
§6 начинается с определения логарифмической функции. После чего формулируются свойства данной функции. Аналитическое обоснование свойств функции от всех учащихся не требуется.
В конце параграфа дается теорема:
если logax1=logax2, где a>0, a¹1, x1>0, x2>0 то x1=x2.
В учебнике Колмогорова логарифмическая функция вводится 11 классе. Логарифмическая функция, как и показательная, не может впервые вводится с помощью формулы (как это делается в учебнике Алимова). Причина этого в том, что в курсе алгебры еще не введено понятие логарифма числа. Поэтому функция вводит, как обратную к показательной функции f(x)=ax , хÎR. Основные свойства логарифмической функции вытекают из свойств показательной функции и теоремы об обратной функции. (Причем у Алимова понятие обратной функции вводится после введения логарифмической функции.) В отличии от учебника Алимова у Колмогорова не сформулировано свойство о положительных и отрицательных значениях х.
В учебнике Мордковича понятие логарифма в §48 вводится при помощи графических соображений. Предлагается одновременно рассмотреть две функции
При формулировке свойств рассматривается два случая, когда основание больше 1 и когда основание больше нуля, но меньше единицы. Кроме тех свойств, которые перечислены в учебниках Алимова и Мордковича здесь рассматриваются свойства выпуклости, непрерывности, ограниченности, четности, наибольшего или наименьшего занчения.
§2.7. Тригонометрические функции.
В 11 классе в учебнике Алимова изучаются свойства и графики функций y=cosx, y=sinx, y=tgx. Обратные тригонометрические функции.
Основная цель – изучить свойства тригонометрических функций, научить учащихся строить их графики.
Первой тригонометрической функцией, с которой знакомятся учащиеся, становится функция y=cosx, в §19.
Изучение данных функций начинается с повторения определения синуса, косинуса и тангенса произвольного угла которые были введены в 9 классе.
Так как функция y=cosx периодична с периодом 2p, то достаточно построить ее график на каком-нибудь промежутке длиной 2p. Кроме того достаточно построить ее график на отрезке 0£х£p, а затем симметрично отразить относительно оси Оу. Прежде чем перейти к построению графика, доказывается, что функция y=cosx убывает на отрезке 0£х£p. Доказанное здесь свойство позволяет сделать вывод о возможности построения графика функции на этом отрезке и распространении его на всю числовую прямую.
После построения формулируются основные свойства функции y=cosx.
В §20 вводится функция y=sinx. Для построения функции используют формулу:
Эта формула показывает, что график функции y=sinx можно получить сдвигом графика функции y=cosx вдоль оси абсцисс вправо на
Затем формулируются свойства функции y=sinx.
В §21 изучается функция y=tgx.
Построение графика функции тангенс, как и косинус, начинается с исследования. Сначала график строится на промежутке
После чего формулируются свойства функции y=tgx.
В учебнике Колмогорова все тригонометрические функции вводятся в одном параграфе, который начинается с основных тригонометрических определений. Данные определения не являются новыми для учеников - это повторение материала 9 класса. После этого происходит построение графика функции y=sinx по точкам с использованием свойств периодичности и единичной окружности.
По графику демонстрируются свойства данной функции: ее область определения, область значения, наибольшее и наименьшее значения, нули функции, промежутки постоянных знаков функции. Аналогично рассматриваются свойства функции y=cosx и y=tgx и на графиках этих функций демонстрируются их свойства.
В 9 классе в учебнике Мордковича предлагаются элементы теории тригонометрических функций. Эта глава рассматривается, как дополнительный материал. Весь этот материал повторен и расширен в курсе алгебры и начала анализа в 10-11 классе.
В начале 10 класса учащиеся подробно изучают данный материал. На изучение данного материала отводится 15 параграфов, а по времени – 18 часов.
В §1 и в §2 учащиеся знакомятся с числовой окружностью и с определением тригонометрических функций. Автор выделяет числовую окружность в качестве самостоятельного объекта изучения. Школьникам напоминается материал о вычислении длин дуг окружностей.
Числовая окружность на плоскости рассматривается в §3.
Для изучения числовой окружности автор предлагает игровые моменты.
Изучение самих функций начинается только с 9 параграфа. Перед этим вводятся определения синуса, косинуса , тангенса и котангенса. Первой функцией предлагается y=sinx. Параграф начинается с формулирования свойств функции. После чего предлагается построить график данной функции на отрезке [0; p]. Затем добавляют к построенному графику симметричную ему относительно начала координат линию. Получили график на отрезке [-p; p]. Далее предлагается построить график функции на отрезке [p; 3p]. В результате получили то же самое, что и на отрезке [-p; p].
В следующем параграфе предлагается к рассмотрению функцию y=cosx. Ее график получается из графика функции y=sinx сдвигом на
В §15 учащимся предлагается функция y=tgx и y=сtgx. Отмечаются их свойства. Графики строятся так же как в учебниках Алимова.
Глава III. Вспомогательные приемы построения усложненных графиков.
Известно, что методы высшей математики позволяют строить любой график. Однако знаний тех элементов высшей математики, которые даются в средней школе, для этой цели недостаточно. С другой стороны, большое количество графиков, иногда весьма интересных может быть построено средствами исключительно элементарной математики. Наиболее трудные из этих графиков требуют для своего построения хорошего знания многих разделов элементарной математики, а подчас и остроумного применения этих знаний. Построение графиков средствами элементарной математики может служить материалом для закрепления и усовершенствования учениками и абитуриентами своих знаний по многим важным разделам элементарной математики.
§3.1. Параллельный перенос.
п 3.1.1 Сдвиг оси х-ов.
Разобьем этот прием на примере построения графика функции
График этой функции можно построить, пользуясь общими приемами:
1) область существования: (-¥;¥), т.е. вся числовая ось;
2) область изменения функции – полуоткрытый интервал 1£у<¥;
3) функция четная;
4) при х=0 у=1, т.е. кривая пересекает ось у-ов в точке (0;1); в этой точке функция имеет минимум, так как х2 =0, откуда у³1;


Рис.13. Рис.14.
5) контрольная точка: при х=2 у=4+1=5; точка (2; 5).
По этим данным график функции построен на рис. 13.
Тот же график можно построить проще, воспользовавшись уже известным нам графиком функции у=х2. Для этого наносим штриховой линией график функции у=х2 (рис. 14), назовем его исходным графиком.
Сравнивая графики функций у=х2+1 и у=х2, видим, что ординаты у графика заданной функции на 1 больше ординат исходного графика. Следовательно, исходный график надо перенести на 1 вверх, как это и сделано на рисунке 14.
График функции у=х2+1 можно построить еще проще, если воспользоваться тем же исходным графиком (y=x2), но вместо перенесения всей кривой вверх на 1 перенести ось х-ов на ту же 1 вниз, как показано на рисунке 15. Тем самым относительно новой оси х-ов все ординаты
 |
|

кривой у=х2 увеличиваются на 1 и получается график заданной функции у=х2+1.
Следовательно, график функции y=f(x)+b, где f(x) - простейшая функция, график которой нам известен, можно построить следующим простейшим приемом (рис. 15).
Строится известный нам график функции у=f(х), причем горизонтальная ось вычерчивается штриховой линией. Затем она сдвигается на (-b). Это и есть истинная ось х-ов; первоначальную же горизонтальную ось, нанесенную штриховой линией, можно стереть.
Например, для построения графика функции у=f(x)+3 горизонтальная штриховая ось графика функции у=f(x) сдвигается на 3 единицы вниз, т. е. на (-3); для построения графика функции y=f(x)-3 горизонтальная штриховая ось сдвигается на (+3), т. е. на 3 единицы вверх.
п 3.1.2. Сдвиг оси у-oв
Разберем этот прием на примере построения графика функции
y=(x+1)2.
Общий метод построения графика:
1) область существования — вся числовая ось;
2) область изменения функции - полуоткрытый интервал 0£у<¥;
3) функция не обладает свойствами четности и нечетности;
4) при у=0 (х+1)2=0, или х+1=0, откуда х=-1, т. е. кривая пересекает ось х-ов в точке (-1; 0);
5) при х=0 у=1, т. е. кривая пересекает ось у-ов в точке (0; 1);
6) контрольные точки:
x=2; у=(2+1)2=9; точка (2; 9);
x=-3; у=(-3+1)2=4; точка (-3; 4).
 |
По этим данным график функции построен на рисунке 17.
 |
Другой способ построения графика функции у=(х+1)2 показан на рисунке 18.
Вначале строится (штриховой лини ей) график исходной функции y=х2.
Далее замечаем, что каждая ордината графика функции y=(х+1)2 равна той ординате исходного графика, которая соответствует абсциссе х+1, т.е. на 1 большей, нежели действительная абсцисса исходного графика.
Например, при х=1 у=(х+1)2=22=4, т. е. при х=1 надо отложить по оси у-ов не 12, а 22=4, т. е. (1+l)2. Эта ордината точки А исходного графика соответствует абсциссе х=2, а для графика заданной функции она соответствует абсциссе х=1, следовательно, точку А надо сдвинуть по оси х-ов на (-1), в точку А1. Таким же образом и в с е точки исходного графика должны быть сдвинуты по оси х-ов на (-1), т. е. весь график исходной функция должен быть сдвинут влево на 1, что сделано на рисунке 18.
Проще вместо перенесения всей кривой на 1 влево сдвинуть ось у-ов на 1 вправо, как это показано на рисунке 19.
Таким образом, график функции y=f(x+a), где f(x)- простейшая функция, график которой нам известен, строится так (рис. 20).
Наносится график функции у=f(x), причем вертикальная ось у-ов вычерчивается штриховой линией. Затем эта вертикальная ось сдвигается на (+а). Это и будет истинная ось у-ов; первоначальную вертикальную ось можно затем стереть.
 |

Рис 19 Рис 20
Например, для построения графика функции y=f(x+3) вертикальная ось графика функции f(x) сдвигается на 3 единицы вправо, т. е. на (+3); для построения графика функции y=f(x-3) вертикальная ось сдвигается на 3 единицы влево, т. е. на (-3).
Примечание. 1. Необходимо иметь в виду, что сдвиг оси у-ов надо производить на величину «добавка» к положительному значению аргумента х, так что если задана функция y = f(-х+а), то ее надо сначала преобразовать в функцию y=f[-(х-а)] и принять за исходную функцию
f(-х), а затем сдвинуть ось у-ов на (-а), т. е. на добавок к (+x).
Пример. у=(-х+1)2.
Преобразуем: у=[-(x-l)]2=(x-1)2.
Приняв за исходную функцию у=х2, как и при построении графика функции у=(х+1)2 (рис. 19), сдвигаем ось у-ов на (-1), т. е. на добавок к (+х) (рис. 21), а не на (+1), как на рисунке 19.
Для построения графика функции у=(-х+1)3 следует, преобразовав ее в функцию у=[-(х-1)]3, принять за исходный график заданной функции у=(-х)3=-х3 и сдвинуть ось у-ов на (-1).
Примечание 2. Если требуется построить график функции у=f(x+а)+b (рис. 22), то сначала строится график функции у=f(х), причем обе оси наносятся штриховыми линиями. Затем горизонтальная ось сдвигается на (-b), т.е. в сторону, обратную знаку добавка к функции, вертикальная ось сдвигается на (+а), т.е. в сторону знака добавка к аргументу.
Если имеется добавок только к функции или только к аргументу, то при построении исходного графика можно также обе оси координат нанести штриховыми линиями; затем одну из них сдвинуть, а другую обвести сплошной линией.


Рис. 21. Рис. 22.
§ 3.2. Растяжение и сжатие графика.
п.3.2.1. По оси х-ов.
Этот прием чаще применяется при построении графиков тригонометрических функций. Поэтому разберем его на двух примерах графиков тригонометрических функций.
1-й пример (на растяжение).
y=sin
Общий метод построения графика:
1) область существования - вся числовая ось;
2) область изменения функции: -1£у£1;
3) функция нечетная, периодическая; период функции найдем из равенства
sin
Следовательно, достаточно построить часть графика для половины периода 0£х£2p;
4) характерные точки:
а) при у=0 sin
б) максимум функции равен 1 при
По этим данным на рисунке 23 построен график заданной функции; сначала график строился для положительного полупериода (утолщенная часть графика), затем на отрезке, соответствующем отрицательному полупериоду, построена косо симметричная кривая (тонкая линия) и, наконец, на остальном протяжении кривая изображена штриховой линией.
График функции y=
| |

линией на рисунке 24. Замечаем, что период исходной функции y=sinx w0=2p, а период заданной функции y=sin
Рис. 23
т. е. вдвое больше периода исходной функции. Таким образом, график, который требуется построить, получится из исходного графика (штрихового, на рисунке 24) путем растяжения его по оси х-ов вдвое.

Рис. 24
2-й пример (на сжатие).
y=sin3x.
Общий метод построения графика тот же, что и в примере первом:
1-й и 2-й пункты исследования те же;
3) период функции находится из равенства
sin3x=sin(3x+2p)=sin3(x+
откуда период w=
4) характерные точки:
а) при у=0 sin3x=0, откуда 3х=
х-ов в точках (0; 0) и (
б) максимум функции равен 1 при 3х=
По этим данным график построен на рисунке 25 в той же последовательности, как и предыдущий график.

Рис. 25.
График функции у=sin3x проще построить методом сжатия по ocи x-ов исходного графика y=sinx в 3 раза (рис. 26), так как период

Рис. 26.
Таким образом, график функции y=f(nx), если известен график функции y=f(x), с строится посредством сжатия по оси х-ов этого исходного графика пропорционально коэффициенту п при аргументе, а именно:
если п>1, то сжатие в п раз;
если 0<п<1, то растяжение в
п.3.2.2 По оси у-ов
1-й пример (на растяжение).
у=2sinx.
Строить этот график методом полного исследования функции нецелесообразно. Отчетливо видно, что ординаты графика в 2 раза больше ординат исходного трафика y=sinx. Поэтому график заданной функции строится путем удвоения всех ординат исходного графика, т.е. путем растяжения исходного графика по оси у-ов 2 раза (рис. 27).
2-й пример (на сжатие).
у=
По тем же соображениям этот график строится способом уменьшения всех ординат исходного графика в 3 раза, т. е. сжатием исходного графика по оси у-ов в 3 раза, что сделано на том же рисунке 27.

Рис. 86.
Таким образом, график функции y=mf(x), если известен график y=f(x), строится посредством растяжения по оси у-ов исходного графика пропорционально коэффициенту т при функции, а именно:
если т>1, то растяжение в т раз;
если 0<т<1, то сжатие в
Примечание 1. Если требуется построить график функции y=mf(nx), то сначала строится штриховой линией график исходной функции у=f(х), а затем этот исходный график сжимается по оси х-ов в п раз и растягивается по оси у-ов в т раз.
Примечание 2. На графиках, разобранных в этой главе, все исходные штриховые линии (первоначальные оси координат, сдвинутые в дальнейшем, и исходные графики) можно стереть или перечеркнуть по окончании всех построений.
§3.3. Отражение.
График функции y=-f(x) получается зеркальным отражением графика функции y=f(x) относительно оси х (рис. 28)
 |
График функции y=f(-x) получается зеркальным отражением графика функции y=f(x) относительно оси у (рис. 29)
 |
Рис. 28. Рис. 29.
 1. Построить график функции
1. Построить график функции Рис. 30
Последовательно строим сначала графики функций у=2f(x),
у=-2f(x), у=-2f(-x) (рис 30, а), а затем графики функции
 |
Рис. 30
§3.4. График суммы и разности двух функций.
Наиболее общий метод построения графиков суммы или разности двух функций заключается в том, что предварительно строятся (штриховыми линиями) два графика для обеих функций, входящих в сумму или разность, затем складываются или вычитаются ординаты этих кривых в характерных точках (пересечение кривых с осями координат, максимумы и минимумы, точки перегиба кривых и т.д.). По полученным точкам строится искомый график и производится проверка несколькими контрольными точками.
Если график суммарной функции имеет экстремум (максимум или минимум), то нахождение точки экстремума средствами элементарной математики возможно только при наличии каких-либо специальных средств заданной функции.
Упрощающие приемы построения графиков суммы и разности функций:
а) Если дана сумма функций, то строится график одной из них, более простой (например, линейной функции); затем к ней пристраивается график второй функции, ординаты которых откладываются от соответствующих точек первого графика.
б) Если задана разность функций, то строится (штриховой линией) график уменьшаемой функции и от нее откладываются ординаты вычитаемой функции, взятые с обратным знаком. Иногда удобно вычертить (штриховой линией) график вычитаемой функции с обратным знаком и ординаты обеих кривых (уменьшаемой функции и вычитаемой с обратным знаком) сложить.
в) Сумма или разность двух функций преобразовывается в одну функцию, если это возможно и если вычерчивание графика такой функции проще.
г) Построение графика алгебраической суммы функций упрощается, если использовать свойства четности, нечетности, периодичности и т.д.
Ниже приводятся примеры, иллюстрирующие как общий прием, так и упомянутые упрощающие приемы построения графиков суммы и разности двух функций.
1. у=х-sinx (рис. 31).

Рис. 31.
Имеем две функции: y1=x и у2=-sinx.
Строим график первой функции, затем от него (а не от оси х-ов) откладываем ординаты второй функции. Для облегчения построения параллельно прямой у1=х проведены две вспомогательные прямые: у=х+1 и у=x-1 На этих прямых находятся вершины синусоиды.
|

2. y=x+tgx (рис. 32).
Построение аналогично построению предыдущего графика.
3. y=x+lgx (рис. 33).
Строится прямая y1=x.
Характерные точки графика:
1) при х=1 y1=l; y=l+lgl=l; точка А(1;1);
2) при х=10 y1=10; y=10+lgl0=ll; точка В(10;11).
Из чертежа можно видеть, что область существования заданной функции (0; ¥), т. е. та же, что и для второго слагаемого у2=lgx.
4. у=х-arcsinx (рис. 34).
Заданная функция нечетная, так как
(-х)-arcsin(-х)=-х+arcsin х=-(x- arcsin x).
Поэтому построение можно выполнить только для правой части графика (при х ³ 0).
Строим два вспомогательных графика:
y1=x и у2=arcsinx.
Ординаты искомого графика представляют собой разность: у1-у2. Характерные точки:
1) х=0, у1=0; у2=0; у=0; точка (0; 0);

рис. 33
 2) х=1 (граничная точка), у1=1, y2=arcsin1=
2) х=1 (граничная точка), у1=1, y2=arcsin1=3) х=0,5, у1=0,5, у2=arcsin0,5=
у=-0,02; точка (0,5;-0,02).
Левая часть графика построена косо симметрично правой.
Из рисунка видно, что область существования заданной функции та же, что для
Рис. 34 второго слагаемого, т. е. для функции y2=arcsinх - сегмент [-1; 1].
5. y=arcctgx-x (рис. 35).
Строим вспомогательные графики:
у1=arcctgх и у2=-х.
Ординаты обоих графиков складываются. Замечаем, что прямая у2=-х является асимптотой заданной кривой. Вторая асимптота

Рис. 35
имеет уравнение: у3=p-х. Характерная точка: при х=0 y=arcctg0=
6. y=sin(arcsinx)-х (рис. 36).
 |
Рис. 36. Рис. 37.
Область существования [-1; 1] заданной функции совпадает с областью существования функции y1=sin(arcsinx). В этой области y1=sin(arcsinx)=x, также и у2=х.
Следовательно, у=у1-у2=0

Рис. 38.
График функции - отрезок оси х-ов в пределах [-1; +1].
7. y=х-ctg(arcctgх) (рис. 37).

Рис. 39.
Область существования заданной функции — вся числовая ось х-ов (-∞; ∞).
у1=х;
y2=ctg(arcctgх)=х;
у=у1+у2=х+х=2х.
График функции — прямая, проходящая через начало координат под углом a к оси х-ов, где
a=arctg2.
8. y=x+arcsin(sinx) (рис. 38).
Заданная функция нечетная. Поэтому построение графика проводим только для х≥0.
Строим полупрямую у1=х и от нее откладываем соответствующие значения функции у2=arcsin(sinх). Левая часть графика строится косо симметрично правой.
9. y=х+arctg(tgx) (рис. 39).
Построение этого графика аналогично построению предыдущего графика.

Рис. 40.
10. у=х-arccos(cosх) (рис. 40). Строим два вспомогательных графика:
у1=х и у2=аrссоs(соsx).
Справа от вертикальной оси ординаты графика заданной функции получаются как разность соответствующих ординат вспомогательных графиков:
y=y1-y2.
Слева от оси у-ов сделано дополнительное построение графика функции - у2= - arccos(cos x). Затем ординаты у1 и (- у2) складываются.

рис. 41.
11. у=х - arcctg (ctg x) (рис. 41).
График этой функции строится так же, как и предыдущий.
12. y=
Вспомогательный график у1=
1) при x=l y1=
2) при х=10 у1=
3)
Область существования заданной функции: (0; ∞), т.е. та же, что и функции y2=lgx.

Рис. 42.
13. у=
Строим графики двух функций (штриховыми линиями): у1=

рис. 43.
14. y=arcsin(sinx)-
Помимо двух вспомогательных графиков функций у1=arcsin(sinx) и у2=
Кроме того, отмечены точки A и В, в которых графики функций у1 и у2 пересекаются, т. е. у=у1-y2=0; эти точки снесены на ось абсцисс.
15. y=
Вспомогательные графики: y1=

Рис. 44.
16. у=ах+а-х при а>1 (черт. 194). Вспомогательные графики: у1=ах и у2=а-х.
 |

Рис. 45. Рис. 46.
При x=0 заданная функция имеет минимум: ymin=a0+a-0= 1+1=2.
Найдем минимум данной функции.
Обозначим ax +a-x=k. (a)
Заметим, что:
1) область существования заданной функции: (-
2) ах>0 и а-x>0 и, следовательно, k>0.
Преобразуем равенство (а):
ax+
Так как ах ≠0, то равенство (б) равносильно равенству: a2x+1=axk, откуда получаем:
а2x-kax+1=0. (в)
Решаем уравнение (в) относительно ах:
Видим, что ах имеет действительное значение при
А так как k>0, то |k|=k и, следовательно, k≥2. Таким образом, kmin=2, т. е.
(ax +a-x)min=2.
Подставляя в равенство (г) значение kmin, находим, что
 Рис. 47 Рис. 47 |
17. y=logacosх+cosx (Рис. 47), где а>1.
Так как заданная функция периодическая, с периодом 2p, то построение проведено для одного периода: -
Вспомогательные функции: y1=cosx и y2=logacosx.
Функция y1=cosx является внутренней для функции y2=logacosx, что учитывается при построении второго графика.
Граничные значения:
при х®(-
y1=cosx®0 и y2=logacosх ®-∞; следовательно, у®-∞.
Характерная точка:
при х=0 у1=соsx=1; y2=logal=0; у=1, точка (0; 1).
При

Рис. 48.
18. y=tgх+logatgх (рис. 48), где а>1.
Строится аналогично предыдущему графику.
Построение проведено, для одного периода (p): 0<х<p.
При
19. у=х+
Функция нечетная, так как
Построение графика проведено для х>0.
Вспомогательные графики: у1=х и у2=
Прямая у1=х является асимптотой искомого графика.
Кроме того, при х>0 функция имеет минимум, который для функций данного вида может быть определен следующим образом.

Рис. 49.
Возьмем функцию в общем виде: у=х+
Так как среднее арифметическое двух положительных чисел больше среднего геометрического этих чисел или ему равно, то


Минимальное значение суммы
x=
Для заданной функции, следовательно, имеем:
Левая ветвь графика косо симметрична правой.
20. у=х-

Рис. 50.
Функция нечетная. Построение проведено для х>0.
Вспомогательные функции: у1=х и у2=-
Ординаты искомого графика получаются алгебраическим сложением ординат у1 и у2. Так как ординаты графика у2 отрицательны, то они откладываются вниз от графика у1.
Прямая у1=х является асимптотой для искомого графика, причем правая ветвь графика приближается к этой асимптоте снизу Кроме того, имеем:
1) при х®0 у=х-
2) при х=1 у1=1; -у2=-1; у=у1 - у2=0.
21. y=sinx+cosx (рис. 51).
 |
Рис. 51.
Преобразуем заданную функцию:
Строим график преобразованной функции:
22. y=cosx- sinx (рис. 52)
 Рис. 52. |
Аналогично предыдущему преобразуем данную функцию:
и строим график функции:
§ 3.5. Графики произведения и частного двух функций
Произведение и частное двух функций поддаются общему исследованию, на основании которого и может быть построен график.
Часто построение графика упрощается, если предварительно построить вспомогательные графики функций, входящих в произведение или частное.
Иногда произведение или частное возможно преобразовать так, что построение графика преобразованной функции оказывается проще.
Эти и некоторые другие приемы построения графиков произведения и частного двух функций иллюстрируются следующими примерами.
1. y=xsinx (Рис. 53).

Рис. 53.
Строятся (штриховыми линиями) вспомогательные графики функций, входящих в заданное произведение: у1=х; y2=sinx.
Перемножение этих графиков упрощается благодаря тому, что функция y2=sinx периодически принимает значения 0 и 1. В первом случае искомый график y=xsinx пересекает ось абсцисс, во втором - касается вспомогательной прямой у1=х.
Так как функция y2=sinx периодически принимает еще значение
(-1), то построение облегчается, если построить еще одну вспомогательную прямую: у3=-х (на рисунке эта прямая построена штрих-пунктирной линией).
Для всех х=2 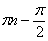
заданный график касается этой вспомогательной прямой, так как для этих значений х
sinx=-1.
Так как заданная функция y=xsinx четная [(-x)sin(-х)=
=(-х)(-sinx)=xsinx], то указанное построение проводится только для правой части графика; левая часть графика строится затем симметрично правой.

Рис. 54.
2. у= -хcosx (Рис. 54).
Так же, как и в предыдущем случае, помимо графиков двух вспомогательных функций: у1=-х и y2=cosx, входящих в заданное произведение, построен еще третий вспомогательный график функции: у3=х.
Далее построение аналогично предыдущему.
3. y= 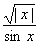
(Рис. 55).
Замечаем, что заданная функция нечетная, так как 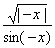
= 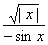
=
=- 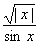
. Поэтому построение проводится только для правой части графика, левая часть графика строится затем косо симметрично правой.
На чертеже построены два графика вспомогательных функций, входящих в. заданное частное: 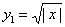
и y2=sinx, и третий вспомогательный график: у3=- 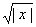
.
Остальные построения аналогичны предыдущим.

Рис. 55.
Следует особо объяснить вид графика при х®0, так как в этом случае получается неопределенность вида 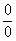
, которую следует раскрыть.
Известно, что 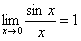
, т. е. что при x®0sinx~х. Следовательно, можно записать: 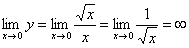
4. 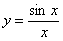
(Рис. 56).
Функция четная, так как 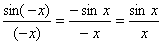
.
Вспомогательные функции: y1=sinx; у2= 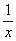
и y3= 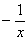
Заданный график строится как график произведения: у1y2=sinx 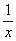
.

Рис. 56.
5. y=axlogbx, где а>0; а≠1 и b>1 (Рис. 57).
 Вспомогательные функции: у1=ах; y2=logb x.
Вспомогательные функции: у1=ах; y2=logb x.
Так как область существования функции у2=logb x есть интервал (0, ¥), что определяет область существования заданной функции, то и график вспомогательной функции y1=ах построен только для х>0.
Заметим, что при x=b y2=logbb=l и у=у1у2=аb, получаем точку А(b;аb).
6. у=|х| 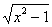
(рис. 58).
Функция четная. Построение проводится для правой части графика; левая часть графика симметрична правой.
Вспомогательные графики: у1 =|х|; у2= 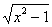
.
При x=± 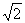
у2= 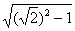
=1, поэтому график заданной функции пересекает прямую y1=|х| в точке A( 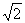
, 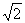
).
При х=±1 у2=0 и у=0.

Рис. 58.
7. 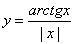
(Рис. 59).
Функция нечетная, так как
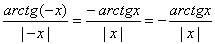
Вспомогательные графики функций y1=arctgх и у2=|х| пoстроены только для х>0.

Рис. 59.
Характерные точки (для правой части графика):
1) 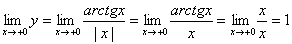
так как при х®0 tgx»x;
2) 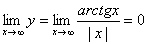
;
3) при х= 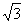
y= 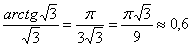
; точка (1,7; 0,6).
8. у= 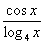
(Рис. 60).
Вспомогательные графики: у1=соsх; y2=log4x. Находим область существования заданной функции.
Числитель у1=соsх не дает никаких ограничений для х.

Рис. 60.
Знаменатель y2=log4x обусловливает:
а) х>0,
б) log4x≠0, т. е. х≠1.
Следовательно, область существования заданной функции состоит из двух интервалов: (0; 1) и (1; ∞).
Так как х>0, то и вспомогательный график у1 строится только для правой полуплоскости.
Характерные точки:
1) 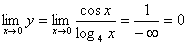
2) 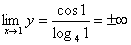
. Прямая x= 1 является асимптотой графика;
3) при x=4 y2=log44=l, поэтому искомый график пересекает график вспомогательной функции у1 при x=4;
4) при х= 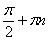
у1=соsx=0, у=0 - в этих точках заданный график пересекает ось абсцисс.
График колеблется около оси абсцисс, приближаясь к ней.
Список использованных источников и литературы
1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: Учеб. для 7 кл. сред шк. – 3-е изд. – М.: Просвещение, 1993..
2. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: Учеб. для 8 кл. сред шк. – 3-е изд. – М.: Просвещение, 1994.
3. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: Учеб. для 9 кл. сред шк. – 3-е изд. – М.: Просвещение, 1995.
4. Колмогоров А.Н., Абрамов А.М., Вейц Б.Е., Ивашев - Мусатов О.С., Ивлев Б.М., Шварцбурд С.И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред шк. – 5-е изд. – М.: Просвещение, 1997.
5. Денищева Л.О., Дудницын Ю.П., Ивлев Б.М., и др. Алгебра и начала анализа в 9-10 классах: Пособие для учителя – М.: Просвещение, 1988.
6. Алимов Ш.А., Колягин Ю.М. Сидоров Ю.В. Алгебра: Учеб. для 7 кл. сред шк. – 3-е изд. – М.: Просвещение, 1995.
7. Алимов Ш.А., Колягин Ю.М. Сидоров Ю.В. Алгебра: Учеб. для 8 кл. сред шк. – 3-е изд. – М.: Просвещение, 1996.
8. Алимов Ш.А., Колягин Ю.М. Сидоров Ю.В. Алгебра: Учеб. для 9 кл. сред шк. – 4-е изд. – М.: Просвещение, 1998.
9. Алимов Ш.А., Колягин Ю.М. Сидоров Ю.В. Алгебра: Учеб. для 10-11 кл. сред шк. – 6-е изд. – М.: Просвещение, 1998.
10. Мордкович А.Г. Алгебра – 7. Учебник. – 4-е изд. – М.: Мнемозина, 2003.
11. Мордкович А.Г. Алгебра – 8. Учебник. – 4-е изд. – М.: Мнемозина, 2003.
12. Мордкович А.Г. Алгебра – 9. Учебник. – 4-е изд. – М.: Мнемозина, 2003.
13. Мордкович А.Г. Алгебра и начала анализа– 10-11. Учебник. – 4-е изд. – М.: Мнемозина, 2003.
14. Мордкович А.Г. Алгебра – 7-9. Учебное пособие для учителя. – 2-е изд. – М.: Мнемозина, 2001.
15. Мордкович А.Г. Алгебра – 10-11. Учебное пособие для учителя. – 2-е изд. – М.: Мнемозина, 2001.
16. Г. И. Глейзер, История математики в школе, IX-X классы, Москва, Просвещение, 1983.
17. Л. С. Понтрягин, Математический анализ для школьников, Москва, Наука, 1983.
18. В. С. Крамор, Повторяем и систематизируем школьный курс алгебры и начал анализа, Москва, Просвещение, 1990.
19. Гурский И.П. Функции и построение графиков. Пособие для учителей. – М.: Просвещение, 1968.
20. Вилейтнер Г. История математики от Декарта до середины XIX столетия. – Москва. 1969.
21. К. А. Рыбников, Возникновение и развитие математической науки, Москва, Просвещение, 1987.
22. Н. И. Борисов, Как обучать математике, Москва, Просвещение, 1979.
23. С.Г. Крейн, В. Н. Ушаков, Математический анализ элементарных функций, Москва, Наука, 1966.
24. Кузнецова Г.М., Миндюк Н.Г. Программы для общеобразоват. школ, гимназий, лицеев. – М.: Дрофа, 2002.
sinx=-1.
Так как заданная функция y=xsinx четная [(-x)sin(-х)=
=(-х)(-sinx)=xsinx], то указанное построение проводится только для правой части графика; левая часть графика строится затем симметрично правой.

Рис. 54.
2. у= -хcosx (Рис. 54).
Так же, как и в предыдущем случае, помимо графиков двух вспомогательных функций: у1=-х и y2=cosx, входящих в заданное произведение, построен еще третий вспомогательный график функции: у3=х.
Далее построение аналогично предыдущему.
3. y=
Замечаем, что заданная функция нечетная, так как
=-
На чертеже построены два графика вспомогательных функций, входящих в. заданное частное:
Остальные построения аналогичны предыдущим.

Рис. 55.
Следует особо объяснить вид графика при х®0, так как в этом случае получается неопределенность вида
Известно, что
4.
Функция четная, так как
Вспомогательные функции: y1=sinx; у2=
Заданный график строится как график произведения: у1y2=sinx

Рис. 56.
5. y=axlogbx, где а>0; а≠1 и b>1 (Рис. 57).
 Вспомогательные функции: у1=ах; y2=logb x.
Вспомогательные функции: у1=ах; y2=logb x. Так как область существования функции у2=logb x есть интервал (0, ¥), что определяет область существования заданной функции, то и график вспомогательной функции y1=ах построен только для х>0.
|
6. у=|х|
Функция четная. Построение проводится для правой части графика; левая часть графика симметрична правой.
Вспомогательные графики: у1 =|х|; у2=
При x=±
При х=±1 у2=0 и у=0.

Рис. 58.
7.
Функция нечетная, так как
Вспомогательные графики функций y1=arctgх и у2=|х| пoстроены только для х>0.

Рис. 59.
Характерные точки (для правой части графика):
1)
так как при х®0 tgx»x;
2)
3) при х=
8. у=
Вспомогательные графики: у1=соsх; y2=log4x. Находим область существования заданной функции.
Числитель у1=соsх не дает никаких ограничений для х.

Рис. 60.
Знаменатель y2=log4x обусловливает:
а) х>0,
б) log4x≠0, т. е. х≠1.
Следовательно, область существования заданной функции состоит из двух интервалов: (0; 1) и (1; ∞).
Так как х>0, то и вспомогательный график у1 строится только для правой полуплоскости.
Характерные точки:
1)
2)
3) при x=4 y2=log44=l, поэтому искомый график пересекает график вспомогательной функции у1 при x=4;
4) при х=
График колеблется около оси абсцисс, приближаясь к ней.
Список использованных источников и литературы
1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: Учеб. для 7 кл. сред шк. – 3-е изд. – М.: Просвещение, 1993..
2. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: Учеб. для 8 кл. сред шк. – 3-е изд. – М.: Просвещение, 1994.
3. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: Учеб. для 9 кл. сред шк. – 3-е изд. – М.: Просвещение, 1995.
4. Колмогоров А.Н., Абрамов А.М., Вейц Б.Е., Ивашев - Мусатов О.С., Ивлев Б.М., Шварцбурд С.И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред шк. – 5-е изд. – М.: Просвещение, 1997.
5. Денищева Л.О., Дудницын Ю.П., Ивлев Б.М., и др. Алгебра и начала анализа в 9-10 классах: Пособие для учителя – М.: Просвещение, 1988.
6. Алимов Ш.А., Колягин Ю.М. Сидоров Ю.В. Алгебра: Учеб. для 7 кл. сред шк. – 3-е изд. – М.: Просвещение, 1995.
7. Алимов Ш.А., Колягин Ю.М. Сидоров Ю.В. Алгебра: Учеб. для 8 кл. сред шк. – 3-е изд. – М.: Просвещение, 1996.
8. Алимов Ш.А., Колягин Ю.М. Сидоров Ю.В. Алгебра: Учеб. для 9 кл. сред шк. – 4-е изд. – М.: Просвещение, 1998.
9. Алимов Ш.А., Колягин Ю.М. Сидоров Ю.В. Алгебра: Учеб. для 10-11 кл. сред шк. – 6-е изд. – М.: Просвещение, 1998.
10. Мордкович А.Г. Алгебра – 7. Учебник. – 4-е изд. – М.: Мнемозина, 2003.
11. Мордкович А.Г. Алгебра – 8. Учебник. – 4-е изд. – М.: Мнемозина, 2003.
12. Мордкович А.Г. Алгебра – 9. Учебник. – 4-е изд. – М.: Мнемозина, 2003.
13. Мордкович А.Г. Алгебра и начала анализа– 10-11. Учебник. – 4-е изд. – М.: Мнемозина, 2003.
14. Мордкович А.Г. Алгебра – 7-9. Учебное пособие для учителя. – 2-е изд. – М.: Мнемозина, 2001.
15. Мордкович А.Г. Алгебра – 10-11. Учебное пособие для учителя. – 2-е изд. – М.: Мнемозина, 2001.
16. Г. И. Глейзер, История математики в школе, IX-X классы, Москва, Просвещение, 1983.
17. Л. С. Понтрягин, Математический анализ для школьников, Москва, Наука, 1983.
18. В. С. Крамор, Повторяем и систематизируем школьный курс алгебры и начал анализа, Москва, Просвещение, 1990.
19. Гурский И.П. Функции и построение графиков. Пособие для учителей. – М.: Просвещение, 1968.
20. Вилейтнер Г. История математики от Декарта до середины XIX столетия. – Москва. 1969.
21. К. А. Рыбников, Возникновение и развитие математической науки, Москва, Просвещение, 1987.
22. Н. И. Борисов, Как обучать математике, Москва, Просвещение, 1979.
23. С.Г. Крейн, В. Н. Ушаков, Математический анализ элементарных функций, Москва, Наука, 1966.
24. Кузнецова Г.М., Миндюк Н.Г. Программы для общеобразоват. школ, гимназий, лицеев. – М.: Дрофа, 2002.