Контрольная работа на тему Исследование операций
Работа добавлена на сайт bukvasha.net: 2014-07-03Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Курсовая работа по дисциплине «Исследование операций»
Нормоконтроллёр:
Плотникова Н. В. _______
«____» ___________ 2005 г.
Руководитель:
Плотникова Н. В. _______
«____» ___________ 2005 г.
Автор:
Студент группы ПС-346
Нечаев Л. В. ___________
«____» ___________ 2005 г.
Работа защищена
с оценкой______________
«____» ___________ 2005 г.
Нормоконтроллёр:
Плотникова Н. В. _______
«____» ___________ 2005 г.
Руководитель:
Плотникова Н. В. _______
«____» ___________ 2005 г.
Автор:
Студент группы ПС-346
Нечаев Л. В. ___________
«____» ___________ 2005 г.
Работа защищена
с оценкой______________
«____» ___________ 2005 г.
Оглавление
\f "1-9" \t "Заголовок 2;2;Заголовок 1;1;Заголовок 1;1;Заголовок 2;2" Задача 1............................................................................................................................................. 3
Условие......................................................................................................................................... 3
Решение....................................................................................................................................... 3
Ответ: ............................................................................................................................................ 5
Задача 2............................................................................................................................................. 6
Условие......................................................................................................................................... 6
Решение....................................................................................................................................... 6
Ответ:............................................................................................................................................. 8
Примечание:................................................................................................................................ 8
Задача 3........................................................................................................................................... 10
Условие....................................................................................................................................... 10
Решение..................................................................................................................................... 10
Ответ:........................................................................................................................................... 14
Задача 4........................................................................................................................................... 15
Условие....................................................................................................................................... 15
Решение..................................................................................................................................... 15
Ответ:........................................................................................................................................... 19
Приложение 1................................................................................................................................ 20
Список использованной литературы...................................................................................... 22
Условие......................................................................................................................................... 3
Решение....................................................................................................................................... 3
Ответ: ............................................................................................................................................ 5
Задача 2............................................................................................................................................. 6
Условие......................................................................................................................................... 6
Решение....................................................................................................................................... 6
Ответ:............................................................................................................................................. 8
Примечание:................................................................................................................................ 8
Задача 3........................................................................................................................................... 10
Условие....................................................................................................................................... 10
Решение..................................................................................................................................... 10
Ответ:........................................................................................................................................... 14
Задача 4........................................................................................................................................... 15
Условие....................................................................................................................................... 15
Решение..................................................................................................................................... 15
Ответ:........................................................................................................................................... 19
Приложение 1................................................................................................................................ 20
Список использованной литературы...................................................................................... 22
Задача 1
Условие
Оператор связи оказывает 2 вида услуг:1. Предоставление одной линии телефонной сети общего пользования (ТСОП) и трёх линий цифровой связи (ЦС);
2. Предоставление одной линии ЦС и двух линий ТСОП.
Стоимость услуг указана в табл. 1:
Таблица 1
| ТСОП | ЦС | Цена | |
| Услуга 1 | 1 | 3 | 750 |
| Услуга 2 | 2 | 1 | 600 |
ТСОП ≤ 300
ЦС ≤ 120
ТСОП+2*ЦС ≤ 380
Определить оптимальное соотношение услуг 1 и 2, которые оператор должен предоставлять для получения максимальной выручки.
Решение
1. Обозначим за x1 количество оказанных услуг с номером `1', а x2 – количество оказанных услуг с номером `2'.2. Учтём ограничения задачи:

3. Составим целевую функцию, которую нужно максимизировать:
4. Задача сведена к следующей задаче линейного программирования: «Найти значения аргументов x1 и x2, при которых функция
5. Решим выше представленную задачу графическим методом, так как в задаче присутствуют только 2 переменные x1 и x2. Для этого:
Изобразим многоугольник решений в плоскости x2Ox1:

График представлен на рис. 1.
SHAPE
| |
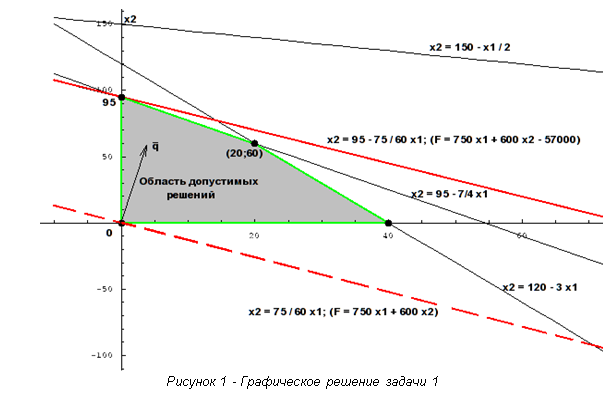
В начале максимизации наибольшее значение целевой функции равно 0, также F проходит через начало координат (пунктирная линия на рис. 1). Вектор
Оптимальное решение находится в точке (0; 95), находящейся на
пересечении прямых
Итак, для получения наибольшей прибыли (57000 ед.) оператор связи должен не предоставлять услуг 1, а услуг 2 предоставить в количестве 95 штук.
Ответ:
– Не предоставлять yслуг #1– Yслуг #2 предоставить в количестве 95 штук.
Задача 2
Условие
Решение задачи линейного программирования.С помощью симплекс–таблиц найти решение задачи линейного программирования: определить экстремальное значение целевой функции F=CTx при условии Ax B,
где CT = [ c1 c2 . . . c6 ]T , ВT = [ b1 b2 . . . b6 ]T , XT = [ x1 x2 . . . x6]T , А= [aij] (i=1,6; j=1,3).
Таблица 2
| c1 | c2 | c3 | c4 | c5 | c6 | b1 | b2 | b3 | Знаки ограничений | ||
| 1 | 2 | 3 | |||||||||
| 4 | -1 | 12 | 2 | -1 | 0 | 2 | 13 | 16 | = | = | = |
| a11 | a12 | a13 | a14 | a15 | a16 | a21 | a22 | a23 | a24 | a25 | a26 | a31 | a32 | a33 | a34 | a35 | a36 | Ext |
| -1 | 1 | 1 | 0 | 0 | 0 | 4 | 3 | 2 | 1 | 1 | 0 | 3 | 2 | 0 | 0 | 1 | 0 | max |
Решение
Составляем систему:
Целевая функция имеет вид
Приведем систему ограничений к виду основной задачи линейного программирования:

Пусть х1, х2 – свободные переменные, х3, х4, х5 – базисные.
Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:

Составляем симплекс-таблицу.
Это решение является допустимым, но не опорным, т.к. присутствует отрицательный свободный член во второй строке. Ликвидируем его путём замены базисных переменных на основные. В строке x4 находится отрицательный элемент a42=-2, следовательно, столбец x2 – разрешающий. Наименьшее отношение между свободным членом и эл-том разрешающего столбца (см. поле «оценка») будет в первой строке и элемент a32 – разрешающий. Получилась таблица 3 (верхние числа).
Таблица 3
| Базис | Свободный член | Переменные | Оценка | |
| x1 | x2 | |||
| x3 | 2 2 | -1 -1 | 1 1 | 2 |
| x4 | -7 4 | 3 -2 | -2 2 | - |
| x5 | 16 -4 | 3 2 | 2 -2 | 8 |
| F | 6 18 | 13 -9 | -9 9 | - |
1. Выделим разрешающий элемент aij;
2. Найдём обратную ему величину λ=1/aij и запишем её в правом нижнем углу этой же ячейки;
3. Все элементы разрешающей строки, кроме разрешающего элемента, умножим на λ и запишем внизу соответствующей ячейки;
4. Все элементы разрешающего столбца , кроме разрешающего элемента, умножим на -λ и запишем внизу соответствующей ячейки;
5. Выделим все верхние числа в разрешающей строке, и все нижние - в разрешающем столбце;
6. Для каждого из остальных элементов запишем в нижнюю часть ячейки произведение выделенных чисел, стоящих в той же строке и в том же столбце, что и данный элемент;
7. Перепишем таблицу, заменив переменные: элементы разрешающих строки и столбца – значениями, стоящими в нижних частях этих ячеек; оставшиеся элементы – суммой чисел, стоящих в верхних и нижних частях ячеек.
Применительно к текущему шагу, разрешающий элемент a32, λ = 1 / a32 = 1. После указанных выше преобразований, получим новую таблицу (табл. 4):
Таблица 4
| Базис | Свободный член | Переменные | ||
| x1 | x3 | |||
| x2 | 2 | -1 | 1 | |
| x4 | -3 | 1 | 2 | |
| x5 | 12 | 5 | -2 | |
| F | 24 | 4 | 9 | |
Ответ:
Система уравнений несовместима в области положительных значений переменных.Примечание:
Этот же результат получен и при решении данной задачи в пакете Mathematica:
Задача 3
Условие
Решение транспортной задачи:1. Записать условия задачи в матричной форме.
2. Определить опорный план задачи.
3. Определить оптимальный план задачи.
4. Проверить решение задачи методом потенциалов.
Таблица 5
| B1 | B2 | B3 | ai | |
| A1 | 10 | 20 | 32 | 700 |
| A2 | 12 | 50 | 25 | 600 |
| A3 | 21 | 18 | 50 | 200 |
| A4 | 25 | 15 | 23 | 200 |
| A5 | 21 | 30 | 40 | 100 |
| bj | 300 | 700 | 1000 |
Решение
Заметим, что общее количество запасов (700+600+200+200+100=1800) меньше количества заявок (300+700+1000=2000), следовательно имеем открытую транспортную задачу с избытком заявок. Добавим строку с фиктивными запасами для дополнения задачи до задачи закрытого типа. После корректировки получаем транспортную задачу с правильным балансом (табл. 6):Таблица 6
| B1 | B2 | B3 | ai | |
| A1 | 10 | 20 | 32 | 700 |
| A2 | 12 | 50 | 25 | 600 |
| A3 | 21 | 18 | 50 | 200 |
| A4 | 25 | 15 | 23 | 200 |
| A5 | 21 | 30 | 40 | 100 |
| A6 | 0 | 0 | 0 | 200 |
| bj | 300 | 700 | 1000 | 2000 |
Таблица 7
| B1 | B2 | B3 | ai | ||
| A1 | 10 300 | 20 400 | 32 - | 700 | -10 (2) |
| A2 | 12 - | 50 - | 25 600 | 600 | -7 (7) |
| A3 | 21 - | 18 200 | 50 - | 200 | -8 (4) |
| A4 | 25 - | 15 100 | 23 100 | 200 | -5 (5) |
| A5 | 21 - | 30 - | 40 100 | 100 | -22 (8) |
| A6 | 0 - | 0 - | 0 200 | 200 | 18 (9) |
| Bj | 300 | 700 | 1000 | 2000 | |
| 0 (1) | -10 (3) | -18 (6) |
Первоначально затраты на перевозку составят:
Составим матрицу оценок методом потенциалов:
Начнём с первого столбца. Пусть потенциал этого столбца равен нулю. Рядом с потенциалом в скобках записываем номер шага. После прибавления потенциала к коэффициентам затрат первого столбца коэффициент затрат заполненной клетки (1;1) не изменится; чтобы полученный после сложения коэффициент стал равен 0, потенциал первой строки таблицы должен быть равен -10; для обнуления коэффициента затрат клетки (1;2) потенциал второго столбца должен быть -10 и т.д.
Изменённые коэффициенты выписываются в виде матрицы оценок:

Критерий оптимальности (базисное распределение поставок верно тогда и только тогда, когда оценки всех свободных клеток неотрицательны) на данном шаге не выполнен – присутствуют 2 свободные клетки с отрицательными оценками.
Продолжим оптимизацию (табл. 8). Составим цикл пересчёта для клетки (5;2) и дадим поставку неё:
Таблица 8
| B1 | B2 | B3 | ai | |
| A1 | 10 300 | 20 400 | 32 - | 700 |
| A2 | 12 - | 50 - | 25 600 | 600 |
| A3 | 21 - | 18 200 | 50 - | 200 |
| A4 | 25 - |  15 - 15 - 100 | 23 + 100 | 200 |
| A5 | 21 - | 30 + - | 40 - 100 | 100 |
| A6 | 0 - | 0 - | 0 200 | 200 |
| Bj | 300 | 700 | 1000 | 2000 |
Таблица 9
| B1 | B2 | B3 | ai | ||
| A1 | 10 300 | 20 400 | 32 - | 700 | -10 (2) |
| A2 | 12 - | 50 - | 25 600 | 600 | -7 (8) |
| A3 | 21 - | 18 200 | 50 - | 200 | -8 (4) |
| A4 | 25 - | 15 0 | 23 200 | 200 | -5 (5) |
| A5 | 21 - | 30 100 | 40 - | 100 | -20 (6) |
| A6 | 0 - | 0 - | 0 200 | 200 | 18 (9) |
| Bj | 300 | 700 | 1000 | 2000 | |
| 0 (1) | -10 (3) | -18 (7) |
После передвижения освободились сразу 2 клетки, решение перестало быть базисным. Для того, чтобы оно осталось базисным, дадим фиктивную поставку в клетку (4;2).
Снова составляем матрицу оценок по вышеприведённому алгоритму:
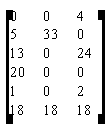
На текущем шаге клеток с отрицательной оценкой нет, следовательно, критерий оптимальности выполнен.
Проверим решение с помощью метода потенциалов (табл. 10). Примем a1 = 0, тогда bj = cij – ai (для заполненных клеток). Если найденное решение справедливо, то во всех пустых клетках таблицы Δij = cij – (ai + bj ) ≥ 0, и Δij = 0 в заполненных клетках. Получим следующую таблицу (в скобках показаны оценки клеток):
Таблица 9
Условие Δij ≥ 0 выполняется, следовательно, решение верное.
Суммарные затраты на перевозку составляют:
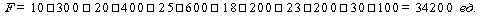
Определить экстремум целевой функции вида
F = c11x12+c22x22+c12x1x2+b1x1+b2x2
при условиях
a11x1+a12x2<=>p1
a21x1+a22x2<=>p2 .
Данные располагаются в табл. 11.
1. Найти стационарную точку целевой функции и исследовать ее (функцию) на выпуклость (вогнутость) в окрестностях стационарной точки.
2. Составить функцию Лагранжа.
3. Получить систему неравенств в соответствии с теоремой Куна-Таккера.
4. Используя метод искусственных переменных составить симплекс-таблицу и найти решение полученной задачи линейного программирования.
5. Дать ответ с учетом условий дополняющей нежёсткости.
Таблица 11
Ограничения:
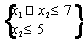
, 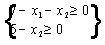
1. Определим относительный максимум функции. Для этого необходимы координаты стационарной точки 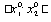
.
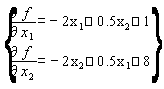
, 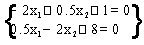
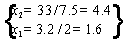
Получили стационарную точку (1.6;4.4).
2. Исследуем стационарную точку на максимум, для чего и определим вогнутость функции f.
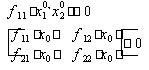
, 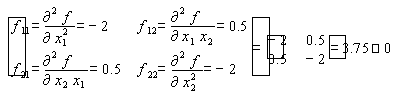
Условия выполняются, следовательно целевая функция является строго вогнутой в окрестности стационарной точки.
3. Составим функцию Лагранжа:
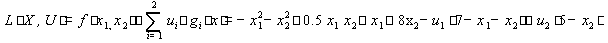
Составим систему неравенств в соответствии с теоремой Куна-Таккера.
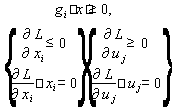
А) 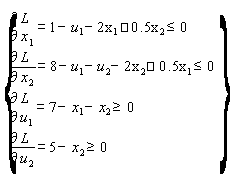
Б) 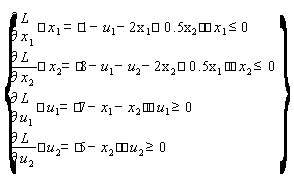
Перепишем систему А:
A1) 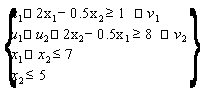
.Вводим дополнительные переменные v1, v2, w1, w2, превращающие неравенства системы А1 в равенства: 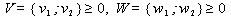
A2) 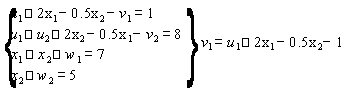
перепишем систему Б:
Б2) 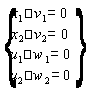
- условия дополняющей нежёсткости
Решим систему А2 с помощью метода искусственных переменных. 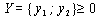
в первое и второе уравнение системы А2.
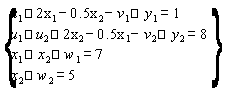
Вводим псевдоцелевую функцию
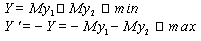
базисные переменные: y1, y2, w1, w2
свободные переменные: x1, x2, v1, v2, u1, u2
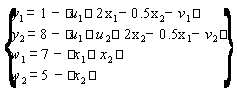
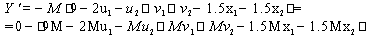
Решаем эту задачу симплекс-методом с помощью таблиц и небольшой программы на языке Си, текст которой приведён в Приложении 1.
Таблица 12
Таблица 13
Таблица 14
Оптимальное решение:
y1=y2=u1=u2=v1=v2=0
x1=1.6
x2=4.4
w1=1
w2=0.6
Проверим условие дополняющей нежёсткости:
xi*vi=0
ui*wi=0
Условия выполняются, следовательно, x1=1.6, x2=4.4 являются решением исходной задачи kвадратичного программирования. Координаты стационарной точки совпадают с координатами, полученных в качестве ответа. Стационарная точка удовлетворяет условиям ограничений.
Значение функции в точке (x1;x2) равно 0.
x2=4.4
f(x1;x2) = 0
#include <stdio.h>
#define x 7
#define y 5
double mc[x*y] =
{
1, 2, -0.5, 1, 0, -1, 0,
8, -0.5, 2, 1, 1, 0, -1,
7, 1, 1, 0, 0, 0, 0,
5, 0, 1, 0, 0, 0, 0,
9, -1.5, -1.5, -2, -1, 1, 1
};
double mt[x*y];
void mprint (double* m, int xs, int ys)
{
int i, j;
printf ("\n");
for (j = 0; j < ys; j++)
{
for (i = 0; i < xs; i++)
{
printf ("%10.4lg ", m[j*xs+i]);
}
printf ("\n");
}
}
int main (void)
{
int i, j, i1, j1, it, jt;
double msx, msx1;
// Выбираем разрешающий эл-т
nextmtx:
printf ("\nИсходная матрица коэффициентов:"); mprint (mc, x, y);
getch ();
msx = 10000.;
for (i = 0; i < x; i++)
{
if (mc[(y-1)*x+i] < 0)
{
// Возможно, найден разрешающий столбец
for (j = 0; j < y; j++)
{
// Ищем наименьшее отношение своб. члена к эл-ту разр. столбца
if (mc[j*x+i] < 1e-32)
continue; // Нулевой или отрицательный
msx1 = mc[j*x] / mc[j*x+i];
if (msx > msx1) // Частное св.ч / р.эл
{
msx = msx1; // наименьшее ищем
it = i; jt = j; // координаты р.эл.
}
}
if (msx > 9999.) continue; // Нет положительных эл-тов
else // найден р.эл., mx != 0
{
i = it; j = jt; // его координаты
}
printf ("\n Разрешающий элемент: a(%d;%d) = %lg", j+1, i+1, mc[j*x+i]);
if (mc[j*x+i] > 0)
{
// Это и есть разрешающий элемент (s_el), находим обратную величину
mt[j*x+i] = 1. / mc[j*x+i];
for (i1 = 0; i1 < x; i1++)
{
// Разрешающая строка ( 1/s_el)
if (i1 == i) continue; // Пропустить сам s_el
mt[j*x+i1] = mt[j*x+i] * mc[j*x+i1];
}
for (j1 = 0; j1 < y; j1++)
{
// Разрешающий столбец (-1/s_el)
if (j1 == j) continue; // Пропустить сам s_el
mt[j1*x+i] = - mt[j*x+i] * mc[j1*x+i];
}
// успешно составлены разр. строка и столбец.
// теперь составляем остальные коэфф-ты
for (j1 = 0; j1 < y; j1++)
{
if (j1 == j) continue; // Пропустить всю разреш. строку
for (i1 = 0; i1 < x; i1++)
{
if (i1 == i) continue; // И столбец тоже
// Произведение нижней части столбца
// на верхнюю часть строки
mt[j1*x+i1] = mt[j1*x+i] * mc[j*x+i1];
}
}
/*
* Всё. Готова матрица нижних значений, теперь нужно
* поместить всё на свои места в mc
*/
printf ("\nМатрица нижних значений:"); mprint (mt, x, y);
getch ();
for (j1 = 0; j1 < y; j1++)
{
for (i1 = 0; i1 < x; i1++)
{
if ((j1 == j) || (i1 == i))
{
/*
* Разрешающая строка или столбец
* просто ложим элементы в mc
*/
mc[j1*x+i1] = mt[j1*x+i1];
}
else
// иначе - сумму
mc[j1*x+i1] += mt[j1*x+i1];
}
}
// Всё готово к очередному шагу.
goto nextmtx; // след. матрица
}
// Этот эл-т не подходит, т.к. он отрицательный
}
// Если так и не было подходящего эл-та, то проверяем след. столбец
}
// отрицательны коэфф-тов при целевой ф-ции не найдено, следовательно, решение оптимально
printf ("\nОптимизировано. Ответ:"); mprint (mc, x, y);
return 0;
}
Программа компилировалась командной строкой:
gcc simplex.c -o simplex
, запускалась:
./simplex
и выдавала на консоль пошаговое решение задачи, которое было занесено в симплекс-таблицы (см. табл. 12-14) четвёртой задачи данной курсовой работы.
2. Плотникова Н. В. Курс лекций (ПС)
Снова составляем матрицу оценок по вышеприведённому алгоритму:

На текущем шаге клеток с отрицательной оценкой нет, следовательно, критерий оптимальности выполнен.
Проверим решение с помощью метода потенциалов (табл. 10). Примем a1 = 0, тогда bj = cij – ai (для заполненных клеток). Если найденное решение справедливо, то во всех пустых клетках таблицы Δij = cij – (ai + bj ) ≥ 0, и Δij = 0 в заполненных клетках. Получим следующую таблицу (в скобках показаны оценки клеток):
Таблица 9
| B1 | B2 | B3 | ai | ||
| A1 | 10 (0) 300 | 20 (0) 400 | 32 (4) - | 700 | -10 (2) |
| A2 | 12 (5) - | 50 (33) - | 25 (0) 600 | 600 | -7 (8) |
| A3 | 21 (13) - | 18 (0) 200 | 50 (24) - | 200 | -8 (4) |
| A4 | 25 (20) - | 15 (0) 0 | 23 (0) 200 | 200 | -5 (5) |
| A5 | 21 (1) - | 30 (0) 100 | 40 (2) - | 100 | -20 (6) |
| Bj | 300 | 700 | 1000 | ||
| 0 (1) | -10 (3) | -18 (7) |
Ответ:
Таблица 10| B1 | B2 | B3 | ai | |
| A1 | 10 300 | 20 400 | 32 - | 700 |
| A2 | 12 - | 50 - | 25 600 | 600 |
| A3 | 21 - | 18 200 | 50 - | 200 |
| A4 | 25 - | 15 - | 23 200 | 200 |
| A5 | 21 - | 30 100 | 40 - | 100 |
| Bj | 300 | 700 | 1000 | 1800/2000 |
Задача 4
Условие
Решение задачи нелинейного программированияОпределить экстремум целевой функции вида
F = c11x12+c22x22+c12x1x2+b1x1+b2x2
при условиях
a11x1+a12x2<=>p1
a21x1+a22x2<=>p2 .
Данные располагаются в табл. 11.
1. Найти стационарную точку целевой функции и исследовать ее (функцию) на выпуклость (вогнутость) в окрестностях стационарной точки.
2. Составить функцию Лагранжа.
3. Получить систему неравенств в соответствии с теоремой Куна-Таккера.
4. Используя метод искусственных переменных составить симплекс-таблицу и найти решение полученной задачи линейного программирования.
5. Дать ответ с учетом условий дополняющей нежёсткости.
Таблица 11
| b1 | b2 | c11 | c12 | c22 | extr | a11 | a12 | a21 | a22 | p1 | p2 | Знаки огр. | |
| 1 | 2 | ||||||||||||
| 1 | 8 | -1 | 0.5 | -1 | max | 1 | 1 | 0 | 1 | 7 | 5 | ≤ | ≤ |
Решение
Целевая функция имеет вид:Ограничения:
1. Определим относительный максимум функции. Для этого необходимы координаты стационарной точки
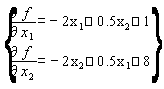
Получили стационарную точку (1.6;4.4).
2. Исследуем стационарную точку на максимум, для чего и определим вогнутость функции f.
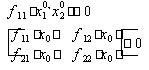
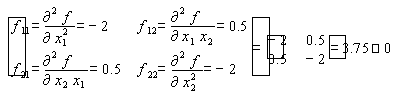
Условия выполняются, следовательно целевая функция является строго вогнутой в окрестности стационарной точки.
3. Составим функцию Лагранжа:
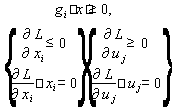
А)
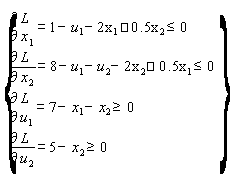
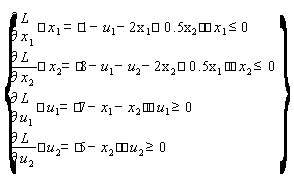
Перепишем систему А:
A1)
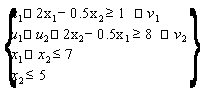
A2)
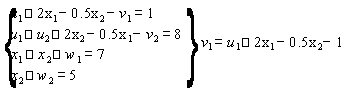
перепишем систему Б:
Б2)
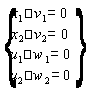
Решим систему А2 с помощью метода искусственных переменных.
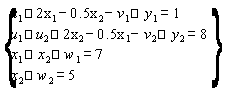
Вводим псевдоцелевую функцию
базисные переменные: y1, y2, w1, w2
свободные переменные: x1, x2, v1, v2, u1, u2
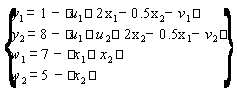
Решаем эту задачу симплекс-методом с помощью таблиц и небольшой программы на языке Си, текст которой приведён в Приложении 1.
Таблица 12
| bi | x1 | x2 | u1 | u2 | v1 | v2 | |
| y1 | 1 0.5 | 2 0.5 | -0.5 -0.25 | 1 0.5 | 0 0 | -1 -0.5 | 0 0 |
| y2 | 8 0.25 | -0.5 0.25 | 2 -0.125 | 1 0.25 | 1 0 | 0 -0.25 | -1 0 |
| w1 | 7 -0.5 | 1 -0.5 | 1 0.25 | 0 -0.5 | 0 0 | 0 0.5 | 0 0 |
| w2 | 5 0 | 0 0 | 1 0 | 0 0 | 0 0 | 0 0 | 0 0 |
| Y' | 9M 0.75M | -1.5M 0.75M | -1.5M -0.375M | -2M 0.75M | -1M 0M | 1M -0.75M | 1M 0M |
Таблица 13
| bi | y1 | x2 | u1 | u2 | v1 | v2 | |
| x1 | 0.5 1.1 | 0.5 0.03333 | -0.25 0.1333 | 0.5 0.1667 | 0 0.1333 | -0.5 -0.03333 | 0 -0.1333 |
| y2 | 8.25 4.4 | 0.25 0.1333 | 1.875 0.5333 | 1.25 0.6667 | 1 0.5333 | -0.25 -0.1333 | -1 -0.5333 |
| w1 | 6.5 -5.5 | -0.5 -0.1667 | 1.25 -0.6667 | -0.5 -0.8333 | 0 -0.6667 | 0.5 0.1667 | 0 0.6667 |
| w2 | 5 -4.4 | 0 -0.1333 | 1 -0.5333 | 0 -0.6667 | 0 -0.5333 | 0 0.1333 | 0 0.5333 |
| Y' | 9.75M 8.25M | 0.75M 0.25M | -1.875M 1M | -1.25M 1.25M | -1M 1M | 0.25M -0.25M | 1M -1M |
| bi | y1 | y2 | u1 | u2 | v1 | v2 | |
| x1 | 1.6 | 0.5333 | 0.1333 | 0.6667 | 0.1333 | -0.5333 | -0.1333 |
| x2 | 4.4 | 0.1333 | 0.5333 | 0.6667 | 0.5333 | -0.1333 | -0.5333 |
| w1 | 1 | -0.6667 | -0.6667 | -1.333 | -0.6667 | 0.6667 | 0.6667 |
| w2 | 0.6 | -0.1333 | -0.5333 | -0.6667 | -0.5333 | 0.1333 | 0.5333 |
| Y' | 18M | 1M | 1M | 0M | 0M | 0M | 0M |
y1=y2=u1=u2=v1=v2=0
x1=1.6
x2=4.4
w1=1
w2=0.6
Проверим условие дополняющей нежёсткости:
xi*vi=0
ui*wi=0
Условия выполняются, следовательно, x1=1.6, x2=4.4 являются решением исходной задачи kвадратичного программирования. Координаты стационарной точки совпадают с координатами, полученных в качестве ответа. Стационарная точка удовлетворяет условиям ограничений.
Значение функции в точке (x1;x2) равно 0.
Ответ:
x1=1.6x2=4.4
f(x1;x2) = 0
Приложение 1
Для решения задачи #4 использована следующая программа на языке Си, скомпилированная gcc (GCC) 4.0.0 20050519 (Red Hat 4.0.0-8). Её текст приведён ниже:#include <stdio.h>
#define x 7
#define y 5
double mc[x*y] =
{
1, 2, -0.5, 1, 0, -1, 0,
8, -0.5, 2, 1, 1, 0, -1,
7, 1, 1, 0, 0, 0, 0,
5, 0, 1, 0, 0, 0, 0,
9, -1.5, -1.5, -2, -1, 1, 1
};
double mt[x*y];
void mprint (double* m, int xs, int ys)
{
int i, j;
printf ("\n");
for (j = 0; j < ys; j++)
{
for (i = 0; i < xs; i++)
{
printf ("%10.4lg ", m[j*xs+i]);
}
printf ("\n");
}
}
int main (void)
{
int i, j, i1, j1, it, jt;
double msx, msx1;
// Выбираем разрешающий эл-т
nextmtx:
printf ("\nИсходная матрица коэффициентов:"); mprint (mc, x, y);
getch ();
msx = 10000.;
for (i = 0; i < x; i++)
{
if (mc[(y-1)*x+i] < 0)
{
// Возможно, найден разрешающий столбец
for (j = 0; j < y; j++)
{
// Ищем наименьшее отношение своб. члена к эл-ту разр. столбца
if (mc[j*x+i] < 1e-32)
continue; // Нулевой или отрицательный
msx1 = mc[j*x] / mc[j*x+i];
if (msx > msx1) // Частное св.ч / р.эл
{
msx = msx1; // наименьшее ищем
it = i; jt = j; // координаты р.эл.
}
}
if (msx > 9999.) continue; // Нет положительных эл-тов
else // найден р.эл., mx != 0
{
i = it; j = jt; // его координаты
}
printf ("\n Разрешающий элемент: a(%d;%d) = %lg", j+1, i+1, mc[j*x+i]);
if (mc[j*x+i] > 0)
{
// Это и есть разрешающий элемент (s_el), находим обратную величину
mt[j*x+i] = 1. / mc[j*x+i];
for (i1 = 0; i1 < x; i1++)
{
// Разрешающая строка ( 1/s_el)
if (i1 == i) continue; // Пропустить сам s_el
mt[j*x+i1] = mt[j*x+i] * mc[j*x+i1];
}
for (j1 = 0; j1 < y; j1++)
{
// Разрешающий столбец (-1/s_el)
if (j1 == j) continue; // Пропустить сам s_el
mt[j1*x+i] = - mt[j*x+i] * mc[j1*x+i];
}
// успешно составлены разр. строка и столбец.
// теперь составляем остальные коэфф-ты
for (j1 = 0; j1 < y; j1++)
{
if (j1 == j) continue; // Пропустить всю разреш. строку
for (i1 = 0; i1 < x; i1++)
{
if (i1 == i) continue; // И столбец тоже
// Произведение нижней части столбца
// на верхнюю часть строки
mt[j1*x+i1] = mt[j1*x+i] * mc[j*x+i1];
}
}
/*
* Всё. Готова матрица нижних значений, теперь нужно
* поместить всё на свои места в mc
*/
printf ("\nМатрица нижних значений:"); mprint (mt, x, y);
getch ();
for (j1 = 0; j1 < y; j1++)
{
for (i1 = 0; i1 < x; i1++)
{
if ((j1 == j) || (i1 == i))
{
/*
* Разрешающая строка или столбец
* просто ложим элементы в mc
*/
mc[j1*x+i1] = mt[j1*x+i1];
}
else
// иначе - сумму
mc[j1*x+i1] += mt[j1*x+i1];
}
}
// Всё готово к очередному шагу.
goto nextmtx; // след. матрица
}
// Этот эл-т не подходит, т.к. он отрицательный
}
// Если так и не было подходящего эл-та, то проверяем след. столбец
}
// отрицательны коэфф-тов при целевой ф-ции не найдено, следовательно, решение оптимально
printf ("\nОптимизировано. Ответ:"); mprint (mc, x, y);
return 0;
}
Программа компилировалась командной строкой:
gcc simplex.c -o simplex
, запускалась:
./simplex
и выдавала на консоль пошаговое решение задачи, которое было занесено в симплекс-таблицы (см. табл. 12-14) четвёртой задачи данной курсовой работы.
Список использованной литературы
1. Кремер Н. Ш., Путко Б. А., Трощин И. М. «Исследование операций в экономике» - М.: ЮНИТИ, 2004. - 407 с.2. Плотникова Н. В. Курс лекций (ПС)