Контрольная работа на тему Статистические методы в экономике
Работа добавлена на сайт bukvasha.net: 2014-11-18Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Задача 1
Провести структурно-аналитическую группировку 20 регионов страны (см. табл.3) по двум признакам-факторам, положив в основание группировки нижеуказанный для конкретного варианта признак. Рассчитайте среднее значение группировочного признака по каждой группе. Результаты отобразить в статистической таблице, оформленной в соответствии с установленными правилами.
Постройте графически полученный ряд распределения признака в виде гистограммы.
По результатам группировки определите:
- показатели центра распределения: средние арифметическое значение группировочного признака моду и медиану;
- показатели вариации признака:
- абсолютные показатели: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия.
- относительные показатели: коэффициенты осцилляции, вариации и линейной вариации;
- сделайте вывод о форме распределения на основании расчета коэффициентов асимметрии и эксцесса.
По результатам расчетов сделать вывод.
Таблица 1
Выбор группировочного признака осуществляется по следующей схеме, представленной в таблице 2.
Таблица 2
РЕШЕНИЕ
Группировка - это разбиение совокупности на группы, однородные по какому-либо признаку. Метод группировок основывается на 2-х категориях: группировочный признак и интервал. Группировочный признак - это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы. Интервал - очерчивает количественные границы групп.
Величину интервала в данной задаче можно определить следующим образом:

(1)
х max, x min - максимальное и минимальное значение варьирующего признака. Для нахождения числа групп служит формула Стерджесса:

(2)
1. Сначала определим количество групп (2):
где N - количество элементов совокупности. N =20

=5,32, значит групп 5
1. Определим длину интервала по формуле (1):

=7,76 млн.руб.
Величина интервала 7,76 млн.руб.
35,0 – 42,76; 42,76-50,52; 50,52 – 58,28; 58,28 – 66,04; 66,04 – 73,8
Таблица 4
При построении вариационного ряда все расчеты отражаем в таблице.
Таблица 5
Средняя величина - выражает величину признака, отнесенную к единице совокупности.
- средняя арифметическая взвешенная

- средняя арифметическая простая

где Xi - варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
n- число наблюдение;
fi - частота, показывающая, сколько раз встречается i-e значение осредняемого признака.

Показатели вариации:
- размах вариации:
 ,
,
где хmax - максимальное значение признака,
х min – минимальное значение признака;
R=73,8-35,0=38,8
- среднее линейное отклонение:
-  ,
,
где  – индивидуальные значения признака,
– индивидуальные значения признака,
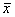 – средняя величина,
– средняя величина,
f– частота;
d=272-540,12=268,12
- дисперсия:
 ;
;

- среднее квадратическое отклонение:
 ;
;

- коэффициент вариации:
 .
.

Коэффициент вариации показывает степень однородности совокупности. Так как V > 33% - совокупность неоднородна.
- коэффициент осцилляции:

V=38,8/540,12*100%=7,18
- линейный коэффициент вариации:

V=268,12/540,12*100%=49,64
2. Производим группировку по второму признаку: Валовые инвестиции, млн.руб.
Величина интервала:
h= у max - у min /число групп
у max, у min - максимальное и минимальное значение варьирующего признака
Для нахождения числа групп служит формула Стерджесса

1. Сначала определим количество групп:
где N - количество элементов совокупности. N =20

=5,32,
значит групп 5
1. Определим длину интервала по формуле (1):
h=13,3-6,3/5=1,4 млн.руб.
Величина интервала 1,4 млн.руб.
6,3 – 7,7; 7,7-9,1; 9,1 – 10,5; 10,5 – 11,9; 11,9 – 13,3
Таблица 6
При построении вариационного ряда все расчеты отражаем в таблице.
Таблица 7
Средняя величина - выражает величину признака, отнесенную к единице совокупности.
- средняя арифметическая взвешенная

- средняя арифметическая простая

где Уi - варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
n- число наблюдение;
fi - частота, показывающая, сколько раз встречается i-e значение осредняемого признака.

Показатели вариации:
- размах вариации:
R=ymax-ymin
где уmax - максимальное значение признака,
у min – минимальное значение признака;
R=13,3-6,3=7,0
- среднее линейное отклонение:
 ,
,
где у – индивидуальные значения признака,
у – средняя величина,
f– частота;
d=9,86-9,92=0,06
- дисперсия:
 ;
;

- среднее квадратическое отклонение:
 ;
;

- коэффициент вариации:
 .
.

Коэффициент вариации показывает степень однородности совокупности. Так как V < 33% - совокупность однородна.
- коэффициент осцилляции:

V=7,0/9,92*100%=70,56
- линейный коэффициент вариации:

V=0,06/9,92*100%=0,06%
Задача 2
Разделив первые 30 регионов (см. данные из Задания 1) на 2 группы по величине признака, соответствующего вашему варианту, проверьте правило сложения дисперсий.
По результатам расчетов сделать вывод.
Методика решения
Межгрупповая дисперсия  характеризует систематическую вариацию результативного порядка, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних
характеризует систематическую вариацию результативного порядка, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних  , от общей средней
, от общей средней 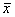 :
:
 ,
,
где f — численность единиц в группе.
Внутригрупповая (частная) дисперсия  отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы
отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы  , (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
, (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
 ;
;
 .
.
На основании внутригрупповой дисперсии по каждой группе, т.е. на основании  можно определить среднюю из внутригрупповых дисперсий:
можно определить среднюю из внутригрупповых дисперсий:

Согласно правилу сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

Ход расчета дисперсий:
1)определяем значения дисперсий по каждой группе (внутригрупповые дисперсии);
 у2=У(y-yi)2f/ Уf
у2=У(y-yi)2f/ Уf
у1 2=5024830,6/6=837471,76 у1 2=51/6=8,5
у2 2=4870450,2/2=2435225,1 у2 2=4,62/2=2,31
у3 2=4718478,2/2=2359239,1 у3 2=2,5/2=1,25
у4 2=4568915,2/7=652702,17 у4 2=8,2/5=1,64
у5 2=4421760,8/3=1473920,2 у5 2=35,9/5=7,18
2) среднее значение дисперсии по двум группам;

у12 2=1180222\20=5901,1 у12 2=102,22\20=5,11
3) общую дисперсию по правилу сложения.

у2=5906,211/20=295,31
Для проверки результатов расчета рассчитываем общую дисперсию, без учета деления регионов на группы.
Задача 3
По группе регионов (см. исходные данные Задания №1) необходимо:
1) найти линейное уравнение парной регрессии между результативным (ВРП) и факторным признаком (хi) , оценить полученные результаты;
х1 – потребительские расходы;
х2 – государственные расходы
х3 – валовые инвестиции
х4 – экспорт
х5 – средняя заработная плата
2) количественно оценить тесноту связи между результативным признаком и факторами.
3) по исходным данным постройте эмпирическую и теоретическую линии регрессии.
4) проверить адекватность модели на основе критерия Фишера и значимость коэффициентов регрессии на основе критерия Стьюдента.
По результатам расчетов сделать вывод.
Таблица 7 Варианты заданий
РЕШЕНИЕ
Параметры уравнения парной линейной зависимости а и b

могут быть определены методом наименьших квадратов путем решения системы нормальных уравнений:

Параметр b - это линейный коэффициент регрессии, характеризующий направление (+b - связь прямая; - b - связь обратная) и силу связи.
Он может быть рассчитан по формуле:

b=60,6 272
b=16483,2 - 332,6/295,31=54,69
Коэффициент регрессии применяют для определения коэффициента эластичности, который показывает, на сколько процентов изменится величина результативного признака у при изменении признака-фактора х на один процент. Для определения коэффициента эластичности используется формула:

Э=54,69*272/60,6=245,47
Подставляя эмпирические значения признака фактора х в уравнение регрессии, определим теоретические значения результативного признака уx. попуществляется по формулеа, а значимость коэффициентов регрессии на основе критерия Стьюдента
Провести структурно-аналитическую группировку 20 регионов страны (см. табл.3) по двум признакам-факторам, положив в основание группировки нижеуказанный для конкретного варианта признак. Рассчитайте среднее значение группировочного признака по каждой группе. Результаты отобразить в статистической таблице, оформленной в соответствии с установленными правилами.
Постройте графически полученный ряд распределения признака в виде гистограммы.
По результатам группировки определите:
- показатели центра распределения: средние арифметическое значение группировочного признака моду и медиану;
- показатели вариации признака:
- абсолютные показатели: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия.
- относительные показатели: коэффициенты осцилляции, вариации и линейной вариации;
- сделайте вывод о форме распределения на основании расчета коэффициентов асимметрии и эксцесса.
По результатам расчетов сделать вывод.
Таблица 1
| Вариант | Регион |
| 3 | с 10 по 29 |
Таблица 2
| Вариант | Группировочный признак |
| с 1 по 4 | «ВРП» |
Исходные данные
Таблица 3
| Регион | ВВП, млн.руб. | Потребительские расходы, млн.руб. | Государственные расходы, млн.руб. | Валовые инвестиции, млн.руб. | Экспорт, млн.руб. | Средняя зп, руб. |
| 10 | 36,6 | 18,3 | 3,7 | 6,6 | 8,4 | 2150 |
| 11 | 39,2 | 19,6 | 3,9 | 7,1 | 9,0 | 2300 |
| 12 | 41,8 | 20,9 | 4,2 | 7,5 | 9,6 | 2450 |
| 13 | 44,4 | 22,2 | 4,4 | 8,0 | 10,2 | 2600 |
| 14 | 66,0 | 33,0 | 6,6 | 11,9 | 15,2 | 2750 |
| 15 | 68,6 | 34,3 | 6,9 | 12,3 | 15,8 | 2900 |
| 16 | 71,2 | 35,6 | 7,1 | 12,8 | 16,4 | 3050 |
| 17 | 73,8 | 36,9 | 7,4 | 13,3 | 17,0 | 1900 |
| 18 | 35,0 | 17,5 | 3,5 | 6,3 | 8,1 | 2050 |
| 19 | 37,6 | 18,8 | 3,8 | 6,8 | 8,6 | 2200 |
| 20 | 40,2 | 20,1 | 4,0 | 7,2 | 9,2 | 2350 |
| 21 | 42,8 | 21,4 | 4,3 | 7,7 | 9,8 | 2500 |
| 22 | 55,0 | 27,5 | 5,5 | 9,9 | 12,7 | 2650 |
| 23 | 57,6 | 28,8 | 5,8 | 10,4 | 13,2 | 2360 |
| 24 | 60,2 | 30,1 | 6,0 | 10,8 | 13,8 | 2510 |
| 25 | 60,0 | 30,0 | 6,0 | 10,8 | 13,8 | 2660 |
| 26 | 62,6 | 31,3 | 6,3 | 11,3 | 14,4 | 2810 |
| 27 | 65,2 | 32,6 | 6,5 | 11,7 | 15,0 | 2960 |
| 28 | 67,8 | 33,9 | 6,8 | 12,2 | 15,6 | 2000 |
| 29 | 70,4 | 35,2 | 7,0 | 12,7 | 16,2 | 2150 |
Группировка - это разбиение совокупности на группы, однородные по какому-либо признаку. Метод группировок основывается на 2-х категориях: группировочный признак и интервал. Группировочный признак - это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы. Интервал - очерчивает количественные границы групп.
Величину интервала в данной задаче можно определить следующим образом:

х max, x min - максимальное и минимальное значение варьирующего признака. Для нахождения числа групп служит формула Стерджесса:
1. Сначала определим количество групп (2):
где N - количество элементов совокупности. N =20
1. Определим длину интервала по формуле (1):
Величина интервала 7,76 млн.руб.
35,0 – 42,76; 42,76-50,52; 50,52 – 58,28; 58,28 – 66,04; 66,04 – 73,8
Таблица 4
| № группы | Группировка по ВВП | № региона | ВВП, млн.руб. |
| I | 35,0 – 42,76 | 18 | 35,0 |
| 10 | 36,6 | ||
| 19 | 37,6 | ||
| 11 | 39,2 | ||
| 20 | 40,2 | ||
| 12 | 41,8 | ||
| II | 42,76-50,52 | 21 | 42,8 |
| 13 | 44,4 | ||
| III | 50,52 – 58,28 | 22 | 55,0 |
| 23 | 57,6 | ||
| IV | 58,28 – 66,04 | 14 | 66,0 |
| 27 | 65,2 | ||
| 25 | 60,0 | ||
| 24 | 60,2 | ||
| 26 | 62,6 | ||
| 28 | 67,8 | ||
| 15 | 68,6 | ||
| V | 66,04 – 73,8 | 16 | 71,2 |
| 17 | 73,8 | ||
| 29 | 70,4 |
Таблица 5
| Инвестиции в основные фонды | Число регионов, | Середина интервала, | | | |
| 35,0 – 42,76 | 6 | 38,88 | 233,28 | 251241,53 | 5024830,6 |
| 42,76-50,52 | 2 | 46,64 | 93,28 | 243522,51 | 4870450,2 |
| 50,52 – 58,28 | 2 | 54,4 | 108,8 | 235923,91 | 4718478,2 |
| 58,28 – 66,04 | 7 | 62,16 | 435,12 | 228445,76 | 4568915,2 |
| 66,04 – 73,8 | 3 | 69,92 | 209,76 | 221088,04 | 4421760,8 |
| Итого | 20 | 272 | 1080,24 | 1180222 | 23604435 |
- средняя арифметическая взвешенная
- средняя арифметическая простая
где Xi - варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
n- число наблюдение;
fi - частота, показывающая, сколько раз встречается i-e значение осредняемого признака.

Показатели вариации:
- размах вариации:
где хmax - максимальное значение признака,
х min – минимальное значение признака;
R=73,8-35,0=38,8
- среднее линейное отклонение:
-
где
f– частота;
d=272-540,12=268,12
- дисперсия:

- среднее квадратическое отклонение:
 ;
;
- коэффициент вариации:

Коэффициент вариации показывает степень однородности совокупности. Так как V > 33% - совокупность неоднородна.
- коэффициент осцилляции:
V=38,8/540,12*100%=7,18
- линейный коэффициент вариации:

V=268,12/540,12*100%=49,64
2. Производим группировку по второму признаку: Валовые инвестиции, млн.руб.
Величина интервала:
h= у max - у min /число групп
у max, у min - максимальное и минимальное значение варьирующего признака
Для нахождения числа групп служит формула Стерджесса
1. Сначала определим количество групп:
где N - количество элементов совокупности. N =20
значит групп 5
1. Определим длину интервала по формуле (1):
h=13,3-6,3/5=1,4 млн.руб.
Величина интервала 1,4 млн.руб.
6,3 – 7,7; 7,7-9,1; 9,1 – 10,5; 10,5 – 11,9; 11,9 – 13,3
Таблица 6
| № группы | Группировка по Валовым инвестициям, млн.руб | № региона | Валовые инвестиции, млн.руб |
| I | 6,3 – 7,7 | 12 | 7,5 |
| 18 | 6,3 | ||
| 10 | 6,6 | ||
| 19 | 6,8 | ||
| 11 | 7,1 | ||
| 20 | 7,2 | ||
| II | 7,7-9,1 | 21 | 7,7 |
| 13 | 8,0 | ||
| III | 9,1 – 10,5 | 22 | 9,9 |
| 23 | 10,4 | ||
| IV | 10,5 – 11,9 | 14 | 11,9 |
| 27 | 11,7 | ||
| 25 | 10,8 | ||
| 24 | 10,8 | ||
| 26 | 11,3 | ||
| V | 11,9 – 13,3 | 28 | 12,2 |
| 16 | 12,8 | ||
| 17 | 13,3 | ||
| 29 | 12,7 | ||
| 15 | 12,3 |
Таблица 7
| Валовые инвестиции, млн.руб | Число регионов, | Середина интервала, | | | |
| 6,3 – 7,7 | 6 | 7,0 | 43 | 8,5264 | 51 |
| 7,7-9,1 | 2 | 8,4 | 16,8 | 2,31 | 4,62 |
| 9,1 – 10,5 | 2 | 8,8 | 19,6 | 1,2544 | 2,5 |
| 10,5 – 11,9 | 5 | 11,2 | 56 | 1,6384 | 8,2 |
| 11,9 – 13,3 | 5 | 12,6 | 63 | 7,1824 | 35,9 |
| Итого | 20 | 60,6 | 198,4 | 20,9116 | 102,22 |
- средняя арифметическая взвешенная
- средняя арифметическая простая
где Уi - варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
n- число наблюдение;
fi - частота, показывающая, сколько раз встречается i-e значение осредняемого признака.

Показатели вариации:
- размах вариации:
R=ymax-ymin
где уmax - максимальное значение признака,
у min – минимальное значение признака;
R=13,3-6,3=7,0
- среднее линейное отклонение:
где у – индивидуальные значения признака,
у – средняя величина,
f– частота;
d=9,86-9,92=0,06
- дисперсия:

- среднее квадратическое отклонение:
 ;
;- коэффициент вариации:
Коэффициент вариации показывает степень однородности совокупности. Так как V < 33% - совокупность однородна.
- коэффициент осцилляции:
V=7,0/9,92*100%=70,56
- линейный коэффициент вариации:

V=0,06/9,92*100%=0,06%
Задача 2
Разделив первые 30 регионов (см. данные из Задания 1) на 2 группы по величине признака, соответствующего вашему варианту, проверьте правило сложения дисперсий.
По результатам расчетов сделать вывод.
Методика решения
Межгрупповая дисперсия
где f — численность единиц в группе.
Внутригрупповая (частная) дисперсия
На основании внутригрупповой дисперсии по каждой группе, т.е. на основании

Согласно правилу сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:
Ход расчета дисперсий:
1)определяем значения дисперсий по каждой группе (внутригрупповые дисперсии);
у1 2=5024830,6/6=837471,76 у1 2=51/6=8,5
у2 2=4870450,2/2=2435225,1 у2 2=4,62/2=2,31
у3 2=4718478,2/2=2359239,1 у3 2=2,5/2=1,25
у4 2=4568915,2/7=652702,17 у4 2=8,2/5=1,64
у5 2=4421760,8/3=1473920,2 у5 2=35,9/5=7,18
2) среднее значение дисперсии по двум группам;
у12 2=1180222\20=5901,1 у12 2=102,22\20=5,11
3) общую дисперсию по правилу сложения.

у2=5906,211/20=295,31
Для проверки результатов расчета рассчитываем общую дисперсию, без учета деления регионов на группы.
Задача 3
По группе регионов (см. исходные данные Задания №1) необходимо:
1) найти линейное уравнение парной регрессии между результативным (ВРП) и факторным признаком (хi) , оценить полученные результаты;
х1 – потребительские расходы;
х2 – государственные расходы
х3 – валовые инвестиции
х4 – экспорт
х5 – средняя заработная плата
2) количественно оценить тесноту связи между результативным признаком и факторами.
3) по исходным данным постройте эмпирическую и теоретическую линии регрессии.
4) проверить адекватность модели на основе критерия Фишера и значимость коэффициентов регрессии на основе критерия Стьюдента.
По результатам расчетов сделать вывод.
Таблица 7 Варианты заданий
| Номер варианта | Регион | xi | Номер варианта | Регион | xi | Номер варианта | Регион | xi |
| 1 | с 1 по 20 | Х1 | 11 | с 50 по 69 | Х1 | 21 | с 32 по 51 | Х1 |
| 2 | с 5 по 24 | Х2 | 12 | с 55 по 74 | Х2 | 22 | с 28 по 47 | Х2 |
| 3 | с 10 по 29 | Х3 | 13 | с 60 по 79 | Х3 | 23 | с 81 по 100 | Х3 |
| 4 | с 15 по 34 | Х4 | 14 | с 65 по 84 | Х4 | 24 | с 76 по 95 | Х4 |
| 5 | с 20 по 39 | Х5 | 15 | с 70 по 89 | Х5 | 25 | с 61 по 80 | Х5 |
| 6 | с 25 по 44 | Х1 | 16 | с 75 по 94 | Х1 | 26 | с 51 по 70 | Х1 |
| 7 | с 30 по 49 | Х2 | 17 | с 80 по 99 | Х2 | 27 | с 41 по 60 | Х2 |
| 8 | с 35 по 54 | Х3 | 18 | с 14 по 33 | Х3 | 28 | с 21 по 40 | Х3 |
| 9 | с 40 по 59 | Х4 | 19 | с 17 по 36 | Х4 | 29 | с 3 по 22 | Х4 |
| 10 | с 45 по 64 | Х5 | 20 | с 23 по 42 | Х5 | 30 | с 54 по 73 | Х5 |
Параметры уравнения парной линейной зависимости а и b

Параметр b - это линейный коэффициент регрессии, характеризующий направление (+b - связь прямая; - b - связь обратная) и силу связи.
Он может быть рассчитан по формуле:
b=60,6 272
b=16483,2 - 332,6/295,31=54,69
Коэффициент регрессии применяют для определения коэффициента эластичности, который показывает, на сколько процентов изменится величина результативного признака у при изменении признака-фактора х на один процент. Для определения коэффициента эластичности используется формула:
Э=54,69*272/60,6=245,47
Подставляя эмпирические значения признака фактора х в уравнение регрессии, определим теоретические значения результативного признака уx. попуществляется по формулеа, а значимость коэффициентов регрессии на основе критерия Стьюдента
Тесноту связи так же необходимо охарактеризовать линейным коэффициентом корреляции.

или


Задача 4
По предприятию имеются следующие данные о реализованной продукции, определите:
- индивидуальные индексы цены, физического объема и товарооборота;
- агрегатный индекс товарооборота, цен и физического объема (показать их взаимосвязь)
- абсолютное изменение товарооборота за счет изменения ассортимента продукции и цены продажи;
- индекс структурных сдвигов, индексы фиксированного и переменного состава, показать их взаимосвязь.
По результатам расчетов сделать вывод.
Значение N определяется по последней цифре номера зачетной книжки студента. N=3
Таблица 9 Исходные данные
РЕШЕНИЕ
Значение N определяется по последней цифре номера зачетной книжки студента. N=3
Таблица 10 Исходные данные
Таблица 11 Исходные данные
Схема расчета индивидуального индекса:

,
где к1 – индексируемый показатель в отчетном периоде,
ко– индексируемый показатель в базисном периоде.
Агрегатный индекс товарооборота:


Агрегатный индекс цены:


Агрегатный индекс физического объема:


Индекс переменного состава =


Индекс постоянного состава =

=0,047
Индекс структурных сдвигов =


Задача 5
Из общего количества рабочих предприятия была проведена Х %-я случайная бесповторная выборка с целью определения затрат времени на проезд к месту работы. Результаты выборки представлены в таблице 6 .
Таблица 10
Определите:
- доверительный интервал средних затрат времени на проезд к месту, гарантируя результат с вероятностью 0,997;
- долю рабочих предприятия, у которых затраты времени на проезд к месту работы составляют 60 мин. и более, гарантируя результат с вероятностью 0,954
Таблица 11
РЕШЕНИЕ
Границы генеральной средней определяются как:

,
где 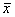
- генеральная средняя,

- выборочная средняя,
Д 
- предельная ошибка выборочной средней:
- при случайной бесповторной выборке:
 ,
,
где 
- коэффициент доверия, зависящий от того, с какой вероятностью определяется предельная ошибка:
при р=0,663 t=1,
при р=0,954 t=2,
при p= 0,997 t=3;
n – объем выборочной совокупности,
N – объем генеральной совокупности,

- дисперсия признака выборочной совокупности.
Дx=2 

Границы генеральной доли находятся как:

,
где р – генеральная доля,

- выборочная доля (доля рабочих, обладающих указанным признаком):

,
где 
- число единиц, обладающих данным признаком,
n - объем выборочной совокупности.


- предельная ошибка доли:
 .
.

=0,758
2. Елисеева И.И., Флуд Н.А., Юзбашев М.М. Практикум по общей теории статистики: Учеб. пособие.- М.: Финансы и статистика,2008.- 512с.
3. Общая теория статистики: Учебник./ Под.ред. И.И. Елисеевой. - 5-е изд., перераб. и доп.- М.: Финансы и статистика, 2008.- 656с.
4. Практикум по теории статистики: Учеб. пособие/ Под.ред. Шмойловой Р.А. - 3-е изд..– М.: Финансы и статистика,2008.-416с.
5. Салин В.Н., Чурилова Э.Ю. Курс теории статистики для подготовки специалистов финансово-экономического профиля: Учебник. – М.: Финансы и статистика, 2007. – 480с.
6. Статистика: Учебник / И.И. Елисеева, И.И. Егорова и др.; Под ред. проф. И.И. Елисеевой. – М.: ТК Велби, Изд-во Проспект, 2004
7. Теория статистики: Учебник/ Под.ред. Шмойловой Р.А. - 5-е изд..– М.: Финансы и статистика,2008.- 656с.
8. Материалы сайта Государственного комитета РФ по статистике



Задача 4
По предприятию имеются следующие данные о реализованной продукции, определите:
- индивидуальные индексы цены, физического объема и товарооборота;
- агрегатный индекс товарооборота, цен и физического объема (показать их взаимосвязь)
- абсолютное изменение товарооборота за счет изменения ассортимента продукции и цены продажи;
- индекс структурных сдвигов, индексы фиксированного и переменного состава, показать их взаимосвязь.
По результатам расчетов сделать вывод.
Значение N определяется по последней цифре номера зачетной книжки студента. N=3
Таблица 9 Исходные данные
| Продукция | Продано продукции, кг. | Цена 1 кг. | ||
| Базисный период | Текущий период | Базисный период | Текущий период | |
| Кирпич | 1000+10*N | 800+10*N | 45+N | 50+N |
| Шифер | 900+10*N | 960+10*N | 51+N | 48+N |
| Черепица | 800+10*N | 830+10*N | 52+N | 54+N |
| Металл листовой | 300+10*N | 520+10*N | 58+N | 60+N |
Значение N определяется по последней цифре номера зачетной книжки студента. N=3
Таблица 10 Исходные данные
| Продукция | Продано продукции, кг. | Цена 1 кг. | ||
| Базисный период | Текущий период | Базисный период | Текущий период | |
| Кирпич | 1000+10*3 | 800+10*3 | 45+3 | 50+3 |
| Шифер | 900+10*3 | 960+10*3 | 51+3 | 48+3 |
| Черепица | 800+10*3 | 830+10*3 | 52+3 | 54+3 |
| Металл листовой | 300+10*3 | 520+10*3 | 58+3 | 60+3 |
| Продукция | Продано продукции, кг. | Цена 1 кг. | ||
| Базисный период | Текущий период | Базисный период | Текущий период | |
| Кирпич | 1030 | 830 | 48 | 53 |
| Шифер | 930 | 990 | 54 | 51 |
| Черепица | 830 | 860 | 55 | 57 |
| Металл листовой | 330 | 550 | 61 | 63 |
где к1 – индексируемый показатель в отчетном периоде,
ко– индексируемый показатель в базисном периоде.
Агрегатный индекс товарооборота:
Агрегатный индекс цены:
Агрегатный индекс физического объема:
Индекс переменного состава =
Индекс постоянного состава =
Индекс структурных сдвигов =
Задача 5
Из общего количества рабочих предприятия была проведена Х %-я случайная бесповторная выборка с целью определения затрат времени на проезд к месту работы. Результаты выборки представлены в таблице 6 .
Таблица 10
| Затраты времени на проезд к месту работы, мин | До 30 | 30-40 | 40-50 | 50-60 | 60-70 |
| Число рабочих | А | 80 | В | 55 | С |
- доверительный интервал средних затрат времени на проезд к месту, гарантируя результат с вероятностью 0,997;
- долю рабочих предприятия, у которых затраты времени на проезд к месту работы составляют 60 мин. и более, гарантируя результат с вероятностью 0,954
Таблица 11
| Вариант | А | В | С | Х | Вариант | А | В | С | Х |
| 1 | 70 | 200 | 45 | 30 | 16 | 90 | 222 | 47 | 10 |
| 2 | 80 | 210 | 45 | 15 | 17 | 75 | 225 | 49 | 20 |
| 3 | 90 | 222 | 46 | 10 | 18 | 77 | 230 | 50 | 35 |
| 4 | 75 | 225 | 47 | 20 | 19 | 79 | 214 | 51 | 5 |
| 5 | 77 | 230 | 49 | 35 | 20 | 73 | 263 | 52 | 30 |
| 6 | 79 | 214 | 50 | 5 | 21 | 70 | 210 | 45 | 15 |
| 7 | 73 | 263 | 51 | 25 | 22 | 80 | 199 | 43 | 10 |
| 8 | 71 | 210 | 52 | 30 | 23 | 90 | 250 | 46 | 20 |
| 9 | 70 | 199 | 45 | 15 | 24 | 75 | 231 | 47 | 35 |
| 10 | 80 | 250 | 43 | 10 | 25 | 77 | 222 | 49 | 5 |
| 11 | 90 | 231 | 40 | 20 | 26 | 79 | 233 | 50 | 25 |
| 12 | 75 | 222 | 45 | 35 | 27 | 73 | 200 | 51 | 30 |
| 13 | 77 | 233 | 45 | 5 | 28 | 90 | 250 | 52 | 15 |
| 14 | 70 | 200 | 45 | 30 | 29 | 75 | 231 | 45 | 10 |
| 15 | 80 | 210 | 46 | 15 | 30 | 77 | 222 | 43 | 20 |
Границы генеральной средней определяются как:
где
Д
- при случайной бесповторной выборке:
 ,
, где
при р=0,663 t=1,
при р=0,954 t=2,
при p= 0,997 t=3;
n – объем выборочной совокупности,
N – объем генеральной совокупности,
Дx=2
Границы генеральной доли находятся как:
где р – генеральная доля,

где
n - объем выборочной совокупности.

 .
. СПИСОК ЛИТЕРАТУРЫ
1. Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики: Учеб. пособие.- 2-е изд. перераб. и доп.- М.: Финансы и статистика, 2003.-336с.
2. Елисеева И.И., Флуд Н.А., Юзбашев М.М. Практикум по общей теории статистики: Учеб. пособие.- М.: Финансы и статистика,2008.- 512с.
3. Общая теория статистики: Учебник./ Под.ред. И.И. Елисеевой. - 5-е изд., перераб. и доп.- М.: Финансы и статистика, 2008.- 656с.
4. Практикум по теории статистики: Учеб. пособие/ Под.ред. Шмойловой Р.А. - 3-е изд..– М.: Финансы и статистика,2008.-416с.
5. Салин В.Н., Чурилова Э.Ю. Курс теории статистики для подготовки специалистов финансово-экономического профиля: Учебник. – М.: Финансы и статистика, 2007. – 480с.
6. Статистика: Учебник / И.И. Елисеева, И.И. Егорова и др.; Под ред. проф. И.И. Елисеевой. – М.: ТК Велби, Изд-во Проспект, 2004
7. Теория статистики: Учебник/ Под.ред. Шмойловой Р.А. - 5-е изд..– М.: Финансы и статистика,2008.- 656с.
8. Материалы сайта Государственного комитета РФ по статистике