1.2 Історичний корінь «Наочної концепції дробу»

Як показує історія становлення основних математичних понять, зокрема

поняття числа, дійсна необхідність у дробах виникла при вимірюванні величин за
допомогою обраної одиниці [8; 239]. «...Історично дроби виникли у зв'язку з потребою вимірювати». Вимірювання різних величин за допомогою обраних мір (одиниць) показувало людям, що вираження його результату цілими числами найчастіше носить наближений характер. Для уточнення результатів вимірювання необхідно було вибирати інші, менші одиниці, які мали певне відношення до колишнього. «Таким чином, практика привела людину до необхідності використання різних одиниць, а з відношень одиниць цих конкретних мір виникло абстрактне поняття дробу» [8; 240].
Дробові числа широко застосовувалися древніми єгиптянами, вавилонянами, індусами, потім греками, а в середньовіччя - арабами. При цьому є підстави думати, що й у математиці як науці дроби спочатку розглядалися у зв'язку із задачами виміру величин. Так, стародавні греки раціональний дріб виду  навіть не називали числом - це було для них відношення, розгляд якого поклало початок теорії звичайних дробів [8; 243]. Виклад звичайних дробів, даний Симоном Стевином наприкінці XVI в., супроводжувався виданням праці того ж автора про десяткові дроби [8; 245], які традиційно пов'язані з потребами саме вимірювання. Разом з тим уже з XIIст. у працях по арифметиці при описі ділення чисел з остачею дроби розглядаються як частини чисел (ця точка зору може бути вловлена ще в єгиптян) [8; 255].
Аж до ХVП-ХVПІст. у математиці вироблялися самі правила дій із дробовими числами. У підручники європейських шкіл викладання дробів стало проникати в XVIIIст. При цьому Хр. Вольф у своєму керівництві вперше висловлює вимогу про те, щоб закони арифметичних дій, раніше встановлені при обігу із цілими числами, обґрунтовувалися й для дробів. Але методи цього обґрунтування були розроблені тільки в XIX в. [8; 245-263].
Практика дій із самими дробами, вірніше з їх символами, наприклад з вираженням відношення , поступово приводила до того, що усередині математики форма цих «нових» чисел усе більше й більше відділялась від їхньої першооснови, від вимірювання. «Останній, і самий істотний, крок, - пишуть

Р. Курант і Г. Роббінс, торкаючись цього питання, - був зроблений уже усвідомлено, після багатьох сторіч нагромадження окремих зусиль: символ був звільнений від його конкретного зв'язку із процесом вимірювання й самих вимірюваних величин і став розглядатися як абстрактне число, самостійна сутність, зрівняна у своїх правах з натуральним числом».

Такий свідомий перехід до розгляду дробів як «самостійної сутності» був зроблений при розв‘язуванні особливих пізнавальних задач, пов‘язаних із внутрішнім розвитком самої математики як теоретичної дисципліни. Справа, в тому, що в межах тільки натуральних чисел не завжди здійсненні операції виділення й ділення. З розвитком математичного апарата виникає теоретична потреба в знятті цих обмежень. «Введення» дробових чисел усувало перешкоди, що заважають виконувати ділення (подібно тому як негативні числа усували перешкоди для виділення), але без порушення основних арифметичних законів (асоціативного, комутативного й дистрибутивного). Подібне розширення області чисел (тут - побудова системи раціональних чисел) є одним із проявів основного способу утворення нових понять у сучасній алгебрі [9; 8]. Це - «одна з форм характерного в математиці процесу узагальнення».
Ця форма узагальнення й відповідний їй алгебраїчний спосіб утворення нових понять був розроблений в XIXст. («принцип сталості формальних законів»). Потім в абстрактній формі цей спосіб розширення числової області застосовується в теорії пар, що використається, зокрема, і для введення дробових чисел. Якщо операція над двома числами неможлива в області наявних чисел, то вводиться новий символ у вигляді пари колишніх чисел (а,в, для якої встановлюються визначення рівності, більше, менше й т.д. Якщо арифметичні дії над новими символами підкоряються законам дій над колишніми, тонові символи визнаються числами [8; 264].
Теорія пар прийнята в сучасній математиці, дозволяє логічно бездоганно будувати числові системи без якого-небудь звертання до «конкретної дійсності», у випадку раціональних чисел - без звертання до вимірювання. Вона стала потужним знаряддям теоретичного дослідження й, природно, уважається єдино й справді науковою.
Ця установка в теорії числових систем поступово стала проникати й поширюватися на викладання математики як у вищих, так й у середніх навчальних закладах. Цілком природне прагнення педагогів до відновлення курсу математики приводило до того, що зазначений підхід до введення чисел став сприйматися як єдино сучасний і строгий. Створилася ситуація, що ще в 30-і роки була в такий спосіб охарактеризована А. Н. Колмогоровим: «...Дуже поширена думка, що найбільш «науковим» підходом до введення раціональних чисел є підхід з боку довільного розширення області цілих чисел для досягнення необмеженої реалізації дії ділення... Часто учням повідомляють помилкові твердження, що справді наукова побудова раціональних чисел не повинна мати нічого загального з вимірюванням величин. Часто говорять, що правила дії над дробами є лише «зручні угоди», що зберігають незмінними закони дій» [9; 8-9].
Однак зазначена думка, розповсюджена серед методистів, послужила причиною того положення речей, коли вимірювання величин як джерело дробів стало ігноруватися. Це відношення до реального вимірювання було б, видимо, правомірним, якби традиційний зміст шкільної математики змінився б настільки, що злився б з поняттями абстрактної алгебри як навчанні про операції. Але тоді, звичайно, це був би інший навчальний предмет, з іншими загальними освітніми цілями, у якому, до речі, різні види чисел мали б й іншу пізнавальну цінність, чим у нинішньому навчальному предметі. Однак так далеко ні в недалекому минулому, ні в найближчому майбутньому перебудова курсу не зайшла й не зайде. Цей курс усе ще далекий від способів утворення понять у загальній (абстрактній) алгебрі, що у свій час саме й було відзначено А. Н. Колмогоровим: «Вся ця концепція занадто абстрактна не тільки для того, щоб у явному вигляді викладатися в середній школі, але й для того, щоб служити опорою для вчителя в цьому викладанні». І потім він констатує справжнє положення речей: «У дійсності, звичайно, ніхто й не намагається викладати в школі ідеї сучасної абстрактної алгебри» [ 9; 9].
Іншими словами, хоча ідеї абстрактної алгебри в школі й не викладаються, однак їхній непрямий вплив на спосіб введення раціональних чисел у наявності. Варто мати на увазі, що такий вплив зовні виразився як негативно (ігнорування виміру), так і позитивно - через ідею про те, що одним із джерел дробів є ділення самих чисел. Оскільки ця дія загальноприйнята, а випадки ділення з остачею або при наявності діленого,, що менше дільника, часті, то в принципі неважко задачі такого ділення поставити у зв'язок з поняттям «числової пари», скористатися відсвітом алгебраїчного способу розширення числової області. Але саме його відсвітом, зовнішньою подібністю, а не суттю, що вимагає інших підстав, чим ті, які можуть бути поки дані в школі.
Таким чином, поряд з вимірюванням у методиці було зазначено ще одне і справді математичне джерело дробів - ділення чисел. Переважне положення цього джерела підкріплювалося ще тією загальною тенденцією, що властива всьому викладанню математики і яку А. Н. Колмогоров описав так: «...На різних щаблях навчання з різним ступенем сміливості незмінно проявляється та сама тенденція: можливо скоріше справитися із введенням чисел і далі вже говорити про числа й співвідношення між ними» [9; 10]. При наявності такої тенденції співвідношення цілих чисел, наявні в діленні, були, звичайно, зручною підставою для знайомства учнів із дробами.
Але тут необхідно було враховувати й фактори психологічного характеру. П'ятикласникам, а тим більше молодшим школярам, не можна задати в чисто знаковому, символічному плані принцип того ділення, що приводить до дробів. Потрібно було знайти його наочний корелят. У цій ролі й виступило так зване ділення самих речей, їхній поділ на частини, що у ході навчання може бути відносно легко пов‘язане з термінами, характерними для визначення звичайних дробів. Так цілком закономірно виникла «наочна концепція дробу», описана вище. Досить хитрими шляхами в історії викладання математики справжнє джерело утворення дробів - вимірювання - було замінено у дидактичних цілях сурогатом ділення чисел, так називаним «діленням речей». Подібна концепція одержала широкий резонанс не тільки в середніх навчальних закладах, а й у молодших класах, тим більше що тут немудро було зв'язати виділення «часток» з життєвим досвідом дитини в поділі предметів, наприклад у розламуванні яблук або розрізуванні кавунів.
1.3 Вимірювання величин як предметне джерело дробу
Чи зберігає вимірювання не тільки історичне, але й актуальне дидактичне значення при введенні дробів? Багато чого промовляє на користь позитивної відповіді на це питання. Так, розглянемо міркування, висловлені ще на початку століття найбільшим німецьким математиком Ф. Клейном, що спеціально зіставляв можливі шляхи введення дробів. Аналізуючи прийняту тоді в школі методику навчання дробам, він підкреслював той момент, що в порівнянні із цілими числами тут насамперед міняється субстрат наочних образів, якими інтерпретуються дробові числа, а саме «від кількості предметів ми переходимо до вимірювання, від предметів, що підлягають рахунку, ми переходимо до предметів, що підлягають вимірюванню».
Далі Ф. Клейн шкільну методику порівнює з «новою» постановкою питання, з «сучасним викладом», у якому на перший план виступає «формальна сторона справи» і загальні властивості дробу як «числової пари». У цій новій постановці, указує Ф. Клейн, ми «залишаємося цілком на ґрунті цілих чисел». Відомими передбачаються тільки цілі числа й дії над ними. Нові числа (дробові) визначаються як числові пари, а операції над ними - суть операції над цілими числами. Ніяких принципово нових «наочних подань» тут не дається, і вони не потрібні. На противагу цьому «шкільний же виклад істотно опирається на нове наочне подання про вимірювані величини, що дають безпосереднє інтуїтивне уявлення про дроби». Потім Ф. Клейн наводить гарний приклад, що пояснює розходження «шкільної» й «нової» постановки питання: «Уявимо собі істоту, що володіє тільки ідеєю про ціле число й зовсім не знає вимірювання. Для такої істоти шкільний виклад здавався б зовсім незрозумілим.
Яка із цих точок зору краще? «Нова точка зору, безсумнівно, чистіше, але в той же час і бідніше», - відзначає Ф. Клейн. Вона дає тільки абстрактне, логічно точне введення дробів, але залишає відкритим не менш важливе питання: чи застосовна ця теоретична побудова «до вимірюваних величин, з якими нам доводиться мати справу”. Це питання в самій математиці може розглядатися самостійно. «Уявляється, однак, сумнівним, - указує Ф. Клейн, - чи можна такий поділ вважати за доцільне й з педагогічної точки зору».
Отже, позицію Ф. Клейна можна охарактеризувати в такий спосіб. По-перше, з його погляду, підхід до дробів як до пар цілих чисел хоча логічно й більше чистий, чим підхід з боку вимірювання, але й більш бідний, тому що не забезпечує застосування нових символів до вимірювання величин, «до зовнішнього світу». Саме цей недолік відсутній у шкільній традиції. По-друге, логічно чистий підхід не виводить людини за межі поняття про ціле число, не формує в неї належних наочних уявлень, що лежать в основі своєрідності дробів. Опора на вимірювання створює ці своєрідні уявлення, які досить істотні для практичної діяльності з величинами. По-третє, він захищає й підтримує педагогічну точку зору, відповідно до якої в основі переходу від цілих чисел до дробів повинне лежати нове уявлення учнів про вимірювані величини.
Досить оригінальну позицію в проблемі введення чисел у школі займав видатний французький математик А. Лебег. Він думав, що після натуральних чисел на основі виміру потрібно відразу переходити до походження й природи всієї області дійсних чисел (до нескінченних десяткових дробів), минаючи вивчення звичайних і навіть кінцевих десяткових дробів [9; 27].
Зміст цих поглядів А. Лебега були докладно проаналізовані

А.Н. Колмогоровим у передмові до книги «Про вимірювання величин», у якому він одночасно сформулював і ряд власних ідей про спосіб введення чисел у школі. На мій погляд, цей аналіз повчальний не тільки для викладачів математики й методистів, але й для психологів і дидактиків.

Тут важливий насамперед наступний висновок А. Н. Колмогорова: «Одне з основних завдань книги Лебега полягає в тому, щоб показати, що підхід до побудови раціональних і дійсних чисел з погляду вимірювання величин анітрошки не менш науковий, чим, наприклад, введення раціональних чисел у вигляді «пар». Для школи ж він має безсумнівні переваги. Першою перевагою є відповідність цього підходу історичному розвитку математики й наявному в учнів повсякденному досвіду. Другим же - та обставина, що він робить необхідним введення дійсних чисел» [9; 9].
А. Н. Колмогоров вважає, що А. Лебег правий постановці й принциповому рішенні цієї педагогічної задачі. Він також підтримує ідею А. Лебега про те, що для школи існує одна нероздільна задача - привести учнів до можливо більше ясного розуміння концепції дійсного числа. При її рішенні важливо зберегти єдність викладання математики на різних щаблях навчання. Для цього необхідно, щоб у початковій школі учні знайомилися з операцією вимірювання одержуючи з неї кінцеві десяткові дроби. На прикладі періодичних дробів, що виникають при діленні, можна закинути ідею про нескінченний дріб. У середній школі докладніше розбирається питання про точність вимірів, а потім через ряд етапів формулюється загальне поняття дійсного числа [9; 9-10; 14-15].
Таким чином, і для А. Лебега, і для А. Н. Колмогорова введення раціональних чисел на основі вимірювання величин не менш наукове ніж у вигляді «пар», крім того, воно відповідає історичному розвитку самої математики. Остання обставина особливо важливі. Справа в тому, що в математиці та й у її викладанні, часто трапляються випадки забуття реального походження понять, що веде до втрати їх первісного матеріального змісту. А. Лебег показав, як тісно ці поняття пов'язані з аналізом реальних процесів вимірювання. Протягом всієї книги він бореться за повернення математичним поняттям їхнього первісного змісту, за з'ясування їхнього реального походження, що .є умовою продуктивного вивчення математики. «У цій боротьбі, - пише А. Н. Колмогоров, - я й бачу основний інтерес книги Лебега» [9; 11].
Саме операція вимірювання надає раціональному й дійсному числу первісний матеріальний зміст, тому що ці числа є «знаряддям виміру величин» [10; 73]. На основі цієї операції в учнів можна сформувати правильне поняття про раціональні дроби, а потім підготувати ґрунт для переходу до ірраціональних чисел, тобто для роботи у всій області дійсних чисел. При цьому ті самі поняття спочатку повинні будуватися на наочній базі, потім формулюватися вже більш чітко й, нарешті, піддаватися тонкому логічному аналізу (останнє характерно для старших класів).
Як бачимо, загальна лінія, пов'язана із введенням дробів у школі, однакова у Ф. Клейна, А. Лебега й А. Н. Колмогорова. Відповідно до їхніх положень дроби по первісному походженню й матеріальному змісту мають тільки одне джерело вимірювання величин. У їхніх роботах взагалі немає мови про такі джерела, як ділення речей і чисел вимірювання величин й історично, і в сучасному викладанні є цілком повноцінною й перспективною основою введення дробових чисел.

РОЗДІЛ 2. МЕТОДИКА ВИВЧЕННЯ ДРОБІВ
2.1 Ознайомлення з частками
Ознайомити дітей з частками означає сформувати в них конкретні уявлення про частки, тобто навчити дітей утворювати частки практично. Наприклад, щоб дістати одну четверту частку круга, треба круг поділити на чотири рівні частини І взяти одну таку частину. Щоб дістати одну п'яту частку відрізка, треба поділити його на п'ять рівних частин і взяти одну таку частину.
Щоб сформувати правильні уявлення про частки, треба використати достатню кількість різних наочних посібників. Як показав досвід, найзручнішими посібниками є геометричні фігури, вирізані з паперу; можна використати рисунки фігур., виконані на папері або в діапозитивах (круги, прямокутники, трикутники, бруски, відрізки тощо). Дуже важливо, щоб посібники були не тільки в учителя, а й у кожного учня. Правильні уявлення про частки, а пізніше про дроби будуть сформовані тоді, коли учні своїми руками діставатимуть, наприклад, половину круга, квадрата тощо, чверть відрізка і т.д.
Покажемо, як можна ознайомити дітей з частками.
У кожного з учнів і в учителя є по кілька однакових кругів, прямокутників (квадратів).
Візьміть два однакові круги. Один з них поділіть на дві рівні частини (показує, як треба перегнути і як розрізати круг). Це один круг, а це - половина круга, інакше кажучи, одна друга частка круга. Скільки других часток у цілому крузі? (2.) Покажіть їх. Візьміть квадрат. Як дістати одну другу частку, чи половину квадрата? (Поділити його на дві рівні частини і взяти одну таку частину.) Виконуйте.
Учні можуть це зробити різними способами, наприклад: розрізати квадрат по діагоналі і дістати два рівні трикутники або розрізати квадрат по середині лінії, тоді утвориться два прямокутники. Деякі учні можуть запропонувати й інші способи поділу квадрата на дві рівні частини (Рис. 2).
Рис. 2
Як дістали одну другу частку круга? (Поділили круг на дві рівні частини і взяли одну таку частину.) Як дістали одну Другу частку квадрата? Як інакше називають одну другу частку круга, квадрата? (Половина круга, половина квадрата.) Скільки половин круга в цьому крузі? (2.)
Учні накладають половини круга на цілий круг.
Частки записують за допомогою двох чисел. Одну другу частку круга, квадрата позначають так: . Число 2 показує, що круг, квадрат або іншу фігуру (чи предмет) поділено на 2 рівні частини, а число 1 показує, що взяли одну таку частину.)
Учні записують на половинах круга « » і пояснюють, що показує в цьому записі кожне число.
Так само утворюють частки  та ін.
При цьому учні повинні усвідомити, що для того, щоб дістати, наприклад,  відрізка (прямокутника, паперової смужки тощо), треба цей відрізок (прямокутник, смужку) поділити на 5 рівних частин і взяти одну таку частину; що в цьому відрізку (прямокутнику, смужці) 5 п'ятих часток; що одну п'яту частку записують так: ; що в цьому записі число 5 означає, на скільки рівних частин поділили відрізок (прямокутник, смужку), а число 1 показує, що взято одну таку частку. Для закріплення цих знань і умінь учням пропонують різні вправи.
Це насамперед вправи на називання і записування часток (рис. 3). Назвіть і запишіть, яку частку квадрата (круга) відрізано (розмальовано, заштриховано).
Рис. 3
Можна пропонувати самим дітям зобразити яку-небудь частку відрізка (круга, квадрата і т.д.) і записати цю частку.
У кожному випадку треба записувати, скільки всього часток у цілому. Наприклад, скільки четвертих часток круга у цілому крузі? Скільки третіх часток відрізка в усьому відрізку? І т.д.
Ефективною вправою для формування уявлень про частки є практичне порівняння часток тієї самої величини за допомогою наочних посібників [1; 274].
Результати порівняння часток записуються за допомогою знаків “ < ” і “ > “. Наприклад,  > , що читається так: “Одна друга більше одної третьої”. Це можна записати і так:  <  і прочитати: “Одна третя менше одної другої”.
Ознайомити дітей із частками кожної і у такий спосіб. Учитель записує, хто бачив половину хліба (кавуна, яблука тощо), ставить завдання показати половину кружечка, розділити навпіл смужку паперу. Перегинаючи круг, смужку паперу навпіл, діти роблять висновок, що половини одного і того самого круга чи тієї самої смужки паперу рівні між собою. На цьому самому уроці вони розглядають малюнок.
Перша смужка поділена на 3 рівні частини, а друга - на 4. Знайдіть, чому дорівнює третя і четверта частини смужки. Третя частина ще називається третина, а четверта - чверть. Покажіть на малюнках третю і четверту частини круга.
 

третя частина

четверта частина

Учні знаходять половину числа 12, третину числа 15, чверть числа 8 та ін.
Діти повинні усвідомити, що для знаходження половини числа його треба поділити на 2, для знаходження третини - поділити на 3, для знаходження чверті - поділити на 4.
Наприкінці навчання у 2 класі і впродовж 3 класу учні знаходять довжини вказаних частин смужки, частини чисел (без позначення частин числа цифрами). Приклади:
1. Знайдіть половину, третину і чверть числа 12.
2. Виміряйте довжину кожної смужки, а потім знайдіть довжину четвертої частини першої смужки і шостої частини другої. Результати обчислення перевірте вимірюваннями (рис. 4).

четверта частина
шоста частина
Рис. 4
3. Знайдіть п'яту частину 1дм, четверту частину 2дм, половину 1м.
4. Скільки хвилин становить одна шоста години? Одна четверта? Одна третя? Половина години?
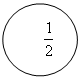
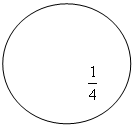
У 3 класі дітей вчать позначати частини цифрами, їм потрібно спочатку показати поділ першого круга на дві рівні частини, другого - на чотири рівні частини. Тоді необхідно з'ясувати з ними, на скільки рівних частин поділені дані круги. Після цього слід розглянути малюнки в підручнику
Рис. 5
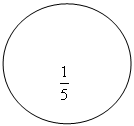Учитель пояснює, що частини записують за допомогою двох цифр. Наприклад, третю частину круга, смужки позначають так: 1/3. Число 3 показує, що круг, смужку або іншу фігуру поділили на три рівні частини, а число 1 показує, що взяли одну таку частину. Терміни «чисельник», «знаменник» не вводять. Просто кажуть, що число під рискою показує, на скільки рівних частин поділили круг (смужку), а число над рискою показує, що взяли одну таку частину.
Під час виконання вправ на знаходження частини смужки (круга, квадрата тощо) доцільно звертати увагу учнів, що в цілій смужці (крузі, квадраті) є дві половини, три третіх частини, чотири четвертих частини і т. ін.
В результаті ознайомлення з частками і їх отриманням діти повинні навчитися з опорою на малюнок порівнювати частки і знати, наприклад, що в цілому відрізку дві половинки, три третіх частки, чотири четвертих частки і т.д.
Тільки після того, як вчитель переконається в тому, що кожен з учнів це уявляє, можна переходити до розв‘язування простих задач, де потрібно знайти частку числа [3; 270].
Розв‘язування задач на знаходження частки числа і числа за його часткою також сприяє формуванню уявлень про частки величини. У цьому їх основне призначення. Тому задачі на знаходження частки числа і числа за його часткою розв‘язують на наочній основі.
Розглянемо, як можна ознайомити учнів з розв‘язуванням задач кожного виду.
Спочатку вводять задачі на знаходження частки числа. Для ознайомлення з розв‘язуванням задач краще пропонувати задачі, які легко ілюструвати. Наприклад, пропонують задачу: «Від смужки довжиною 15см відрізали  її. Чому дорівнює довжина відрізаної смужки?» Учні відрізують смужку довжиною 15см. Потім з‘ясовують, як знайти одну третю частину смужки (поділити її на 3 рівні частини і взяти одну таку частину). Учні практично ділять смужку (перегинають її), а потім відрізують одну третю частину. Розв‘язання записують так:
15 : 3 = 5(см). Відповідь: 5см.
Під час розв‘язування інших задач досить скористатись кресленням: число зобразити відрізком, який учні ділять на задане число рівних частин, позначають частку, після чого розв‘язують усно або письмово.
Потім дають задачі на знаходження частки числа для усної та письмової роботи. Треба більше давати завдань виду: скільки сантиметрів у м., в м., в м.? Скільки хвилин в  години; в  години; в  години і т.д.?
Вивчаючи тему «Час», треба пояснити дітям, чому кажуть: «половина на другу», «без чверті десята» тощо.
Задачі на знаходження числа за його часткою спочатку треба брати такі, щоб їх можна було безпосередньо ілюструвати, наприклад: «Сергійко відрізав від дротини 4см. Це  всієї дротини. Яка довжина дротини?»
Зобразимо кусок дротини, який відрізав Сергійко (креслять відрізок довжиною 4см.). Яку частину всієї дротини становить відрізаний кусок? ( ). Як зобразити всю дротину? (Взяти 3 рази по 4см.). Чому? (4см. – це  дротини, а в усій дротині буде три треті). Накресліть. (Виконують). Якої довжини була дротина? (12см.). Як дізнатися? (4,3).
Запис розв‘язання: 4 ∙ 3 = 12. Відповідь: 12см.
Для задачі на знаходження числа за його часткою і задачі на знаходження частки числа вводять по черзі і пропонують як для усного, так і для письмового розв‘язування. Краще розв‘язувати задачі з конкретним змістом, а не з абстрактними числами (щоб учні конкретно уявляли частку величини (одну третину відра води, чверть кошика яблук, одну п‘яту частину сувою тканини, одну соту частину метра тощо) [1; 275-276].
Не варто формулювати спеціальні правила для розв‘язування задач, пов‘язаних зі знаходженням частки числа чи числа за його відомою часткою. Формальний підхід, як це показує практика, може привести до того, що діти починають плутати ці два різновиди задач, допускають помилку при виборі дії.
Добре засвоєння того, що дві половини, чи три третіх, чи чотири четвертих частки утворює ціле, весь предмет, лежить в основі розв‘язування задач на знаходження числа за його відомою часткою. Перші задачі такого типу розв‘язуються з опорою на реальні речі [10; 251].
2.2 Ознайомлення з дробами
Ознайомлення учнів з дробовими числами у формі звичайних дробів проводиться у зв‘язку з вивченням множення і ділення багатоцифрових чисел і ґрунтується на уявленнях, знаннях, вміннях і навичках, вироблених учнями при ознайомленні з частками величин (числа). Методика ознайомлення з простими дробами ґрунтується в основному на конкретних образах часток величини, на практичному отриманні тої чи іншої частки, а потім і дробу, шляхом ділення предметів, геометричних фігур на потрібне число рівних частин тощо. Тут не допускається спроба формально дати визначення цих понять.
В залежності від підготовки класу до вивчення теми «Дроби» може бути відведено 7-8 уроків. Причому до уроків, на яких діти знайомляться з новим для них матеріалом – дробами, включається (50%) матеріал, пов‘язаний з оволодінням техніки обчислень, розв‘язуванням задач.
В результаті вивчення цієї теми учні повинні:
1) вміти називати і показувати частки з знаменниками, які не перебільшують числа 10, знати назви таких часток, як  (половини, третини, чверті);
2) вміти читати і записувати звичайні дроби із знаменниками, які не перевищують числа 10, вміти називати знаменник і чисельник дробу і показувати відповідний дріб відрізка (круга, прямокутника);
3) вміти порівняти (з опорою на малюнок) вказані вище дроби. Без опори на малюнок вміти порівняти дроби, у яких чисельник дорівнює 1 (  і т.д.);
4) вміти розв‘язувати задачі на знаходження частки числа і числа за його часткою, а також на знаходження дробу числа.
Формування названих знань, умінь і навичок досягається в процесі практичної діяльності учнів при розв‘язуванні системи спеціально підібраних задач і з застосуванням необхідного мінімуму навчального обладнання серед них:
1) набір (демонстраційний) кругів і прямокутників (паперових чи картонних), розділених на різне число часток;
2) таблиці;
3) набір паперових прямокутників (смужок) довжиною 10см чи 12см (на кожного учня по 8-10 смужок) для проведення практичних робіт;
4) карточки-завдання з математики, навчальні діафільми.
Перший з уроків, присвячених ознайомленню учнів із звичайними дробами, починається короткою бесідою, в процесі якої (із застосуванням таблиць і набору паперових фігур) активізуються уявлення учнів про частки величини – одну із рівних частин, на які поділений відрізок.
На наступному уроці відведеного для подальшого ознайомлення учнів з дробами, опираючись вже на знання учнів, розглядають важливий факт, від усвідомлення якого у подальшому залежить розуміння основної властивості дробу, розуміння способу отримання дробів з іншими знаменниками, порівняння дробів з однаковими чисельниками тощо [10; 327-328].
Як наочні посібники для ознайомлення з дробами можна використати такі.
Поділіть круг на чотири рівні частини. Як назвати кожну таку частину? Запишіть. Покажіть три чверті частки. Ви дістали дріб – три чверті. Хто може записати цей дріб? Що показує число 4? (На скільки рівних частин поділили круг). Що показує число 3? (Скільки таких частин узяли). Аналогічно учні дістають і записують інші дроби, пояснюючи, що показує кожне число.
Для закріплення здобутих знань розв‘язують такі самі вправи, які і під час знайомлення з частками за даними ілюстраціями називають і записують, які дроби зображені, або зображують дріб за допомогою креслення, рисунка. Засвоєнню конкретного змісту дробу допомагають вправи на порівняння дробів, а також розв‘язування задач на знаходження дробу числа.
Для порівняння дробів звичайно використовують ілюстрації з однаковими прямокутниками.

			1

Учням пропонують накреслити в зошиті прямокутник, довжина якого 16см., а ширина 1см. Це один прямокутник. Запишемо (у першому прямокутнику записують число 1). Накресліть під першим прямокутником такий самий другий і поділіть його на дві рівні частини. (Виконують). Які частки дістали? (Другі, половини). Скільки других часток у цілому прямокутнику?
Підпишіть. Нижче накресліть такий самий прямокутник і поділіть його на 4 рівні частини. Як називається кожна частина? Скільки четвертих часток у цілому прямокутнику? Скільки четвертих часток у .половині? Що більше: одна друга чи одна четверта; одна друга чи дві четверті; одна четверта чи три четверті; дві другі чи чотири четверті? Накресліть четвертий такий самий, прямокутник і поділіть його на 8 рівних частин. Як називаються утворені частки? Скільки восьмих часток у цілому? Скільки восьмих часток в одній чверті; у половині прямокутника? Що більше: три восьмих чи одна четверта? Якому дробу дорівнює одна друга? .......
Відповіді на всі такі запитання діти дають, користуючись рисунком: порівнюючи, наприклад,  і , вони з рисунка бачать, що  більше, ніж  того самого прямокутника. Таким самим способом порівнюють і інші дроби, але для порівняння їх використовують інші ілюстрації: наприклад, для порівняння дробів із знаменниками 3, 6 і 9 однакові прямокутники ділять відповідно на З, 6 і 9 рівних частин, а для порівняння дробів із знаменниками 2, 5 і 10 однакові прямокутники ділять відповідно на 2, 5 і 10 рівних частин. Пропонують спеціальні вправи на порівняння дробів:
1) Вставте пропущений знак «>», «<» або « = »:
;                   1;                   .
2) Підберіть таке число, щоб рівність (нерівність) була правильна:

5	=		;	3	>		;	1	<	
10		2		8		4		2		4

Виконуючи такі вправи, учні використовують відповідні ілюстрації з прямокутниками або заново зображують дроби за допомогою, наприклад, відрізків. Так, порівн.юючи дроби  і , учень виконує рисунок (Рис. 6) і міркує так: «Зображу на відрізку дріб ; для цього відрізок поділю на 8 рівних частин і візьму 3 таких частини; зображу на такому самому відрізку дріб ; поділю відрізок на 4 рівні частини і візьму 3 таких частини; відразу видно, що  відрізка більше, ніж  його. Запишу: > ».

Конкретний зміст дробу дуже яскраво розкривається під час розв'язування задач на знаходження дробу числа. Ці задачі, як і задачі на знаходження частки числа, розв'язують за допомогою відповідних наочних посібників.
Наприклад, пропонують задачу. «У монтера було 12м проводу. - всього проводу він витратив. Скільки метрів проводу витратив монтер?»
Учні під керівництвом учителя виконують рисунок (рис. 7). Зобразимо відрізком кусок проводу, взявши 1см за 1м. Якої довжини відрізок треба накреслити? (12см.) Що сказано про витрачений провід? (Витрачено  всього проводу). Як зобразити витрачений кусок проводу? (Відрізок поділити на 3 рівні частини і взяти 2 такі частини.) Отже, спочатку ми 12 поділимо на 3. Про що дізнаємось? (Чому дорівнює  проводу.) Чому ж вона дорівнює? (4м.) Потім результат помножимо на 2. Про що дізнаємося? (Чому 2 дорівнює  проводу.) Скільки ж метрів проводу витратив монтер? (8м.)
Запис: 12:3-2=8 м. Відповідь: 8м.
Пізніше, розв'язуючи такі задачі, учні повинні самостійно міркувати. Наприклад: треба визначити, скільки хвилин у  год. Учень міркує: «Знайду, скільки хвилин становить  год, для цього 60 поділю на 4, буде 15; тепер знайду, скільки хвилин у  год, для цього 15 помножу на 3, буде 45; отже, год - це
45 хв».
Задачі на знаходження дробу числа треба пропонувати як для усного, так і для письмового розв'язування.
Трохи пізніше задачі на знаходження дробу числа треба включити до складених задач, наприклад: «Мотоцикліст проїхав за 3 дні 1250км. За перший день він проїхав  всього шляху, а за другий -  усього шляху. Яку відстань проїхав мотоцикліст за третій день?».

Рис.7
Записувати розв‘язування таких задач краще у вигляді окремих дій:
1) 1250 : 5 ∙ 2 = 500(км.) – проїхав мотоцикліст першого дня;
2) 1250 : 10 ∙ 3 = 375(км.) – проїхав мотоцикліст другого дня;
3) 500 + 375 = 875(км.) – проїхав мотоцикліст за 2 дні;
4) 1250 – 875 = 375(км.) – проїхав мотоцикліст третього дня.
Відповідь: 375км. [1; 278].
Різні вправи з дробами слід частіше включати для усних і письмових робіт протягом усього навчального року. Це можуть бути такі вправи:
1. На скільки рівних частин поділено кожний квадрат?
Як називається не заштрихована частина у квадраті? Скільки таких частин у квадраті заштриховано?
2. Полічіть, на скільки рівних частин поділено кожний круг?

Скільки таких частин заштриховано?
Ми вже вміємо позначати цифрами одну частину числа. Яка частина першого круга заштрихована? (1/6). (Учитель записує це число на дошці). Скільки таких шостих частин заштриховано у другому крузі? (2). Тобто заштриховано 2/6 частини. (Вчитель записує на дошці). Скільки таких шостих частин заштриховано у третьому крузі? І т. д.
Числа виду 1/2, 2/3, 3/4, 1/6, 2/3, 5/6 називаються дробовими числами, Число 5/6 - дріб, 5 - чисельник дробу, а 6 - знаменник дробу. Число під рискою дробу - знаменник дробу - показує, на скільки рівних частин поділено ціле. Число над рискою дробу - чисельник дробу - показує, скільки взято рівних частин цілого.
Для закріплення матеріалу учні виконують такі вправи:
а) запишіть у вигляді дробу, яку частину прямокутника заштриховано
б) прочитайте дроби і поясніть, як їх утворено.

Здобуті знання про дроби та їх зображення використовують під час розв'язування задач на знаходження дробу від числа. Пояснення знаходження дробу від числа подають на основі готового розв'язання.
Задача. Довжина відрізка А В дорівнює 10см. Чому дорівнює 3/5 цього відрізка ?
10см.

Розв'язання
1) Скільки сантиметрів в 1/5 відрізка АВ?
10 : 5 = 2(см).
2) Чому дорівнює 3/5 відрізка АВ?
2 ∙ 3 = 6 (см).
Відповідь. Довжина 3/5 відрізка АВ дорівнює 6см.
Пропонують учням і абстрактні задачі на знаходження дробу від числа. Задача. Знайдіть 5/9 від 64 260.
64 260 : 9 ∙ 5 = 35 700.
У 4 класі діти розв'язують складені задачі, що передбачають знаходження дробу, а саме:
1. Задачі, в яких треба знайти кілька частин від даного числа (знайти дріб від числа).
Задача. Маса гарбуза дорівнює 14кг. Від гарбуза відрізали 2/7 його маси і зварили кашу. Скільки кілограмів гарбуза було витрачено на кашу?
2. Задачі, в яких треба знайти кілька частин від решти.
Задача. Площа дослідного поля становить 86 000м². Частину цього поля у вигляді прямокутної ділянки зі сторонами 320м і 100м засіяно гречкою, 3/4решти поля засіяно просом. Скільки квадратних метрів становить площа поля, засіяна просом?
3. Задачі, в яких треба знайти кілька частин від того числа, яке знайшли. Задача. Туристу треба було пройти 180км. За перший день він пройшов
1/6 всього шляху, а за другий- 4/5 того шляху, який пройшов за перший день. Скільки кілометрів пройшов турист за два дні?
Завдання на знаходження дробу від числа часто пропонують для усних обчислень. Вони корисні для закріплення учнями знань про співвідношення між мірами величин. Наприклад:
1. Скільки метрів у 3/4 км? У 2/5 км? У 3/10 км?
2. Скільки кілограмів у 3/4 ц? У 3/4 т? У 3/5 ц? ,
3. Знайдіть: 2/7 від 35; 3/4 від 40; 2/5 від 200. [3; 273-274].

ВИСНОВКИ
Дроби мають широке застосування в повсякденному житті. Це зумовлює потребу у формуванні уявлень про дроби уже в початковій школі. Проте, разом з тим, викладання дробів у молодших класах пов‘язане з певними труднощами, які з однієї сторони змушують різко обмежити об‘єм знань про дроби, з якими ознайомлюють молодших школярів, а з іншої сторони, викликає тенденцію до такого способу введення дробів, який не відповідає поняттю про них.
У молодших школярів необхідно створити конкретні уявлення про процес утворення частин від цілого предмета чи сукупності предметів. З цією метою вже в 3 класі дітей ознайомлюють з частинами, їх записом, вчать знаходити частину числа та число за відомою його частиною. У класі продовжують працювати над засвоєнням частини числа, учнів ознайомлюють з дробами та їх записом, вчать порівнювати частини, знаходити кілька частин від числа, дробів від числа, розв‘язувати складені задачі, що передбачають знаходження дробу від числа.
Розглядають ці питання з допомогою наочності, виконуючи практичні вправи, пов‘язані з кресленням, вимірюванням, перегинанням, практичним поділом круга, прямокутника, смужки на рівні частини.
Формування поняття про дроби рекомендується проводити по трьох основних етапах:
1) спочатку діти засвоюють фактичне роздроблення (ділення) різноманітних конкретних предметів на рівні частини; утворюють із частин дроби;
2) потім цю ж роботу діти проробляють уже на кресленнях (малюнки кругів, відрізків);
3) діти оперують дробами по уявленню.
Ознайомити дітей з частками означає сформувати в них конкретні уявлення про частки, тобто навчити дітей утворювати частки практично. Щоб сформувати правильні уявлення про частки, треба використати достатню кількість різних наочних посібників. Як показав досвід, найзручнішими посібниками є геометричні фігури, вирізані з паперу; можна використати рисунки фігур, виконані на папері. Дуже важливо, щоб посібники були не тільки в учителя, а й у кожного учня. Правильні уявлення про частки, а пізніше про дроби будуть сформовані тоді, коли учні своїми руками діставатимуть, наприклад, половину круга, квадрата, чверть відрізка тощо.
Формування уявлень про частку величини також сприяє розв‘язування задач на знаходження частки числа і числа за його часткою. Ці задачі розв‘язують на наочній основі. Не слід формулювати спеціальних правил для розв‘язування цих задач. Формальний підхід, як це показує практика, може привести до того, що діти починають плутати ці дві задачі, допускають помилку при виборі дій.
Утворення дробів, як і утворення часток, розглядають за допомогою наочних посібників.
Для закріплення здобутих знань розв‘язують такі самі вправи, як і під час знайомлення з частками: за даними ілюстраціями називають і записують, які дроби зображені, або зображують дріб за допомогою креслення, рисунка. Засвоєнню конкретного змісту дробу допомагають вправи на порівняння дробів, а також розв‘язування задач на знаходження дробу числа.
Ознайомлюючи учнів із дробами слід опиратися на досвід учнів, знання, поновити їх і систематизувати.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1) Бантова М.А., Бельтюкова Г.В., Полевщикова О.В. Методика викладання математики в початкових класах. – К.: Вища школа, 1977. – С. 273-279.
2) Богданович М.А., Будна Н.О., Лисенко Г.П. Урок математики в початковій школі: Навчальний посібник. – Тернопіль: Богдан, 2004. – 280с.
3) Богданович М.В., Козак М.В., Король Я.А. Методика викладання математики в початкових класах: Навчальний посібник. – Тернопіль: Богдан, 2006. – С. 269-274.
4) Андронов И.К. Арифметика дробных чисел и основных величин. – М.: Учпедгиз, 1955. – С. 7-12.
5) Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах. – М.: Просвещение, 1985. – С. 302-309.
6) Блонский П.П. Избранные психологические произведения. – М.: Просвещение, 1964. – С. 162-163.
7) Давыдов В.В., Психологические возможности младших школьников в усвоении математики. – М.: Просвещение, 1969. – С. 76-130.
8) Депман И.Я. История арифметики. – М.: Учпедгиз, 1959. – С. 239-264.
9) Лебег А. Об измерении величин. – М.: Учпедгиз, 1960. – С. 8-27.
10) Моро М.И., Пынькало А.М. Методика обучения математике в І-ІІІ классах: Пособие для учителя. – М.: Просвещение, 1978. – С. 250-331.
11) Пчелко А.С. Основы методики начального обучения. – М.: Просвещение, 1965. – С. 325-331.
12) Шевченко И.Н. Методика преподавания арифметики в V-VI классах. – М.: АПН РСФСР, 1961. – С. 80-95.