Курсовая на тему Использование метода ветвей и границ при адаптации рабочей нагрузки к параметрам вычислительного
Работа добавлена на сайт bukvasha.net: 2014-12-08Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
«Гомельский государственный университет имени Франциска Скорины»
Математический факультет
Кафедра МПУ
Курсовая работа
"Использование метода ветвей и границ при адаптации рабочей нагрузки к параметрам вычислительного процесса"
Гомель 2002
Реферат
Курсовая работа 25 страниц, 10 источников, 5 рисунков, 1 таблица
Ключевые слова: ИМИТАЦИОННАЯ МОДЕЛЬ, МЕТОД ВЕТВЕЙ И ГРАНИЦ, ПОЛУМАРКОВСКИЕ ПРОЦЕССЫ, ВЫЧИСЛИТЕЛЬНАЯ СИСТЕМА, ВЫЧИСЛИТЕЛЬНЫЙ ПРОЦЕСС, ПРОГРАММНЫЙ МОДУЛЬ, ГРАФ, МАТРИЦА ВЕРОЯТНОСТЕЙ, МЕТОД МОНТЕ-КАРЛО
Объект исследования: имитационная модель процесса обработки данных.
Предмет исследования: применение метода ветвей и границ в процессе обработки данных.
Цель курсовой работы: найти рациональный порядок следования запросов, который обеспечит максимальный критерий эффективности использования компонентов вычислительного процесса в вычислительной системе.
Задачами курсовой работы являются: изучить метод ветвей и границ и применить его к модели машинного моделирования, позволяющей найти такой порядок следования запросов, который обеспечит максимально быстрое выполнение вычислительного процесса.
Выводы: с помощью метода ветвей и границ удаётся построить такой порядок выполнения запросов, при котором время их обслуживания будет минимальным.
Содержание
Введение
1. Марковские процессы
2. Метод Монте-Карло
2.1 Общая характеристика метода Монте-Карло
2.2 Точность метода
3. Метод ветвей и границ
4. Построение оптимальной последовательности заданий на обработку в узле вычислительной системы
4.1 Формализация вычислительного процесса и рабочей нагрузки
4.2 Особенности организации имитационного эксперимента
4.3 Модификация последовательности решения задач в пакете по методу ветвей и границ
Заключение
Список источников
Введение
Выбором рабочей нагрузки под вычислительный процесс в вычислительных системах занимались многие исследователи. Однако все они оперировали интегральными характеристиками решения задач, не рассматривая при этом динамику использования ресурсов вычислительных систем во времени выполнения задач и пространстве параметров. Такой подход иногда приводил к существенной ошибке в оценке производительности системы в условиях, когда задания сильно конкурируют за ресурсы вычислительной системы. Это обстоятельство определило актуальность задачи адаптации рабочей нагрузки под возможности вычислительных систем в условиях, когда технология их обработки рассматривается на высоком уровне детализации. В данной работе будем исходить из следующих допущений:
1. Каждое задание вероятностным образом использует различные ресурсы вычислительного процесса, а сам вероятностный процесс является полумарковским.
2. Исследователю известны заранее характеристики полумарковского процесса, реализуемого каждым из заданий, или же имеются инструментальные средства для измерения этих характеристик.
3. Поток заданий постоянно используется на данной вычислительной системе и имеет практически неизменную структуру запросов ресурсов вычислительной системы, что позволяет говорить о принципиальной возможности нахождения такого порядка заданий, который является оптимальным при заданном составе ресурсов вычислительной системы.
1. Марковские процессы
Пусть имеется система, которая в произвольный момент времени tk может находиться в одном из состояний si, 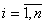
, с вероятностью 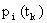
. Через некоторые промежутки времени система переходит из одного состояния в другое. Каждый такой переход называется шагом процесса. Случайный процесс, протекающий в системе S, называется марковским, если для произвольного момента времени 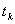
вероятность любого состояния системы в будущем (при 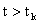
) зависит только от её состояния в настоящем (при 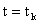
) и не зависит от того, когда и каким образом система пришла в это состояние. Различают марковские процессы с дискретными состояниями и дискретным временем (стохастическая последовательность, или дискретная цепь Маркова) и марковские процессы с дискретным состоянием и непрерывным временем (непрерывная цепь Маркова). Оба типа цепей могут быть однородными и неоднородными.
Для дискретной цепи Маркова смены состояний процесса происходят в дискретные моменты времени ti с шагом 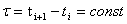
. Состояние системы si в момент tk необходимо характеризовать условными вероятностями 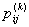
(1) того, что система за один шаг перейдёт в какое-либо состояние sj при условии, что в момент tk-1 она находилась в состоянии si. Вероятности 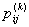
(1) = 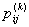
являются основными характеристиками марковской цепи. Они называются вероятностями перехода или переходными вероятностями. Поскольку система может находиться в одном из состояний, то для каждого момента времени tr необходимо задать n2 вероятностей перехода 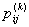
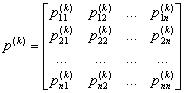
.
Эта матрица называется матрицей переходных вероятностей или матрицей переходов. Для неё справедливо выражение 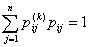
, 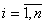
. Матрица переходных вероятностей обязательно является квадратной матрицей с неотрицательными элементами, образующими по строкам единичную сумму; матрица такого рода называется стохастической. В случае, когда вероятности перехода не зависят от времени, а зависят только от величины τ и не изменяются при сдвиге вдоль временной оси, цепь Маркова называется однородной. Для такой цепи задаётся матрица
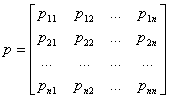
.
Вероятности перехода представляют собой важнейшие характеристики любой марковской цепи. Однако они по определению являются условными, и поэтому знание матрицы переходных вероятностей не полностью определяет цепь Маркова. Если отнести матрицу переходов к первому шагу, определяющему начало работы системы, то для исключения условностей необходимо задать ещё вероятности начальных состояний.
Вероятности начальных состояний 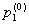
, 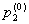
,…, 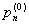
являются безусловными вероятностями и образуют матрицу-строку 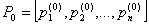
, сумма элементов которой по условию нормировки должна быть равна 1.
Матрица переходов даёт исчерпывающее представление о вероятностях возможных переходов за один шаг. Естественно возникает вопрос: как рассчитать вероятности того, что система, находящаяся в данный момент в состоянии si, переходит в состояние sj за r шагов. Матрица переходов за r шагов P(r) вычисляется как r-я степень матрицы перехода за один шаг P(r)=pr. Безусловные вероятности системы на r-м шаге определяются из выражений: 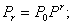
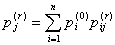
.
Различают цепи эргодические и поглощающие. Это различие основано на классификации состояний. Состояние si называется невозвратным, если существуют такие состояния sj ( 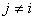
) и число шагов r, что pij(r)>0, но pij(q)=0 для всех q. Все остальные состояния называются возвратными. Таким образом, из невозвратного состояния всегда можно с положительной вероятностью и за какое-либо число шагов перейти в некоторое другое состояние. В то же время вернуться из этого состояния в первоначальное невозможно.
Если выбрать такие состояния si и sj, что для них при некоторых r и q выполняется неравенство pij(r)>0, pji(r)>0, то они называются сообщающимися. Если sj сообщается с si, а si с sk, то sj сообщается с sk. Это обстоятельство позволяет разделить множество возвратных состояний на классы (подмножества) сообщающихся состояний. Состояния, принадлежащие к различным классам, не сообщаются между собой. Если множество возвратных состояний состоит из одного класса, то оно называется эргодическим. Существуют так называемые поглощающие состояния, например если si – поглощающее состояние, то pii=1, pij=0. Цепи Маркова, не содержащие возвратные множества и образующие эргодическое множество, называются эргодическими. Свойства и методы расчетов параметров поглощающих и эргодических цепей различны.
Для непрерывной цепи Маркова вводится понятие плотности вероятности перехода (интенсивность потока событий) как предела отношения вероятности перехода системы за время Δt из состояния i в состояние j к длине промежутка:
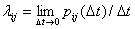
( 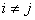
).
Если λij не зависит от t, то есть от того, в какой момент начинается Δt, то непрерывная цепь Маркова называется однородной, в противном случае она называется неоднородной.
Однородная цепь Маркова характеризуется тем, что все потоки, переводящие систему из одного состояния в другое, являются простейшими, то есть стационарными пуассоновскими потоками. При этом время непрерывного пребывания цепи в каждом состоянии распределено по экспоненциальному закону.
Для неоднородной цепи промежутки времени между соседними событиями распределены не по показательному закону.
Если непрерывная цепь Маркова является однородной и между любыми её двумя состояниями существует маршрут, то она эргодичная. Кроме того, если вероятности состояний системы pj не зависят от времени наблюдения системы и совпадают с её начальными вероятностями состояний 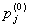
и стационарными вероятностями, т.е. 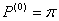
, то режим цепи является стационарным.
Отметим, что понятия «стационарность управляющих потоков» и «стационарный режим» совершенно разные и из первого не следует второе. Таким образом, однородная непрерывная цепь Маркова определяется начальным распределением вероятностей 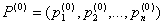
, матрицей интенсивностей [λij] простейших потоков, где λij=pijλi, вектором экспоненциально распределённых времён пребывания в состояниях с параметрами {1/μ1, 1/μ2, …, 1/μn}.
Главное отличие полумарковского процесса от цепи Маркова состоит в отказе от требования, чтобы распределения времени пребывания в каждом состоянии подчинялись показательному закону. Обычно полумарковский процесс задаётся начальным распределением вероятностей 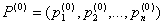
, матрицей переходных вероятностей [pij] и совокупностью произвольных функций распределения времени пребывания в состояниях 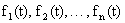
.
В моменты переходов из одного состояния в другое полумарковский процесс обладает марковским свойством. Если рассматривать полумарковский процесс только в моменты переходов, то получающаяся при этом марковская цепь с дискретным временем называется вложенной марковской цепью (так как она содержится в полумарковском процессе). Вложенная цепь имеет то же пространство состояний S и тот же вектор P(0) начального распределения вероятностей состояний, что и полумарковский процесс, а матрицей переходов вложенной цепи является матрица P=[pij] полумарковского процесса.
Для эргодических полумарковских процессов, как и для эргодических марковских цепей, характерно наличие стационарного режима.
2. Метод Монте-Карло
Различные методы и приборы для определения параметров и характеристик случайных процессов можно объединить в две группы. Первую группу составляют приборы для определения корреляционных функций (корреляторы), спектральных плотностей (спектрометры), математических ожиданий, дисперсий, законов распределения и прочих случайных процессов и величин.
Все приборы первой группы можно разделить на две подгруппы. Одни определяют характеристики записанных случайных сигналов за достаточно большое время, намного превышающее время реализации самого случайного процесса. Другие (они в последнее время вызывают наибольший интерес) позволяют получать характеристики случайного процесса оперативно, в такт с поступлением информации при натурных испытаниях новых систем управления, так как, пользуясь их показаниями, можно непосредственно изменять процесс управления и в ходе эксперимента наблюдать за результатами этих изменений.
Вторая группа содержит методы и приборы, предназначенные для исследования случайных процессов и главным образом систем управления, в которых присутствуют случайные сигналы, на универсальных цифровых и аналоговых вычислительных машинах. Иногда для таких исследований приходится создавать специализированные вычислительные машины цифрового, аналогового или чаще всего аналого-цифрового (гибридного) типа, так как существующие типовые машины не приспособлены для решения некоторых задач.
Широко применяется на практике метод Монте-Карло (метод статических испытаний). Его основная идея чрезвычайно проста и заключается по существу в математическом моделировании на вычислительной машине тех случайных процессов и преобразований с ними, которые имеют место в реальной системе управления. Этот метод в основном реализуется на цифровых и, реже, на аналоговых вычислительных машинах.
Можно утверждать, что метод Монте-Карло остаётся чистым методом моделирования случайных процессов, чистым математическим экспериментом, в известном смысле лишённым ограничений, свойственным другим методам. Рассмотрим данный метод применительно к решению различных задач управления.
2.1 Общая характеристика метода Монте-Карло
Как уже указывалось, идея метода Монте-Карло (или метода статистического моделирования) очень проста и заключается в том, что в вычислительной машине создаётся процесс преобразования цифровых данных, аналогичный реальному процессу. Вероятностные характеристики обоих процессов (реального и смоделированного) совпадают с какой-то точностью.
Допустим, необходимо вычислить математическое ожидание случайной величины X, подчиняющейся некоторому закону распределения F(x). Для этого в машине реализуют датчик случайных чисел, имеющий данное распределение F(x), и по формуле, которую легко запрограммировать, определяют оценку математического ожидания:
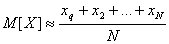
.
Каждое значение случайной величины xi представляется в машине двоичным числом, которое поступает с выхода датчика случайных чисел на сумматор. Для статистического моделирования рассматриваемой задачи требуется N-кратное повторение решения.
Рассмотрим ещё один пример. Производится десять независимых выстрелов по мишени. Вероятность попадания при одном выстреле задана и равна p. Требуется определить вероятность того, что число попаданий будет чётным, т.е. 0, 2, 4, 6, 8, 10. Вероятность того, что число попаданий будет 2k, равна:
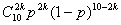
,
откуда искомая вероятность
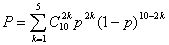
(1)
Если эта формула известна, то можно осуществить физический эксперимент, произведя несколько партий выстрелов (по десять в каждой) по реальной мишени. Но проще выполнить математический эксперимент на вычислительной машине следующим образом. Датчик случайных чисел выдаст в цифровом виде значение случайной величины ξ, подчиняющейся равномерному закону распределения в интервале [0,1]. Вероятность неравенства ξ<p равна p, т.е.
P {ξ<p}=p.
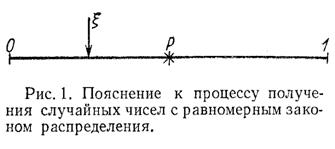
Для пояснения целесообразно обратиться к рис. 1, на котором весь набор случайных чисел представляется в виде точек отрезка [0,1]. Вероятность попадания случайной величины ξ, имеющей равномерное распределение в интервале [0,1], в интервал [0, p] (где 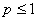
) равна длине этого отрезка, т.е. p. Поэтому на каждом такте моделирования полученное число ξ сравнивают с заданной вероятностью p. Если ξ<p, то регистрируется попадание в мишень, в противном случае – промах. Далее проводят серию из десяти тактов и подсчитывают чётное или нечётное число попаданий. При большом числе серий (100–1000) получается вероятность, близкая к той, которая определяется по формуле (1).
Различают две области применения метода Монте-Карло. Во-первых, для исследования на вычислительных машинах таких случайных явлений и процессов, как прохождение элементарных ядерных частиц (нейтронов, протонов и пр.) через вещество, системы массового обслуживания (телефонная сеть, система парикмахерских, система ПВО и пр.), надёжность сложных систем, в которых выход из строя элементов и устранения неисправностей являются случайными процессами, статистическое распознавание образов. Это – применение статистического моделирования к изучению так называемых вероятностных систем управления.
Этот метод широко применяется и для исследования дискретных систем управления, когда используются кибернетические модели в виде вероятностного графа (например, сетевое планирование с β-распределением времени выполнением работ) или вероятностного автомата.
Если динамика системы управления описывается дифференциальными или разностными уравнениями (случай детерминированных систем управления) и на систему, например угловую следящую систему радиолокационной станции воздействуют случайные сигналы, то статическое моделирование также позволяет получить необходимые точностные характеристики. В данном случае с успехом применяются как аналоговые, так и цифровые вычислительные машины. Однако, учитывая более широкое применение при статистическом моделировании цифровых машин, рассмотрим в данном разделе вопросы, связанные только с этим типом машин.
Вторая область применения метода Монте-Карло охватывает чисто детерминированные, закономерные задачи, например нахождение значений определённых одномерных и многомерных интегралов. Особенно проявляется преимущество этого метода по сравнению с другими численными методами в случае кратных интегралов. «Гомельский государственный университет имени Франциска Скорины»
Математический факультет
Кафедра МПУ
Курсовая работа
"Использование метода ветвей и границ при адаптации рабочей нагрузки к параметрам вычислительного процесса"
Гомель 2002
Реферат
Курсовая работа 25 страниц, 10 источников, 5 рисунков, 1 таблица
Ключевые слова: ИМИТАЦИОННАЯ МОДЕЛЬ, МЕТОД ВЕТВЕЙ И ГРАНИЦ, ПОЛУМАРКОВСКИЕ ПРОЦЕССЫ, ВЫЧИСЛИТЕЛЬНАЯ СИСТЕМА, ВЫЧИСЛИТЕЛЬНЫЙ ПРОЦЕСС, ПРОГРАММНЫЙ МОДУЛЬ, ГРАФ, МАТРИЦА ВЕРОЯТНОСТЕЙ, МЕТОД МОНТЕ-КАРЛО
Объект исследования: имитационная модель процесса обработки данных.
Предмет исследования: применение метода ветвей и границ в процессе обработки данных.
Цель курсовой работы: найти рациональный порядок следования запросов, который обеспечит максимальный критерий эффективности использования компонентов вычислительного процесса в вычислительной системе.
Задачами курсовой работы являются: изучить метод ветвей и границ и применить его к модели машинного моделирования, позволяющей найти такой порядок следования запросов, который обеспечит максимально быстрое выполнение вычислительного процесса.
Выводы: с помощью метода ветвей и границ удаётся построить такой порядок выполнения запросов, при котором время их обслуживания будет минимальным.
Содержание
Введение
1. Марковские процессы
2. Метод Монте-Карло
2.1 Общая характеристика метода Монте-Карло
2.2 Точность метода
3. Метод ветвей и границ
4. Построение оптимальной последовательности заданий на обработку в узле вычислительной системы
4.1 Формализация вычислительного процесса и рабочей нагрузки
4.2 Особенности организации имитационного эксперимента
4.3 Модификация последовательности решения задач в пакете по методу ветвей и границ
Заключение
Список источников
Введение
Выбором рабочей нагрузки под вычислительный процесс в вычислительных системах занимались многие исследователи. Однако все они оперировали интегральными характеристиками решения задач, не рассматривая при этом динамику использования ресурсов вычислительных систем во времени выполнения задач и пространстве параметров. Такой подход иногда приводил к существенной ошибке в оценке производительности системы в условиях, когда задания сильно конкурируют за ресурсы вычислительной системы. Это обстоятельство определило актуальность задачи адаптации рабочей нагрузки под возможности вычислительных систем в условиях, когда технология их обработки рассматривается на высоком уровне детализации. В данной работе будем исходить из следующих допущений:
1. Каждое задание вероятностным образом использует различные ресурсы вычислительного процесса, а сам вероятностный процесс является полумарковским.
2. Исследователю известны заранее характеристики полумарковского процесса, реализуемого каждым из заданий, или же имеются инструментальные средства для измерения этих характеристик.
3. Поток заданий постоянно используется на данной вычислительной системе и имеет практически неизменную структуру запросов ресурсов вычислительной системы, что позволяет говорить о принципиальной возможности нахождения такого порядка заданий, который является оптимальным при заданном составе ресурсов вычислительной системы.
1. Марковские процессы
Пусть имеется система, которая в произвольный момент времени tk может находиться в одном из состояний si,
Для дискретной цепи Маркова смены состояний процесса происходят в дискретные моменты времени ti с шагом
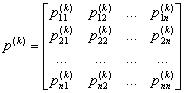
Эта матрица называется матрицей переходных вероятностей или матрицей переходов. Для неё справедливо выражение
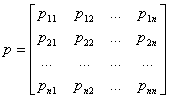
Вероятности перехода представляют собой важнейшие характеристики любой марковской цепи. Однако они по определению являются условными, и поэтому знание матрицы переходных вероятностей не полностью определяет цепь Маркова. Если отнести матрицу переходов к первому шагу, определяющему начало работы системы, то для исключения условностей необходимо задать ещё вероятности начальных состояний.
Вероятности начальных состояний
Матрица переходов даёт исчерпывающее представление о вероятностях возможных переходов за один шаг. Естественно возникает вопрос: как рассчитать вероятности того, что система, находящаяся в данный момент в состоянии si, переходит в состояние sj за r шагов. Матрица переходов за r шагов P(r) вычисляется как r-я степень матрицы перехода за один шаг P(r)=pr. Безусловные вероятности системы на r-м шаге определяются из выражений:
Различают цепи эргодические и поглощающие. Это различие основано на классификации состояний. Состояние si называется невозвратным, если существуют такие состояния sj (
Если выбрать такие состояния si и sj, что для них при некоторых r и q выполняется неравенство pij(r)>0, pji(r)>0, то они называются сообщающимися. Если sj сообщается с si, а si с sk, то sj сообщается с sk. Это обстоятельство позволяет разделить множество возвратных состояний на классы (подмножества) сообщающихся состояний. Состояния, принадлежащие к различным классам, не сообщаются между собой. Если множество возвратных состояний состоит из одного класса, то оно называется эргодическим. Существуют так называемые поглощающие состояния, например если si – поглощающее состояние, то pii=1, pij=0. Цепи Маркова, не содержащие возвратные множества и образующие эргодическое множество, называются эргодическими. Свойства и методы расчетов параметров поглощающих и эргодических цепей различны.
Для непрерывной цепи Маркова вводится понятие плотности вероятности перехода (интенсивность потока событий) как предела отношения вероятности перехода системы за время Δt из состояния i в состояние j к длине промежутка:
Если λij не зависит от t, то есть от того, в какой момент начинается Δt, то непрерывная цепь Маркова называется однородной, в противном случае она называется неоднородной.
Однородная цепь Маркова характеризуется тем, что все потоки, переводящие систему из одного состояния в другое, являются простейшими, то есть стационарными пуассоновскими потоками. При этом время непрерывного пребывания цепи в каждом состоянии распределено по экспоненциальному закону.
Для неоднородной цепи промежутки времени между соседними событиями распределены не по показательному закону.
Если непрерывная цепь Маркова является однородной и между любыми её двумя состояниями существует маршрут, то она эргодичная. Кроме того, если вероятности состояний системы pj не зависят от времени наблюдения системы и совпадают с её начальными вероятностями состояний
Отметим, что понятия «стационарность управляющих потоков» и «стационарный режим» совершенно разные и из первого не следует второе. Таким образом, однородная непрерывная цепь Маркова определяется начальным распределением вероятностей
Главное отличие полумарковского процесса от цепи Маркова состоит в отказе от требования, чтобы распределения времени пребывания в каждом состоянии подчинялись показательному закону. Обычно полумарковский процесс задаётся начальным распределением вероятностей
В моменты переходов из одного состояния в другое полумарковский процесс обладает марковским свойством. Если рассматривать полумарковский процесс только в моменты переходов, то получающаяся при этом марковская цепь с дискретным временем называется вложенной марковской цепью (так как она содержится в полумарковском процессе). Вложенная цепь имеет то же пространство состояний S и тот же вектор P(0) начального распределения вероятностей состояний, что и полумарковский процесс, а матрицей переходов вложенной цепи является матрица P=[pij] полумарковского процесса.
Для эргодических полумарковских процессов, как и для эргодических марковских цепей, характерно наличие стационарного режима.
2. Метод Монте-Карло
Различные методы и приборы для определения параметров и характеристик случайных процессов можно объединить в две группы. Первую группу составляют приборы для определения корреляционных функций (корреляторы), спектральных плотностей (спектрометры), математических ожиданий, дисперсий, законов распределения и прочих случайных процессов и величин.
Все приборы первой группы можно разделить на две подгруппы. Одни определяют характеристики записанных случайных сигналов за достаточно большое время, намного превышающее время реализации самого случайного процесса. Другие (они в последнее время вызывают наибольший интерес) позволяют получать характеристики случайного процесса оперативно, в такт с поступлением информации при натурных испытаниях новых систем управления, так как, пользуясь их показаниями, можно непосредственно изменять процесс управления и в ходе эксперимента наблюдать за результатами этих изменений.
Вторая группа содержит методы и приборы, предназначенные для исследования случайных процессов и главным образом систем управления, в которых присутствуют случайные сигналы, на универсальных цифровых и аналоговых вычислительных машинах. Иногда для таких исследований приходится создавать специализированные вычислительные машины цифрового, аналогового или чаще всего аналого-цифрового (гибридного) типа, так как существующие типовые машины не приспособлены для решения некоторых задач.
Широко применяется на практике метод Монте-Карло (метод статических испытаний). Его основная идея чрезвычайно проста и заключается по существу в математическом моделировании на вычислительной машине тех случайных процессов и преобразований с ними, которые имеют место в реальной системе управления. Этот метод в основном реализуется на цифровых и, реже, на аналоговых вычислительных машинах.
Можно утверждать, что метод Монте-Карло остаётся чистым методом моделирования случайных процессов, чистым математическим экспериментом, в известном смысле лишённым ограничений, свойственным другим методам. Рассмотрим данный метод применительно к решению различных задач управления.
2.1 Общая характеристика метода Монте-Карло
Как уже указывалось, идея метода Монте-Карло (или метода статистического моделирования) очень проста и заключается в том, что в вычислительной машине создаётся процесс преобразования цифровых данных, аналогичный реальному процессу. Вероятностные характеристики обоих процессов (реального и смоделированного) совпадают с какой-то точностью.
Допустим, необходимо вычислить математическое ожидание случайной величины X, подчиняющейся некоторому закону распределения F(x). Для этого в машине реализуют датчик случайных чисел, имеющий данное распределение F(x), и по формуле, которую легко запрограммировать, определяют оценку математического ожидания:
Каждое значение случайной величины xi представляется в машине двоичным числом, которое поступает с выхода датчика случайных чисел на сумматор. Для статистического моделирования рассматриваемой задачи требуется N-кратное повторение решения.
Рассмотрим ещё один пример. Производится десять независимых выстрелов по мишени. Вероятность попадания при одном выстреле задана и равна p. Требуется определить вероятность того, что число попаданий будет чётным, т.е. 0, 2, 4, 6, 8, 10. Вероятность того, что число попаданий будет 2k, равна:
откуда искомая вероятность
Если эта формула известна, то можно осуществить физический эксперимент, произведя несколько партий выстрелов (по десять в каждой) по реальной мишени. Но проще выполнить математический эксперимент на вычислительной машине следующим образом. Датчик случайных чисел выдаст в цифровом виде значение случайной величины ξ, подчиняющейся равномерному закону распределения в интервале [0,1]. Вероятность неравенства ξ<p равна p, т.е.
P {ξ<p}=p.

Для пояснения целесообразно обратиться к рис. 1, на котором весь набор случайных чисел представляется в виде точек отрезка [0,1]. Вероятность попадания случайной величины ξ, имеющей равномерное распределение в интервале [0,1], в интервал [0, p] (где
Различают две области применения метода Монте-Карло. Во-первых, для исследования на вычислительных машинах таких случайных явлений и процессов, как прохождение элементарных ядерных частиц (нейтронов, протонов и пр.) через вещество, системы массового обслуживания (телефонная сеть, система парикмахерских, система ПВО и пр.), надёжность сложных систем, в которых выход из строя элементов и устранения неисправностей являются случайными процессами, статистическое распознавание образов. Это – применение статистического моделирования к изучению так называемых вероятностных систем управления.
Этот метод широко применяется и для исследования дискретных систем управления, когда используются кибернетические модели в виде вероятностного графа (например, сетевое планирование с β-распределением времени выполнением работ) или вероятностного автомата.
Если динамика системы управления описывается дифференциальными или разностными уравнениями (случай детерминированных систем управления) и на систему, например угловую следящую систему радиолокационной станции воздействуют случайные сигналы, то статическое моделирование также позволяет получить необходимые точностные характеристики. В данном случае с успехом применяются как аналоговые, так и цифровые вычислительные машины. Однако, учитывая более широкое применение при статистическом моделировании цифровых машин, рассмотрим в данном разделе вопросы, связанные только с этим типом машин.
При решении алгебраических уравнений методом Монте-Карло число операций пропорционально числу уравнений, а при их решении детерминированными численными методами это число пропорционально кубу числа уравнений. Такое же приблизительно преимущество сохраняется вообще при выполнении различных вычислений с матрицами и особенно в операции обращения матрицы. Надо заметить, что универсальные вычислительные машины не приспособлены для матричных вычислений и метод Монте-Карло, применённый на этих машинах, лишь несколько улучшает процесс решения, но особенно преимущества вероятностного счёта проявляются при использовании специализированных вероятностных машин. Основной идеей, которая используется при решении детерминированных задач методом Монте-Карло, является замена детерминированной задачи эквивалентной статистической задачей, к которой можно применять этот метод. Естественно, что при такой замене вместо точного решения задачи получается приближённое решение, погрешность которого уменьшается с увеличением числа испытаний.
Эта идея используется в задачах дискретной оптимизации, которые возникают при управлении. Часто эти задачи сводятся к перебору большого числа вариантов, исчисляемого комбинаторными числами вида N=
При обработке больших массивов информации и управлении сверхбольшими системами, которые насчитывают свыше 100 тыс. компонентов (например, видов работ, промышленных изделий и пр.), встаёт задача укрупнения или эталонизации, т.е. сведения сверхбольшого массива к 100–1000 раз меньшему массиву эталонов. Это можно выполнить с помощью вероятностной модели. Считается, что каждый эталон может реализоваться или материализоваться в виде конкретного представителя случайным образом с законом вероятности, определяемым относительной частотой появления этого представителя. Вместо исходной детерминированной системы вводится эквивалентная вероятностная модель, которая легче поддаётся расчёту. Можно построить несколько уровней, строя эталоны эталонов. Во всех этих вероятностных моделях с успехом применяется метод Монте-Карло. Очевидно, что успех и точность статистического моделирования зависит в основном от качества последовательности случайных чисел и выбора оптимального алгоритма моделирования.
Задача получения случайных чисел обычно разбивается на две. Вначале получают последовательность случайных чисел, имеющих равномерное распределение в интервале [0,1]. Затем из неё получают последовательность случайных чисел, имеющих произвольный закон распределения. Один из способов такого преобразования состоит в использовании нелинейных преобразований. Пусть имеется случайная величина X, функция распределения вероятности для которой
Если y является функцией x, т.е. y=F(x), то

Полученная таким способом случайная величина X будет иметь функцию распределения F(x). Рассмотренная выше процедура может быть использована для графического способа получения случайных чисел, имеющих заданный закон распределения. Для этого на миллиметровой бумаге строится функция F(x) и вводится в рассмотрение другая случайная величина Y, которая связана со случайной величиной X соотношением (2) (рис. 2).
Так как любая функция распределения монотонно неубывающая, то
Отсюда следует, что величина Y имеет равномерный закон распределения в интервале [0,1], т. к. её функция распределения равна самой величине
Плотность распределения вероятности для Y
Для получения значения X берётся число из таблиц случайных чисел, имеющих равномерное распределение, которое откладывается на оси ординат (рис. 2), и на оси абсцисс считывается соответствующее число X. Повторив неоднократно эту процедуру, получим набор случайных чисел, имеющих закон распределения F(x). Таким образом, основная проблема заключается в получении равномерно распределённых в интервале [0,1] случайных чисел. Один из методов, который используется при физическом способе получения случайных чисел для ЭВМ, состоит в формировании дискретной случайной величины, которая может принимать только два значения: 0 или 1 с вероятностями

Далее будем рассматривать бесконечную последовательность z1, z2, z3,… как значения разрядов двоичного числа ξ* вида
Можно доказать, что случайная величина ξ*, заключённая в интервале [0,1], имеет равномерный закон распределения
В цифровой вычислительной машине имеется конечное число разрядов k. Поэтому максимальное количество несовпадающих между собой чисел равно 2k. В связи с этим в машине можно реализовать дискретную совокупность случайных чисел, т.е. конечное множество чисел, имеющих равномерный закон распределения. Такое распределение называется квазиравномерным. Возможные значения реализации дискретного псевдослучайного числа
Вероятность каждого значения (3) равна 2-k. Эти значения можно получить следующим образом
Случайная величина
Учитывая, что
и выражение для конечной суммы геометрической прогрессии
получаем:
Аналогично можно определить дисперсию величины
где
откуда
или, используя формулу (4), получаем:
Согласно формуле (5) оценка
где
Очевидно, что случайная величина ξ в соответствии с соотношением (3) может принимать значения
с вероятностью p=1/2k.
Математическое ожидание и дисперсию величины ξ можно получить из соотношений (5) и (6), если учесть (7). Действительно,
Отсюда получаем выражение для среднеквадратичного значения в виде
Напомним, что для равномерно распределённой в интервале [0,1] величины x имеем

Из формулы (8) следует, что при
Таблица 1
| k | 2 | 3 | 5 | 10 | 15 |
| σξ/ση | 1,29 | 1,14 | 1,030 | 1,001 | 1,00 |
На основании вышеизложенного задача получения совокупности квазиравномерных чисел сводится к получению последовательности независимых случайных величин zi (i=1,2,…, k), каждая из которых принимает значение 0 или 1 с вероятностью 1/2. Различают два способа получения совокупности этих величин: физический способ генерирования и алгоритмическое получение так называемых псевдослучайных чисел. В первом случае требуется специальная электронная приставка к цифровой вычислительной машине, во втором случае загружаются блоки машины.
При физическом генерировании чаще всего используются радиоактивные источники или шумящие электронные устройства. В первом случае радиоактивные частицы, излучаемые источником, поступают на счётчик частиц. Если показание счётчика чётное, то zi=1, если нечётное, то zi=0. Определим вероятность того, что zi=1. Число частиц k, которое испускается за время Δt, подчиняются закону Пуассона:
Вероятность чётного числа частиц
Таким образом, при больших λΔt вероятность P{Zi=1} близка к 1/2.
Второй способ получения случайных чисел zi более удобен и связан с собственными шумами электронных ламп. При усилении этих шумов получается напряжение u(t), которое является случайным процессом. Если брать его значения, достаточно отстоящие друг от друга, так чтобы они были некоррелированы, то величины u(ti) образуют последовательность независимых случайных величин. Обычно выбирают уровень отсечки a и полагают
причём уровень a следует выбрать так, чтобы
Также применяется более сложная логика образования чисел zi. В первом варианте используют два соседних значения u(ti) и u(ti+1), и величина Zi строится по такому правилу:

Если пара u(ti) – a и u(ti+1) – a одного знака, то берётся следующая пара. Требуется определить вероятность при заданной логике. Будем считать, что P {u(ti)>a}=W и постоянная для всех ti. Тогда вероятность события
u(ti) – a; u(ti+1) – a. (9)
Поэтому вероятность события A1Hv
P{A1Hv}=W (1-W) [W2+(1-W)2]v.
Это – вероятность того, что после v пар вида (9) появилось событие A1. Оно может появиться сразу с вероятностью W (1-W), оно может появиться и после одной пары вида (9) с вероятностью
W (1-W) [W2+(1+W)2]
и т.д. В результате
или
Отсюда следует, что если W=const, то логика обеспечивает хорошую последовательность случайных чисел. Второй способ формирования чисел zi состоит в следующем:

Пусть
W=P {u(ti)>a}=1/2+ξ.
Тогда
P{Zi=1}=2W (1-W)=1/2–2ξ2.
Чем меньше ξ, тем ближе вероятность P{Zi=1} к величине 1/2.
Для получения случайных чисел алгоритмическим путём с помощью специальных программ на вычислительной машине разработано большое количество методов. Так как на ЦВМ невозможно получить идеальную последовательность случайных чисел хотя бы потому, что на ней можно набрать конечное множество чисел, такие последовательности называются псевдослучайными. На самом деле повторяемость или периодичность в последовательности псевдослучайных чисел наступает значительно раньше и обусловливается спецификой алгоритма получения случайных чисел. Точные аналитические методы определения периодичности, как правило, отсутствуют, и величина периода последовательности псевдослучайных чисел определяется экспериментально на ЦВМ. Большинство алгоритмов получается эвристически и уточняется в процессе экспериментальной проверки. Рассмотрение начнём с так называемого метода усечений. Пусть задана произвольная случайная величина u, изменяющаяся в интервале [0,1], т.е.
un=u [mod 2-n], (10)
где u [mod 2-n] используется для определения операции получения остатка от деления числа u на 2-n. Можно доказать, что величины un в пределе при
По существу с помощью формулы (10) осуществляется усечение исходного числа со стороны старших разрядов. При оставлении далёких младших разрядов естественно исключается закономерность в числах и они более приближаются к случайным. Рассмотрим это на примере.
Пример 1. Пусть u = 0,10011101… = 1·1/2 + 0·1/22 + 0·1/23 + 1·1/24 + 1·1/25 + 1·1/26 + 0·1/27 + 1·1/28 + …
Выберем для простоты n=4. Тогда {u mod 2-4} = 0,1101…
Из рассмотренного свойства ясно, что существует большое количество алгоритмов получения псевдослучайных чисел. При этом после операции усечения со стороны младших разрядов применяется стандартная процедура нормализации числа в цифровой вычислительной машине. Так, если усечённое слева число не умещается по длине в машине, то производится усечение числа справа.
При проверке качества псевдослучайных чисел прежде всего интересуются длиной отрезка апериодичности и длиной периода (рис. 3). Под длиной отрезка апериодичности L понимается совокупность последовательно полученных случайных чисел α1, …, αL таких, что αi
Под длиной периода последовательности псевдослучайных чисел понимается T=L-i+1. Начиная с некоторого номера i числа будут периодически повторяться с этим периодом (рис. 3).

Как правило, эти два параметра (длины апериодичности и периода) определяются экспериментально. Качество совпадения закона распределения случайных чисел с равномерным законом проверяется с помощью критериев согласия.
2.2 Точность метода Монте-Карло
Метод Монте-Карло применяется там, где не требуется высокой точности. Например, если определяют вероятность поражения мишени при стрельбе, то разница между p1=0,8 и p2=0,805 несущественна. Обычно считается, что метод Монте-Карло позволяет получить точность примерно 0,01–0,05 максимального значения определяемой величины.
Получим некоторые рабочие формулы. Определим по методу Монте-Карло вероятность пребывания системы в некотором состоянии. Эта вероятность оценивается отношением
где M – число пребываний системы в этом состоянии в результате N моделирований. Учитывая выражение для дисперсии величины M/N
и неравенство Чебышёва
напишем

Величина
есть ни что иное, как ошибка моделирования по методу Монте-Карло. С помощью формулы (11) можно написать следующую формулу для величины (12):

или
где p0 – вероятность невыполнения этой оценки. С помощью частоты M/N может быть получена оценка математического ожидания mx некоторой случайной величины X. Ошибка этой оценки
находится с помощью соотношения

Отсюда видно, что ошибка моделирования находится в квадратичной зависимости от числа реализаций, т.е.
Пример 2. Допустим, что определяется математическое ожидание ошибки x поражения мишени. Процесс стрельбы и поражения моделируется на ЦВМ по методу Монте-Карло. Требуется точность моделирования δ = 0,1 м с вероятностью p = 1-p0 = 0,9 при заданной дисперсии σx = 1 м. Необходимо определить количество моделирований N. По формуле (13) получаем:
При таком количестве реализаций обеспечивается δ=0,1 м с вероятностью p=0,9.
3. Метод ветвей и границ
Все комбинаторные методы решения задач целочисленного программирования основаны на той или иной идее направленного перебора вариантов, в результате которого путём перебора сокращенного числа допустимых решений отыскивается оптимальное решение. Перебор осуществляется с помощью определённого комплекса правил, которые позволяют исключать подмножества вариантов, не содержащие оптимальной точки.
В целом эти методы легче справляются с проблемой округлений, чем методы отсечения, как правило, не используют симплекс-процедуру линейного программирования и имеют более «простую арифметику» и более «сложную логику».
Основное содержание этих методов составляют динамическое программирование и совокупность способов решения, объединённых общим термином – метод «ветвей и границ».
Комплексный подход по схеме ветвлений объединяет целый ряд близких комбинаторных методов, как-то: метод ветвей и границ, метод последовательного конструирования, анализа и отсева вариантов и др. Общая идея метода крайне проста. Множество допустимых планов некоторым способом разбивается на подмножество. В свою очередь каждое из подмножеств по этому же или другому способу снова разбиваются на подмножества до тех пор, пока каждое подмножество не будет представлять собой точку в многомерном пространстве. В силу конечности наборов значений переменных дерево подмножеств (схема ветвления) конечно.
Построение схемы ветвления есть ни что иное, как формирование процедуры перебора. Перебор может осуществляться различными способами. Сечение исходной допустимой области G0 гиперплоскостью на части G11 и G12 с последующим разделением G11 на G21 и G22 представляет собой построение дерева ветвлений с соответствующими подмно-жествами, как это показано на рис. 4.
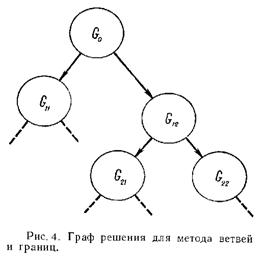
Возможность оценки образуемых подмножеств по наибольшему (наименьшему) значению для задач минимизации (максимизации) позволяет сократить перебор в силу того, что одно из подмножеств при выполнении определённых соотношений исключается и не нуждается в последующем анализе.
Понятно, что выбор оценок и схемы ветвления взаимосвязаны и трудно указать общие рекомендации по использованию на практике этого метода.
Схема ветвления иллюстрируется решением обобщённой задачи одномерного раскроя (пример 3) с конкретными числовыми данными.
Пример 3.
Имеются заготовки длиной a1=18, a2=16, a3=13. Разрезая их на части, но не склеивая, можно получать детали длинной b1=12, b2=10, b3=8, b4=6, b5=5, b6=4. Стоимость каждой детали известна и в условных единицах численно равна их длине. Перечисленные детали представляют собой «портфель заказов», который желательно обеспечить в первую очередь. В том случае, если это невозможно, максимизируется стоимость получаемых деталей из заданной номенклатуры. Если же портфель заказов обеспечивается, необходимо максимизировать стоимость дополнительной продукции.
Величину 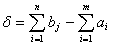
будем называть дефицитом. Отрицательность дефицита ещё не означает существование варианта раскроя, при положительном дефиците раскрой невозможен. Это свойство может быть использовано для указания перспективности варианта. Так, если заготовка a2 раскраивается на b2 и b5, то независимо от комбинаций остальных отрезков раскрой невыполним, поскольку для оставшихся отрезков дефицит положителен.
Первые этапы приводимой ниже схемы ветвления, использующей комбинаторные отношения подмножеств вариантов, показаны на рис. 5. На первом этапе формируются разбиения первой группы отрезков (заготовок) на вторую группу (деталей) независимо от того, какой именно отрезок первой группы разрезается. Количество ветвей первого этапа можно вычислить лишь по рекуррентным соотношениям. Смысл подмножества {1, 2, 3} заключается в том, что один из отрезков первой группы в результате раскроя даёт один отрезок второй группы, один из оставшихся отрезков первой группы раскраивается на два отрезка второй группы из числа оставшихся и, наконец, последний отрезок первой группы делится на три части, образуя три отрезка второй группы. На втором этапе формируются все перестановки (с учётом порядка) элементов первого этапа. Скажем, вариант {2, 1, 3} означает, что именно первый элемент первой группы a1 разрезается на две части и т.д.

Очередной этап ветвления образуется фиксацией отрезков второй группы при указанном на предыдущем этапе числе частей, на которое разрезается первый элемент. Другими словами, формируем сочетания по числу разделений первого элемента первого множества на число элементов второго множества. В дальнейшем фиксируем отрезки второй группы при втором элементе первой группы и, наконец, при оставшемся элементе первой группы получаем варианты раскроя, всего 447 вариантов. В подробно описанной схеме ветвления в отличие от часто применяемых ни на одном этапе не используется конкретный числовой материал. Рекомендуется построить для этого же примера иную схему ветвления, начиная с третьего этапа, по следующему признаку: отрезки второй группы фиксируются при элементе первой группы, разрезаемом на меньшее число частей. Затем надо сравнить схемы. Нетрудно убедиться, что на каждом этапе ветвления осуществляется по регулярной процедуре, что позволяет запоминать лишь один вариант. Сравнение дефицитов предыдущего и последующего вариантов позволяет выделить перспективную ветвь. Окончательный результат имеет вид:
{(b2, b3), (b4, b5, b6), (b1)};
{(b1, b4), (b2, b5), (b3, b6)};
{(b1, b4), (b2, b6), (b3, b5)};
{(b1, b5), (b2, b4), (b3, b6)};
{(b2, b3), (b1, b6), (b4, b5)};
{(b1, b6), (b2, b4), (b3, b5)};
{(b2, b4), (b1, b6), (b3, b5)}.
Формально задачу можно было бы свести к общему виду линейной задачи целочисленного программирования, но такое сведение приведёт к значительному увеличению количества переменных и другим трудностям. Матрица коэффициентов при этом приобретает квазиблочный вид с неплотным заполнением её отличными от нуля элементами. Как правило, задачи многоиндексные с большим числом условий и сложной упорядоченностью рекомендуется решать по схеме ветвлений, используя специфику условий и ограничений.
Для задач дискретного типа этот метод получил наибольшее распространение в силу простоты и доступности самого метода и, кроме того, наиболее естественной формы описания систем условий и ограничений, являющихся, как правило, отправным пунктом построения дерева ветвления. По существу большинство оригинальных алгоритмов (Балаша-Фора-Мальгранжа, Черенина, Джефферсона, Хиллиера и др.) являются модификациями метода ветвей и границ с учётом специфики условий задачи.
4. Построение оптимальной последовательности заданий на обработку в узле вычислительной системы
4.1 Формализация вычислительного процесса и рабочей нагрузки
Узел вычислительной системы представляется в виде совокупности оборудования и программных компонент. Оборудование включает в себя: центральный процессор (CPU), внешнюю память (HDD), устройства ввода-вывода информации (IOI). Программными компонентами в вычислительной системе являются операционная система (OS) и множество задач, реализуемых по запросам рабочей нагрузки. Для моделирования рабочей нагрузки на узлах вычислительной системы необходимо провести декомпозицию каждого задания пакета рабочей нагрузки на отдельные программные модули (ПМj). Количество и типы программных модулей зависят от имеющегося состава оборудования и программных средств узла вычислительной системы. При этом можно выделить следующие типы программных модулей: ввода информации; обработки информации; реализация вычислений на центральном процессоре; вывода информации. Модуль обработки информации обращается к базе данных вычислительной системы.
В свою очередь реализация обращения к базе данных также имеет определённую структуру, характеризующуюся графом GBD связей модулей в базе данных (MDBk). Предполагается, что характер следования друг за другом модулей базы данных при выполнении запросов в модуле обработки информации также является полумарковским.
Поскольку реализация задания i из рабочей нагрузки характеризуется полумарковским процессом, то для определения характера этого процесса необходимо задать следующие характеристики:
· матрицу вероятности переходов i-го задания от одного (j-го) программного модуля к другому (l-му) программному модулю МРi=||Рijl||;
· матрицу, элементами которой являются функции распределения времени обработки задачи i в i-ом программном модуле при условии получения им управления от j-го программного модуля (MFi=||Fi(tjl)||);
· тип j-го программного модуля, с которого начинается полумарковский процесс задания i (jOi) и количество j-х программных модулей, реализуемых цепочкой j-х программных модулей (nOi).
Аналогичным способом определяются характеристики полумарковского процесса реализации обмена. В качестве исходной информации задаются:
· матрица вероятностей следования друг за другом MDBjk (Mqj=||qjks||);
· матрица, элементами которой являются функции распределения объёмов информации при выполнении MDBjs при условии того, что перед этим использовался модуль MDBjk (МФj=||Fj(Vobjs)||);
· тип MDBjk, с которого начинается обращение к базе данных (kO), и количество MDBjk, реализуемое при данном обращении j-го программного модуля к базе данных (mOj).
4.2 Особенности организации имитационного эксперимента
Динамика выполнения задач пользователей на оборудовании узла вычислительной системы отражается последовательностью j-х программных модулей и имеет вероятностный характер. Каждый j-й программный модуль узла захватывает ресурс центрального процессора, часть ресурса оперативной памяти (Voni) и обращается к внешней памяти (HDD). Ресурс центрального процессора всегда выделяется j-м программным модулем полностью. Распределение ресурса центрального процессора организует операционная система. Ресурс центрального процессора распределяется по всем j-м программным модулям и для его выделения на определённый квант времени (Δt) используется система управляющих сигналов, формируемых по заявкам, поступающим от j-х программных модулей. Внешняя память моделируется как место размещения базы данных, и поэтому выделение ресурса внешней памяти для j-х программных модулей осуществляется до завершения выполнения задания. Функционирование устройств информации ввода вывода и модуля вывода информации моделируются как обычные устройства массового обслуживания с дисциплиной FIFO.
Время, затраченное на выполнение задания i, обозначим через Тжi. Причём, в Тжi включается сумма времени обслуживания задачи i на всех устройствах вычислительной системы, а также сумма времён издержек выполнения запросов заданий из-за занятости требуемых ресурсов другими задачами.
Целью моделирования вычислительного процесса в вычислительных системах является минимизация 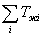
за счёт оптимизации порядка входа заданий рабочей нагрузки в вычислительной системе при неизменном составе ресурсов системы. Для получения оптимальной последовательности задач рабочей нагрузки необходимо знать: перечисленные ранее характеристики полумарковского представления процесса решения задач; ресурсные характеристики вычислительной системы; возможные реакции вычислительной системы на задания рабочей нагрузки с целью подсчёта времени обработки i-го задания в вычислительной системе.
Предполагается, что первые два условия задаются до постановки имитационного эксперимента. Поэтому ниже рассматриваются особенности моделирования вариантов обработки заданий в вычислительной системе.
Поскольку каждое задание использует ресурс вычислительной системы вероятностным образом, то для расчёта наиболее вероятного времени обработки узлом вычислительной системы i-го задания Tжi, а также коэффициентов загрузки центрального процессора (ηCPU) и внешней памяти (ηHDD) используется метод Монте-Карло. Количество реализаций (N) i-го задания i=1,…, n в вычислительной системе определяется из точности моделирования ( 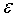
) для получения оценок вектора (Тжi, ηCPUi, ηHDDi). По окончании N реализаций имитационного эксперимента всех n заданий рабочей нагрузки получается матрица для каждого отклика (Тжi, ηCPUi, ηHDDi). Методика расчёта компонент этого вектора реализуется следующей последовательностью шагов.
Шаг 1. Нахождение времени решения задач (Тжi) и определение коэффициентов загрузки (ηCPU, ηHDDi) для различных уровней мультипрограммирования. Заметим, что обычно число уровней мультипрограммирования редко превышает величину 5, поэтому в нашем исследовании будем ориентироваться на максимальный уровень мультипрограммирования равный 5. Алгоритм реализации шага 1 основан на методе Монте-Карло для каждого уровня мультипрограммирования.
После N реализаций имитационного эксперимента с моделью вычислительного процесса для h-го уровня мультипрограммирования (h-й вариант вычислительного процесса, h=0,…, 5) по методу Монте-Карло будет сформировано три матрицы, компонентами которой будут пары значений:
M1ih=||(MTжih, DTжih)||; M2ih=||(MηCPUih, DCPUih)||; M3ih=||(MηHDDih, DηHDDih)||.
Шаг 2. По матрицам M1ih, M2ih, M3ih для h-го уровня мультипрограммирования определяют математические ожидания и дисперсии вычислений каждого из откликов: времени решения всего пакета (МТПАКh, МТПАКh); общей загрузки центрального процессора (MηHDDh, DηHDDh); общей загрузки внешней памяти (MηHDDh, DηHDDh) по формулам:
MYПАКh= 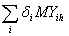
, DYПАКh= 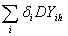
,
где 0 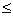
δi 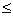
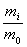
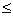
1 – весовой коэффициент задач i-го типа в пакете;
m0 – общее число задач в пакете;
mi – количество задач i-го типа в пакете;
YПАКh – отклик, содержание которого соответствует одной из характеристик вычислительного процесса в вычислительной системе (Тж, ηCPU, ηHDD).
4.3 Модификация последовательности решения задач в пакете по методу ветвей и границ
Описанная выше структура пакета рабочей нагрузки позволяет выделить следующие возможные случаи количества типов заданий.
1. Все задания пакета рабочей нагрузки имеют один и тот же тип (i=1).
2. В пакете имеются различные типы заданий и количество типов (1<i<m0).
3. Все задания пакета имеют различные типы (i=m0).
Наибольший интерес для исследования поиска оптимального расположения задач в пакете рабочей нагрузки представляет третий случай. Поэтому рассмотрим применение метода ветвей и границ для этого случая.
Шаг 0. Вычисляется общее время обработки всего ещё не упорядоченного пакета Tξ(STR).
Шаг 1. Размерность множества STR равна n (|STR| = n). На первом уровне ветвления вычисляются оценки Tξ(STRi1), i=1,…, n. Они вычисляются при условии, что i-е задание начинает обрабатываться первым, а оставшиеся n-1 заданий входят в расписание по мере возрастания Тжi. Среди этих оценок выбирается оценка с наименьшим Tξ(STRi1) и соответствующее i-е задание (i1) вставляется в расписание первым. При этом остальные оценки отбрасываются и соответствующие им порядки следования задач заданий считаются заведомо неоптимальными.
Шаг 2. Размерность массива STR равна n-1 (|STR| = n-1). Этот уровень ветвления осуществляется при условии, что одно из заданий i (i1) уже вставлено в расписание для обработки первым. Для остальных n-1 заданий, ещё не вставленных в расписание, вычисляются оценки Tξ(STRi2), i=1,…, n-1, при условии, что задание i загружается для обработки вторым, а оставшиеся n-2 заданий входят в расписание по мере возрастания Тжi. Среди этих оценок выбирается оценка с наименьшим Tξ(STRi2) и соответствующее i-е задание (i2) вставляется в расписание вторым. При этом остальные оценки отбрасываются и соответствующие им порядки следования задач заданий считаются заведомо неоптимальными. В результате второго шага в оптимальное расписание будут вставлены уже два задания.
Шаг k (k>2). Размерность массива STR равна n-k+1 (|STR| = n-k+1). Этот уровень ветвления осуществляется при условии, что k-1 задание уже вставлено в расписание. Для остальных n-k+1 заданий, ещё не вставленных в расписание, вычисляются оценки Tξ(STRik), i=1,…, n-k+1. Среди этих оценок выбирается оценка с наименьшим Tξ(STRik) и соответствующее i-е задание (ik) вставляется в расписание k-ым. При этом остальные оценки отбрасываются и соответствующие им порядки следования задач заданий считаются заведомо неоптимальными. В результате k-го шага в оптимальное расписание будут вставлены уже k заданий.
Шаг n. Размерность множества STR равна 1 (|STR| = 1). На этом шаге осталось только одно задание, не вставленное в расписание. Оно вставляется в расписание последним, и вычисляется оценка Tξ(STRin), i=1, которая и будет итоговой оценкой (временем) обработки заданий пакета рабочей нагрузки при соответствующем ей расписании.
После получения оптимальной последовательности порядка задач с помощью метода ветвей и границ необходимо сравнить это время обработки пакета со временем, полученным при начальном расположении заданий в пакете рабочей нагрузки.
Заключение
Проблема адаптации рабочей нагрузки к параметрам вычислительного процесса представляется актуальной из-за необходимости повышения эффективности использования ресурсов вычислительной системы и качества обслуживания запросов пользователя. Кроме того, на практике зачастую непрерывно меняются и состав, и структура рабочей нагрузки, что усложняет ситуацию выбора оптимального варианта вычислительного процесса.
Изучив и проанализировав ряд научных статей, посвящённых данной проблеме, следует отметить, что наиболее простым и распространённым способом её решения является метод ветвей и границ. Было установлено, что большинство существующих оригинальных алгоритмов являются модификациями данного метода. Впервые метод ветвей и границ был предложен Лендом и Дойгом в 1960 году для решения общей задачи целочисленного линейного программирования. Интерес к этому методу и фактически его «второе рождение» связано с работой Литтла, Мурти, Суини и Кэрела, посвященной задаче комивояжера. Начиная с этого момента, появилось большое число работ, посвященных методу ветвей и границ и различным его модификациям.
Можно утверждать, что проблема адаптации рабочей нагрузки будет оставаться актуальной и в ближайшем будущем в связи с тем, что её можно решать и в условиях локальных вычислительных сетей.
Таким образом, рассмотренное применение метода ветвей и границ к построению оптимальной последовательности заданий на обработку в вычислительной системе позволяет говорить о возможной эффективности привлечения этого метода к такому типу задач.
Список источников
1. Галиев Р.С. Экспериментальные методы исследования вычислительного процесса ЕС ЭВМ. – Дис., Гомель, 1987.
2. Демиденко О.М., Максимей И.В., Имитационное моделирование взаимодействия процессов в вычислительных системах. – Мн.: Белорусская наука, 2000.
3. Корбут А.А., Финкельштейн Ю.Ю., Дискретное программирование. – М.: Наука, 1969.
4. Максимей И.В., Серегина В.С. Задачи и модели исследования операций. Часть 2. – Гомель, 1999.
5. Максимей И.В. Имитационное моделирование на ЭВМ. – М.: Радио и связь, 1988.
6. Грек В.В., Максимей И.В. Стандартизация и метрология систем обработки данных. – Мн.: Высшая школа, 1994.
7. Бышик Т.П., Маслович С.Ф., Мережа В.Л. О построении оптимальной последовательности заданий на обработку в узле ЛВС // Известия Гомельского государственного университета имени Ф. Скорины. – 2002. – №6 (15) – С. 7–9.
8. Кузин Л.Т. Основы кибернетики. Том 1. – М.: Энергия, 1973.
9. Land A.H., and Doig A.G. An automatic method of solving discrete programming problems. Econometrica. v28 (1960), pp.497–520.
10. Little J.D.C., Murty K.G., Sweeney D.W., and Karel C. An algorithm for the traveling salesman problem. Operations Research. v11 (1963), pp. 972–989.
Комплексный подход по схеме ветвлений объединяет целый ряд близких комбинаторных методов, как-то: метод ветвей и границ, метод последовательного конструирования, анализа и отсева вариантов и др. Общая идея метода крайне проста. Множество допустимых планов некоторым способом разбивается на подмножество. В свою очередь каждое из подмножеств по этому же или другому способу снова разбиваются на подмножества до тех пор, пока каждое подмножество не будет представлять собой точку в многомерном пространстве. В силу конечности наборов значений переменных дерево подмножеств (схема ветвления) конечно.
Построение схемы ветвления есть ни что иное, как формирование процедуры перебора. Перебор может осуществляться различными способами. Сечение исходной допустимой области G0 гиперплоскостью на части G11 и G12 с последующим разделением G11 на G21 и G22 представляет собой построение дерева ветвлений с соответствующими подмно-жествами, как это показано на рис. 4.

Возможность оценки образуемых подмножеств по наибольшему (наименьшему) значению для задач минимизации (максимизации) позволяет сократить перебор в силу того, что одно из подмножеств при выполнении определённых соотношений исключается и не нуждается в последующем анализе.
Понятно, что выбор оценок и схемы ветвления взаимосвязаны и трудно указать общие рекомендации по использованию на практике этого метода.
Схема ветвления иллюстрируется решением обобщённой задачи одномерного раскроя (пример 3) с конкретными числовыми данными.
Пример 3.
Имеются заготовки длиной a1=18, a2=16, a3=13. Разрезая их на части, но не склеивая, можно получать детали длинной b1=12, b2=10, b3=8, b4=6, b5=5, b6=4. Стоимость каждой детали известна и в условных единицах численно равна их длине. Перечисленные детали представляют собой «портфель заказов», который желательно обеспечить в первую очередь. В том случае, если это невозможно, максимизируется стоимость получаемых деталей из заданной номенклатуры. Если же портфель заказов обеспечивается, необходимо максимизировать стоимость дополнительной продукции.
Величину
Первые этапы приводимой ниже схемы ветвления, использующей комбинаторные отношения подмножеств вариантов, показаны на рис. 5. На первом этапе формируются разбиения первой группы отрезков (заготовок) на вторую группу (деталей) независимо от того, какой именно отрезок первой группы разрезается. Количество ветвей первого этапа можно вычислить лишь по рекуррентным соотношениям. Смысл подмножества {1, 2, 3} заключается в том, что один из отрезков первой группы в результате раскроя даёт один отрезок второй группы, один из оставшихся отрезков первой группы раскраивается на два отрезка второй группы из числа оставшихся и, наконец, последний отрезок первой группы делится на три части, образуя три отрезка второй группы. На втором этапе формируются все перестановки (с учётом порядка) элементов первого этапа. Скажем, вариант {2, 1, 3} означает, что именно первый элемент первой группы a1 разрезается на две части и т.д.

Очередной этап ветвления образуется фиксацией отрезков второй группы при указанном на предыдущем этапе числе частей, на которое разрезается первый элемент. Другими словами, формируем сочетания по числу разделений первого элемента первого множества на число элементов второго множества. В дальнейшем фиксируем отрезки второй группы при втором элементе первой группы и, наконец, при оставшемся элементе первой группы получаем варианты раскроя, всего 447 вариантов. В подробно описанной схеме ветвления в отличие от часто применяемых ни на одном этапе не используется конкретный числовой материал. Рекомендуется построить для этого же примера иную схему ветвления, начиная с третьего этапа, по следующему признаку: отрезки второй группы фиксируются при элементе первой группы, разрезаемом на меньшее число частей. Затем надо сравнить схемы. Нетрудно убедиться, что на каждом этапе ветвления осуществляется по регулярной процедуре, что позволяет запоминать лишь один вариант. Сравнение дефицитов предыдущего и последующего вариантов позволяет выделить перспективную ветвь. Окончательный результат имеет вид:
{(b2, b3), (b4, b5, b6), (b1)};
{(b1, b4), (b2, b5), (b3, b6)};
{(b1, b4), (b2, b6), (b3, b5)};
{(b1, b5), (b2, b4), (b3, b6)};
{(b2, b3), (b1, b6), (b4, b5)};
{(b1, b6), (b2, b4), (b3, b5)};
{(b2, b4), (b1, b6), (b3, b5)}.
Формально задачу можно было бы свести к общему виду линейной задачи целочисленного программирования, но такое сведение приведёт к значительному увеличению количества переменных и другим трудностям. Матрица коэффициентов при этом приобретает квазиблочный вид с неплотным заполнением её отличными от нуля элементами. Как правило, задачи многоиндексные с большим числом условий и сложной упорядоченностью рекомендуется решать по схеме ветвлений, используя специфику условий и ограничений.
Для задач дискретного типа этот метод получил наибольшее распространение в силу простоты и доступности самого метода и, кроме того, наиболее естественной формы описания систем условий и ограничений, являющихся, как правило, отправным пунктом построения дерева ветвления. По существу большинство оригинальных алгоритмов (Балаша-Фора-Мальгранжа, Черенина, Джефферсона, Хиллиера и др.) являются модификациями метода ветвей и границ с учётом специфики условий задачи.
4. Построение оптимальной последовательности заданий на обработку в узле вычислительной системы
4.1 Формализация вычислительного процесса и рабочей нагрузки
Узел вычислительной системы представляется в виде совокупности оборудования и программных компонент. Оборудование включает в себя: центральный процессор (CPU), внешнюю память (HDD), устройства ввода-вывода информации (IOI). Программными компонентами в вычислительной системе являются операционная система (OS) и множество задач, реализуемых по запросам рабочей нагрузки. Для моделирования рабочей нагрузки на узлах вычислительной системы необходимо провести декомпозицию каждого задания пакета рабочей нагрузки на отдельные программные модули (ПМj). Количество и типы программных модулей зависят от имеющегося состава оборудования и программных средств узла вычислительной системы. При этом можно выделить следующие типы программных модулей: ввода информации; обработки информации; реализация вычислений на центральном процессоре; вывода информации. Модуль обработки информации обращается к базе данных вычислительной системы.
В свою очередь реализация обращения к базе данных также имеет определённую структуру, характеризующуюся графом GBD связей модулей в базе данных (MDBk). Предполагается, что характер следования друг за другом модулей базы данных при выполнении запросов в модуле обработки информации также является полумарковским.
Поскольку реализация задания i из рабочей нагрузки характеризуется полумарковским процессом, то для определения характера этого процесса необходимо задать следующие характеристики:
· матрицу вероятности переходов i-го задания от одного (j-го) программного модуля к другому (l-му) программному модулю МРi=||Рijl||;
· матрицу, элементами которой являются функции распределения времени обработки задачи i в i-ом программном модуле при условии получения им управления от j-го программного модуля (MFi=||Fi(tjl)||);
· тип j-го программного модуля, с которого начинается полумарковский процесс задания i (jOi) и количество j-х программных модулей, реализуемых цепочкой j-х программных модулей (nOi).
Аналогичным способом определяются характеристики полумарковского процесса реализации обмена. В качестве исходной информации задаются:
· матрица вероятностей следования друг за другом MDBjk (Mqj=||qjks||);
· матрица, элементами которой являются функции распределения объёмов информации при выполнении MDBjs при условии того, что перед этим использовался модуль MDBjk (МФj=||Fj(Vobjs)||);
· тип MDBjk, с которого начинается обращение к базе данных (kO), и количество MDBjk, реализуемое при данном обращении j-го программного модуля к базе данных (mOj).
4.2 Особенности организации имитационного эксперимента
Динамика выполнения задач пользователей на оборудовании узла вычислительной системы отражается последовательностью j-х программных модулей и имеет вероятностный характер. Каждый j-й программный модуль узла захватывает ресурс центрального процессора, часть ресурса оперативной памяти (Voni) и обращается к внешней памяти (HDD). Ресурс центрального процессора всегда выделяется j-м программным модулем полностью. Распределение ресурса центрального процессора организует операционная система. Ресурс центрального процессора распределяется по всем j-м программным модулям и для его выделения на определённый квант времени (Δt) используется система управляющих сигналов, формируемых по заявкам, поступающим от j-х программных модулей. Внешняя память моделируется как место размещения базы данных, и поэтому выделение ресурса внешней памяти для j-х программных модулей осуществляется до завершения выполнения задания. Функционирование устройств информации ввода вывода и модуля вывода информации моделируются как обычные устройства массового обслуживания с дисциплиной FIFO.
Время, затраченное на выполнение задания i, обозначим через Тжi. Причём, в Тжi включается сумма времени обслуживания задачи i на всех устройствах вычислительной системы, а также сумма времён издержек выполнения запросов заданий из-за занятости требуемых ресурсов другими задачами.
Целью моделирования вычислительного процесса в вычислительных системах является минимизация
Предполагается, что первые два условия задаются до постановки имитационного эксперимента. Поэтому ниже рассматриваются особенности моделирования вариантов обработки заданий в вычислительной системе.
Поскольку каждое задание использует ресурс вычислительной системы вероятностным образом, то для расчёта наиболее вероятного времени обработки узлом вычислительной системы i-го задания Tжi, а также коэффициентов загрузки центрального процессора (ηCPU) и внешней памяти (ηHDD) используется метод Монте-Карло. Количество реализаций (N) i-го задания i=1,…, n в вычислительной системе определяется из точности моделирования (
Шаг 1. Нахождение времени решения задач (Тжi) и определение коэффициентов загрузки (ηCPU, ηHDDi) для различных уровней мультипрограммирования. Заметим, что обычно число уровней мультипрограммирования редко превышает величину 5, поэтому в нашем исследовании будем ориентироваться на максимальный уровень мультипрограммирования равный 5. Алгоритм реализации шага 1 основан на методе Монте-Карло для каждого уровня мультипрограммирования.
После N реализаций имитационного эксперимента с моделью вычислительного процесса для h-го уровня мультипрограммирования (h-й вариант вычислительного процесса, h=0,…, 5) по методу Монте-Карло будет сформировано три матрицы, компонентами которой будут пары значений:
M1ih=||(MTжih, DTжih)||; M2ih=||(MηCPUih, DCPUih)||; M3ih=||(MηHDDih, DηHDDih)||.
Шаг 2. По матрицам M1ih, M2ih, M3ih для h-го уровня мультипрограммирования определяют математические ожидания и дисперсии вычислений каждого из откликов: времени решения всего пакета (МТПАКh, МТПАКh); общей загрузки центрального процессора (MηHDDh, DηHDDh); общей загрузки внешней памяти (MηHDDh, DηHDDh) по формулам:
MYПАКh=
где 0
m0 – общее число задач в пакете;
mi – количество задач i-го типа в пакете;
YПАКh – отклик, содержание которого соответствует одной из характеристик вычислительного процесса в вычислительной системе (Тж, ηCPU, ηHDD).
4.3 Модификация последовательности решения задач в пакете по методу ветвей и границ
Описанная выше структура пакета рабочей нагрузки позволяет выделить следующие возможные случаи количества типов заданий.
1. Все задания пакета рабочей нагрузки имеют один и тот же тип (i=1).
2. В пакете имеются различные типы заданий и количество типов (1<i<m0).
3. Все задания пакета имеют различные типы (i=m0).
Наибольший интерес для исследования поиска оптимального расположения задач в пакете рабочей нагрузки представляет третий случай. Поэтому рассмотрим применение метода ветвей и границ для этого случая.
Шаг 0. Вычисляется общее время обработки всего ещё не упорядоченного пакета Tξ(STR).
Шаг 1. Размерность множества STR равна n (|STR| = n). На первом уровне ветвления вычисляются оценки Tξ(STRi1), i=1,…, n. Они вычисляются при условии, что i-е задание начинает обрабатываться первым, а оставшиеся n-1 заданий входят в расписание по мере возрастания Тжi. Среди этих оценок выбирается оценка с наименьшим Tξ(STRi1) и соответствующее i-е задание (i1) вставляется в расписание первым. При этом остальные оценки отбрасываются и соответствующие им порядки следования задач заданий считаются заведомо неоптимальными.
Шаг 2. Размерность массива STR равна n-1 (|STR| = n-1). Этот уровень ветвления осуществляется при условии, что одно из заданий i (i1) уже вставлено в расписание для обработки первым. Для остальных n-1 заданий, ещё не вставленных в расписание, вычисляются оценки Tξ(STRi2), i=1,…, n-1, при условии, что задание i загружается для обработки вторым, а оставшиеся n-2 заданий входят в расписание по мере возрастания Тжi. Среди этих оценок выбирается оценка с наименьшим Tξ(STRi2) и соответствующее i-е задание (i2) вставляется в расписание вторым. При этом остальные оценки отбрасываются и соответствующие им порядки следования задач заданий считаются заведомо неоптимальными. В результате второго шага в оптимальное расписание будут вставлены уже два задания.
Шаг k (k>2). Размерность массива STR равна n-k+1 (|STR| = n-k+1). Этот уровень ветвления осуществляется при условии, что k-1 задание уже вставлено в расписание. Для остальных n-k+1 заданий, ещё не вставленных в расписание, вычисляются оценки Tξ(STRik), i=1,…, n-k+1. Среди этих оценок выбирается оценка с наименьшим Tξ(STRik) и соответствующее i-е задание (ik) вставляется в расписание k-ым. При этом остальные оценки отбрасываются и соответствующие им порядки следования задач заданий считаются заведомо неоптимальными. В результате k-го шага в оптимальное расписание будут вставлены уже k заданий.
Шаг n. Размерность множества STR равна 1 (|STR| = 1). На этом шаге осталось только одно задание, не вставленное в расписание. Оно вставляется в расписание последним, и вычисляется оценка Tξ(STRin), i=1, которая и будет итоговой оценкой (временем) обработки заданий пакета рабочей нагрузки при соответствующем ей расписании.
После получения оптимальной последовательности порядка задач с помощью метода ветвей и границ необходимо сравнить это время обработки пакета со временем, полученным при начальном расположении заданий в пакете рабочей нагрузки.
Заключение
Проблема адаптации рабочей нагрузки к параметрам вычислительного процесса представляется актуальной из-за необходимости повышения эффективности использования ресурсов вычислительной системы и качества обслуживания запросов пользователя. Кроме того, на практике зачастую непрерывно меняются и состав, и структура рабочей нагрузки, что усложняет ситуацию выбора оптимального варианта вычислительного процесса.
Изучив и проанализировав ряд научных статей, посвящённых данной проблеме, следует отметить, что наиболее простым и распространённым способом её решения является метод ветвей и границ. Было установлено, что большинство существующих оригинальных алгоритмов являются модификациями данного метода. Впервые метод ветвей и границ был предложен Лендом и Дойгом в 1960 году для решения общей задачи целочисленного линейного программирования. Интерес к этому методу и фактически его «второе рождение» связано с работой Литтла, Мурти, Суини и Кэрела, посвященной задаче комивояжера. Начиная с этого момента, появилось большое число работ, посвященных методу ветвей и границ и различным его модификациям.
Можно утверждать, что проблема адаптации рабочей нагрузки будет оставаться актуальной и в ближайшем будущем в связи с тем, что её можно решать и в условиях локальных вычислительных сетей.
Таким образом, рассмотренное применение метода ветвей и границ к построению оптимальной последовательности заданий на обработку в вычислительной системе позволяет говорить о возможной эффективности привлечения этого метода к такому типу задач.
Список источников
1. Галиев Р.С. Экспериментальные методы исследования вычислительного процесса ЕС ЭВМ. – Дис., Гомель, 1987.
2. Демиденко О.М., Максимей И.В., Имитационное моделирование взаимодействия процессов в вычислительных системах. – Мн.: Белорусская наука, 2000.
3. Корбут А.А., Финкельштейн Ю.Ю., Дискретное программирование. – М.: Наука, 1969.
4. Максимей И.В., Серегина В.С. Задачи и модели исследования операций. Часть 2. – Гомель, 1999.
5. Максимей И.В. Имитационное моделирование на ЭВМ. – М.: Радио и связь, 1988.
6. Грек В.В., Максимей И.В. Стандартизация и метрология систем обработки данных. – Мн.: Высшая школа, 1994.
7. Бышик Т.П., Маслович С.Ф., Мережа В.Л. О построении оптимальной последовательности заданий на обработку в узле ЛВС // Известия Гомельского государственного университета имени Ф. Скорины. – 2002. – №6 (15) – С. 7–9.
8. Кузин Л.Т. Основы кибернетики. Том 1. – М.: Энергия, 1973.
9. Land A.H., and Doig A.G. An automatic method of solving discrete programming problems. Econometrica. v28 (1960), pp.497–520.
10. Little J.D.C., Murty K.G., Sweeney D.W., and Karel C. An algorithm for the traveling salesman problem. Operations Research. v11 (1963), pp. 972–989.