Лабораторная работа на тему Системы счисления и представления типов данных
Работа добавлена на сайт bukvasha.net: 2014-12-15Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Системы счисления и представления типов данных
Содержание
1. Позиционные системы счисления. 3
2. Переходы между основными системами счисления. 5
3. Основные 16‑ичные константы.. 5
4. Реализация целочисленных операций. 7
5. Представление отрицательных чисел. 8
6. Целочисленные типы данных в языке Си. 9
7. Вещественные типы данных в языке Си. 10
8. Кодирование символов. 12
9. Схемы алгоритмов. 14
1) шестидесятиричная (Древний Вавилон) – первая позиционная система счисления. До сих пор при измерении времени используется основание равное 60 (1 мин = 60 с, 1 ч = 60 мин);
2) двенадцатеричная система счисления (широкое распространение получила в XIX в. Число12 – «дюжина»: в сутках две дюжины часов. Счет не по пальцам. а по суставам пальцев. На каждом пальце руки, кроме большого, по 3 сустава – всего 12;
3) в настоящее время наиболее распространенными позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная.
Система счисления – способ записи (изображения) чисел. Символы, при помощи которых записывается число, называются цифрами. Алфавитом системы счисления называется совокупность различных цифр, используемых в позиционной системе счисления для записи чисел. Например: Алфавиты некоторых позиционных систем счисления. Десятичная система: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Двоичная система: {0, 1}
Восьмеричная система: {0, 1, 2, 3, 4, 5, 6, 7}
Шестнадцатеричная система: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}
Количество цифр в алфавите равно основанию системы счисления. Основанием позиционной системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.
Базисом позиционной системы счисления называется последовательность чисел, каждое из которых задает количественное значение или «вес» каждого разряда. Например: Базисы некоторых позиционных систем счисления.
Десятичная система: 100, 101, 102, 103, 104,…, 10n,…
Двоичная система: 20, 21, 22, 23, 24,…, 2n,…
Восьмеричная система: 80, 81, 82, 83, 84,…, 8n,…
Свернутой формой записи числа называется запись в виде
A=an-1an-2…a1a0.a-1…a-m
Именно такой формой записи чисел мы и пользуемся в повседневной жизни. Иначе свернутую форму записи называют естественной или цифровой.
Пример. Десятичное число 4718,63, двоичное число 1001,1, восьмеричное число 7764,1, шестнадцатеричное число 3АF16
Позиция цифры в числе называется разрядом: разряд возрастает справа налево, от младших к старшим, начиная с нуля. В позиционной системе счисления любое вещественное число в развернутой форме может быть представлено в следующем десятичном виде:
А = ± (an-1qn-1+an-2qn-2+ … +a0q0+a-1q-1+a-2q-2+ … +a-mq-m)
Здесь А – само число, q – основание системы счисления, ai – цифры, принадлежащие алфавиту данной системы счисления, n – число целых разрядов числа, m – число дробных разрядов числа. Развернутая форма записи числа – сумма произведений коэффициентов на степени основания системы счисления.
Пример. Десятичное число А10 = 4718,63 в развернутой форме запишется так:
А10 = 4·103 + 7·102 + 1·101 + 8·100 + 6·10-1 + 3·10-2
Двоичное число А2 = 1001,1 = 1·23 + 0·22 + 0·21 + 1·20 + 1·2-1
Восьмеричное число А8 = 7764,1 = 7·83 + 7·82 + 6·81 + 4·80 + 1·8-1
Шестнадцатеричное число А16 = 3АF16 = 3·162 + 10·161 + 15·160
2 ® 8. Двоичное число разбивается справа налево на триады (тройки цифр) и каждая триада заменяется на 8‑ичную цифру.
2 ® 16. Двоичное число разбивается справа налево на тетрады (четверки цифр) и каждая тетрада заменяется на 16‑ичную цифру.
8 ® 16 и 16 ® 8. Преобразование идет через двоичную СС.
Любое основание ® 10. Осуществляется по определению позиционной системы счисления.
10 ® 16. Имеется два способа преобразования.
1. Метод деления «уголком» строит результирующее 16‑ичное число от младших цифр к старшим. Для этого запоминаются целые остатки от деления исходного числа на 16, пока частное не станет равным 0. Записывая эти остатки в обратном порядке, получим ответ.
2. Метод «вычерпывания» состоит из нескольких итераций. На каждой итерации исходное число х оценивается снизу максимальной степенью m нового основания p = 16: х ≥ 16m. Затем определяем число r вхождений степени 16m в число х. Наконец, 16‑ичную цифру r записываем в результирующее число в разряд с номером m. Число x заменяем на меньшее число х – r · 16m. Если новое число х = 0, то алгоритм заканчивается, и остальные разряды результата заполняем нулями. В противном случае, переходим к следующей итерации.
Таблица 1. Шестнадцатеричные константы
Следующая таблица содержит популярные степени числа 2, а также их русские и английские названия.
Таблица 2. Степени числа 2
Последние строки кратных единиц были дополнены ГОСТом в 1991. Вычисления с числами, представленными в десятично-буквенном виде, можно осуществлять без перехода в десятичную СС. Например, 32 Т / 256 К = 245 / 218 = 227 = 128 М.
Таблицы 1 и 2 позволяют переводить 16‑ичные числа в десятично-буквенную запись без применения вычислительных средств. Например,
0х7D8A30 = 7·0x100000 + 13·0x10000 + 8·0x1000 + 10·0x100 + 3·16 = 7 M + 13·64 K + 8·4 K + 10·(K/4) + 48 = 7 M + 866,5 K + 48.
Отметим, что для десятично-буквенных чисел не выполняется дистрибутивный закон, то есть 1 М + 100 К не равен 1,1 М.
Определение 1. Логическим адресом ячейки памяти в ОЗУ с 20‑битной адресной шиной называется запись xxxx:yyyy, где хххх – шестнадцатеричный сегментный адрес, yyyy – шестнадцатеричное смещение. Физическим адресом этой ячейки называется число xxxx0 + yyyy.
Пример. Область кода программы расположена с ячейки 55А3:3000 по ячейку 9EEF:A0FF. Оценить размер области в килобайтах.
Решение. Физический адрес начала области 0х55А30 + 0х3000 = 0х58A30, конца области 0х9EEF0 + 0хA0FF = 0хA8FEF. Размер этой области равен 0хA8FEF – 0х58A30 + 1 = 0x505C0 = 5·64 К + 0·4 К + 10· (К/4) + 12·16= (320 + 2,5) К + 192 = 322,5 К + 192.
Определение 2. Нормализованным адресом ячейки памяти ОЗУ с 20‑битной адресной шиной называется запись xxxx:yyyy, где хххх – шестнадцатеричное число, yyyy – шестнадцатеричное смещение, не превосходящее размера параграфа, то есть из диапазона от 0 до 15.
Арифметические операции сложения, вычитания, умножения и деления с 16‑ичными числами осуществляются аналогично 10‑ичным числам, то есть «столбиком». Однако, имеются некоторые отличия.
Пример. Критерии деления 16‑ичного целого числа на 3 и на 5 выглядят одинаково: сумма цифр должна делится, соответственно, на 3 и на 5.
Пример. Оказывается в 16‑ичной СС 0x112 = 0x121, 0x122 = 0x144, 0x132 = 0x169.
Пример. Десятичное число 0,1 нельзя представить в виде конечной 2‑ичной дроби A = 0, a-1…a-m = a-12-1 + a-22-2 +… + a-m2-m. В противном случае, умножая равенство 0,1 = А на 10·2m, получим 2m = 10·(a-12m-1 +
a-22m-2 +… + a-m20). Последнее равенство невозможно, так как правая часть делится на 5, а левая – нет.
Этот код основан на простом соображении, что x + (-x) = 0 при сложении двоичных чисел столбиком. При этом единица, которая переходит из старшего 7‑го бита в несуществующий 8‑ой бит, пропадает. Например, для однобайтного числа x = 5 имеем
x = 5 = 0000 0101
+
– x = -5 = **** ****
____________________
0 = 0 = 0000 0000
Теперь конструируем число -5 = 1111 1011.
По умолчанию целые десятичные константы имеют тип int. Поэтому все целые числа должны содержаться в диапазоне -32758… 32757. Например, запись x = 100000 будет ошибочна независимо от типа переменной x. Для обозначения целой константы типа long используется суффикс l. Тогда инициализация long x = 100000l будет корректна.
Компилятор не проверяет выход результата целочисленного выражения за диапазон типа. Запись long x = 20000 + 20000 будет ошибочна, так как 40000 не содержится в диапазоне типа int. Это будет «хорошо скрытая» ошибка. Реально x будет содержать значение
40000 – 64 К. Запись long x = 20000l + 20000 будет уже корректна, так как результат будет иметь уже тип long.
Построим область корректного сложения для типа char.
char x, y, z;
x = y = 100;
z = x + y;
Нарисуем в системе координат (x, y) множество, для которого z будет содержать корректный ответ. Имеем систему
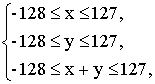
решением которой является шестиугольник.
SHAPE \* MERGEFORMAT
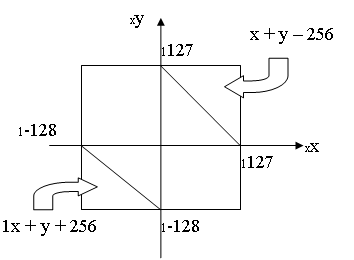
Рис. 1. Диапазон корректного сложения
Определение 3. Нормализованной формой ненулевого числа x называется запись x = M×10p, где M – мантисса, 0,1 £ ½ M ½ < 1, p – порядок числа х.
Нормализованная форма числа единственна.
Таблица 4. Вещественные типы данных
Определение 4. Машинным нулем для данного вещественного типа называется минимальное положительное число того же типа
m0 = min {x: x > 0}.
Определение 5. Машинным эпсилон для данного вещественного типа называется минимальное число того же типа, для которого 1 + x > 1
me = min {x: 1 + x > 1}.
Определение 6. Машинной бесконечностью для данного вещественного типа называется максимальное число того же типа
m¥ = max{x}.
По диапазону типа можно определить m0, m¥. Машинный эпсилон определяется размером мантиссы. Так, например, для типа float имеем
m0 = 3,4×10-38, m¥ = 3,4×1038, me » 10-8.
Определение 7. «Правым соседом» числа x данного вещественного типа назовем минимальное число y того же типа, для которого x < y
«Правый сосед» х = min {y: x < y}.
«Правый сосед» числа х больше самого х на величину равную
me × 10порядок числа х.
Приближенно можно считать, что «правый сосед» числа х » х + me × x.
Например, для типа float «правый сосед» числа 1010 » 1010 + 10-8 × 1010 = 1010 + 100.
Таким образом, вещественные числа данного типа расположены на числовой прямой неравномерно, чем больше числа, тем больше расстояние между соседними числами. Этот факт следует учитывать при организации циклов: шаг цикла должен быть больше, чем расстояние между соседними числами.
Параметры типа в таблице 4 связаны между собой.
Задача. Вещественный тип doom занимает 15 байт, под порядок отведено 30 бит. Определить остальные параметры этого типа.
Решение. Порядок занимает 30 бит, поэтому минимальное двоичное значение порядка равно -229. Для перевода этого числа к десятичному основанию решим показательное уравнение -229 = -10х. Логарифмируя по основанию 10, получаем х = 29 × lg2 » 29 × 0,3010 = 8,729. Таким образом, m0 равен 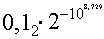
» 0,5 × 10-161290865,49 » 1,54 × 10-161290865.
Мантисса в двоичной системе счисления занимает 90 бит, из которых один бит определяет знак мантиссы. Так как первые знаки двоичной мантиссы равны 0,1 и всегда одинаковы, то под них память не отводится. Поэтому остальные 89 бит мантиссы занимают разряды с номерами от -2 до -90. «Правый сосед» единицы равен 0,100…0012 × 21, где последняя единица стоит в -90‑ом разряде. Тогда
Содержание
1. Позиционные системы счисления. 3
2. Переходы между основными системами счисления. 5
3. Основные 16‑ичные константы.. 5
4. Реализация целочисленных операций. 7
5. Представление отрицательных чисел. 8
6. Целочисленные типы данных в языке Си. 9
7. Вещественные типы данных в языке Си. 10
8. Кодирование символов. 12
9. Схемы алгоритмов. 14
1. Позиционные системы счисления
Позиционные системы счисления (СС) – это системы счисления, в которых количественный эквивалент каждой цифры зависит от ее положения (позиции) в записи числа. Например:1) шестидесятиричная (Древний Вавилон) – первая позиционная система счисления. До сих пор при измерении времени используется основание равное 60 (1 мин = 60 с, 1 ч = 60 мин);
2) двенадцатеричная система счисления (широкое распространение получила в XIX в. Число12 – «дюжина»: в сутках две дюжины часов. Счет не по пальцам. а по суставам пальцев. На каждом пальце руки, кроме большого, по 3 сустава – всего 12;
3) в настоящее время наиболее распространенными позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная.
Система счисления – способ записи (изображения) чисел. Символы, при помощи которых записывается число, называются цифрами. Алфавитом системы счисления называется совокупность различных цифр, используемых в позиционной системе счисления для записи чисел. Например: Алфавиты некоторых позиционных систем счисления. Десятичная система: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Двоичная система: {0, 1}
Восьмеричная система: {0, 1, 2, 3, 4, 5, 6, 7}
Шестнадцатеричная система: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}
Количество цифр в алфавите равно основанию системы счисления. Основанием позиционной системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.
Базисом позиционной системы счисления называется последовательность чисел, каждое из которых задает количественное значение или «вес» каждого разряда. Например: Базисы некоторых позиционных систем счисления.
Десятичная система: 100, 101, 102, 103, 104,…, 10n,…
Двоичная система: 20, 21, 22, 23, 24,…, 2n,…
Восьмеричная система: 80, 81, 82, 83, 84,…, 8n,…
Свернутой формой записи числа называется запись в виде
A=an-1an-2…a1a0.a-1…a-m
Именно такой формой записи чисел мы и пользуемся в повседневной жизни. Иначе свернутую форму записи называют естественной или цифровой.
Пример. Десятичное число 4718,63, двоичное число 1001,1, восьмеричное число 7764,1, шестнадцатеричное число 3АF16
Позиция цифры в числе называется разрядом: разряд возрастает справа налево, от младших к старшим, начиная с нуля. В позиционной системе счисления любое вещественное число в развернутой форме может быть представлено в следующем десятичном виде:
А = ± (an-1qn-1+an-2qn-2+ … +a0q0+a-1q-1+a-2q-2+ … +a-mq-m)
Здесь А – само число, q – основание системы счисления, ai – цифры, принадлежащие алфавиту данной системы счисления, n – число целых разрядов числа, m – число дробных разрядов числа. Развернутая форма записи числа – сумма произведений коэффициентов на степени основания системы счисления.
Пример. Десятичное число А10 = 4718,63 в развернутой форме запишется так:
А10 = 4·103 + 7·102 + 1·101 + 8·100 + 6·10-1 + 3·10-2
Двоичное число А2 = 1001,1 = 1·23 + 0·22 + 0·21 + 1·20 + 1·2-1
Восьмеричное число А8 = 7764,1 = 7·83 + 7·82 + 6·81 + 4·80 + 1·8-1
Шестнадцатеричное число А16 = 3АF16 = 3·162 + 10·161 + 15·160
2. Переходы между основными системами счисления
Основные СС имеют основания 2, 8,10, 16. Системы с основаниями 2, 8 и 16 являются родственными, так как их основания являются степенями двойки. Переходы между ними реализуются легко.2 ® 8. Двоичное число разбивается справа налево на триады (тройки цифр) и каждая триада заменяется на 8‑ичную цифру.
2 ® 16. Двоичное число разбивается справа налево на тетрады (четверки цифр) и каждая тетрада заменяется на 16‑ичную цифру.
8 ® 16 и 16 ® 8. Преобразование идет через двоичную СС.
Любое основание ® 10. Осуществляется по определению позиционной системы счисления.
10 ® 16. Имеется два способа преобразования.
1. Метод деления «уголком» строит результирующее 16‑ичное число от младших цифр к старшим. Для этого запоминаются целые остатки от деления исходного числа на 16, пока частное не станет равным 0. Записывая эти остатки в обратном порядке, получим ответ.
2. Метод «вычерпывания» состоит из нескольких итераций. На каждой итерации исходное число х оценивается снизу максимальной степенью m нового основания p = 16: х ≥ 16m. Затем определяем число r вхождений степени 16m в число х. Наконец, 16‑ичную цифру r записываем в результирующее число в разряд с номером m. Число x заменяем на меньшее число х – r · 16m. Если новое число х = 0, то алгоритм заканчивается, и остальные разряды результата заполняем нулями. В противном случае, переходим к следующей итерации.
3. Основные 16‑ичные константы
Большинство числовых констант, которые встречаются в компьютерной технике, являются круглыми шестнадцатеричными числами. Эти числа обычно записывают в десятично-буквенном виде, имеющем формат ab, где а – десятичное число, b – буква.Таблица 1. Шестнадцатеричные константы
| 16‑ичная константа | Десятично-буквенное значение | Примечания |
| 0х10 | 24 = 16 | Размер параграфа |
| 0х100 | 28 = 256 | Размер физического сектора |
| 0х200 | 512 | Размер кластера на дискете |
| 0х400 | 210 = 1024 = К | Килобайт |
| 0х1000 | 4 К | |
| 0х10000 | 64 К | Размер сегмента |
| 0хА0000 | 640 К | Верхняя граница ОЗУ для размещения исполняемого кода в DOS |
| 0х100000 | 220 = М | Мегабайт |
Таблица 2. Степени числа 2
| Показатель степени | Степень | Примечания |
| 0 | 1 | |
| 1 | 2 | |
| 2 | 4 | |
| 3 | 8 | |
| 4 | 16 | |
| 5 | 32 | |
| 6 | 64 | |
| 7 | 128 | |
| 8 | 256 | |
| 9 | 512 | |
| 10 | К = 1024 » 103, К | Килобайт, Kilobyte |
| 20 | М = К·К = К2 » 106, М | Мегабайт, Megabyte |
| 30 | Г = К3 » 109, G | Гигабайт, Gigabyte |
| 40 | Т = К4 = М2 » 1012, T | Терабайт, Terabyte |
| 50 | П » 1015, P | Петабайт, Petabyte |
| 60 | Э » 1018, E | Экзабайт, Exabyte |
| 70 | З » 1021, Z | Зетабайт, Zettabyte |
| 80 | Й » 1024, Y | Йотабайт, Yottabyte |
Таблицы 1 и 2 позволяют переводить 16‑ичные числа в десятично-буквенную запись без применения вычислительных средств. Например,
0х7D8A30 = 7·0x100000 + 13·0x10000 + 8·0x1000 + 10·0x100 + 3·16 = 7 M + 13·64 K + 8·4 K + 10·(K/4) + 48 = 7 M + 866,5 K + 48.
Отметим, что для десятично-буквенных чисел не выполняется дистрибутивный закон, то есть 1 М + 100 К не равен 1,1 М.
4. Реализация целочисленных операций
Представление чисел в компьютере осуществляется в двоичной СС. Однако для краткости записи чисел используют родственную 16‑ичную СС.Определение 1. Логическим адресом ячейки памяти в ОЗУ с 20‑битной адресной шиной называется запись xxxx:yyyy, где хххх – шестнадцатеричный сегментный адрес, yyyy – шестнадцатеричное смещение. Физическим адресом этой ячейки называется число xxxx0 + yyyy.
Пример. Область кода программы расположена с ячейки 55А3:3000 по ячейку 9EEF:A0FF. Оценить размер области в килобайтах.
Решение. Физический адрес начала области 0х55А30 + 0х3000 = 0х58A30, конца области 0х9EEF0 + 0хA0FF = 0хA8FEF. Размер этой области равен 0хA8FEF – 0х58A30 + 1 = 0x505C0 = 5·64 К + 0·4 К + 10· (К/4) + 12·16= (320 + 2,5) К + 192 = 322,5 К + 192.
Определение 2. Нормализованным адресом ячейки памяти ОЗУ с 20‑битной адресной шиной называется запись xxxx:yyyy, где хххх – шестнадцатеричное число, yyyy – шестнадцатеричное смещение, не превосходящее размера параграфа, то есть из диапазона от 0 до 15.
Арифметические операции сложения, вычитания, умножения и деления с 16‑ичными числами осуществляются аналогично 10‑ичным числам, то есть «столбиком». Однако, имеются некоторые отличия.
Пример. Критерии деления 16‑ичного целого числа на 3 и на 5 выглядят одинаково: сумма цифр должна делится, соответственно, на 3 и на 5.
Пример. Оказывается в 16‑ичной СС 0x112 = 0x121, 0x122 = 0x144, 0x132 = 0x169.
Пример. Десятичное число 0,1 нельзя представить в виде конечной 2‑ичной дроби A = 0, a-1…a-m = a-12-1 + a-22-2 +… + a-m2-m. В противном случае, умножая равенство 0,1 = А на 10·2m, получим 2m = 10·(a-12m-1 +
a-22m-2 +… + a-m20). Последнее равенство невозможно, так как правая часть делится на 5, а левая – нет.
5. Представление отрицательных чисел
Целые отрицательные числа хранятся в компьютере в двоичном «дополнительном» коде: положительное двоичное число необходимо побитово инвертировать и прибавить единицу.Этот код основан на простом соображении, что x + (-x) = 0 при сложении двоичных чисел столбиком. При этом единица, которая переходит из старшего 7‑го бита в несуществующий 8‑ой бит, пропадает. Например, для однобайтного числа x = 5 имеем
x = 5 = 0000 0101
+
– x = -5 = **** ****
____________________
0 = 0 = 0000 0000
Теперь конструируем число -5 = 1111 1011.
6. Целочисленные типы данных в языке Си
Таблица 3. Целочисленные типы данных| Название типа | Размер в байтах | Диапазон |
| unsigned char | 1 | 0 … 255, 0. 28 - 1 |
| char, signed char | 1 | -128 … 127, -27… 27-1 |
| unsigned int | 2 | 0. 65535, 0. 216 - 1, 0 … 64 K – 1 |
| int, signed int | 2 | -32758 … 32757, -215 … 215 - 1, -32 K… 32 K – 1 |
| unsigned long | 4 | 0… 232 - 1, 0… 4 M – 1 |
| long | 4 | -231… 231 - 1, 0… 4 M – 1 |
Компилятор не проверяет выход результата целочисленного выражения за диапазон типа. Запись long x = 20000 + 20000 будет ошибочна, так как 40000 не содержится в диапазоне типа int. Это будет «хорошо скрытая» ошибка. Реально x будет содержать значение
40000 – 64 К. Запись long x = 20000l + 20000 будет уже корректна, так как результат будет иметь уже тип long.
Построим область корректного сложения для типа char.
char x, y, z;
x = y = 100;
z = x + y;
Нарисуем в системе координат (x, y) множество, для которого z будет содержать корректный ответ. Имеем систему
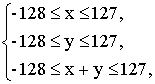
решением которой является шестиугольник.
SHAPE \* MERGEFORMAT
| 1127 |
| 1127 |
| 1-128 |
| 1-128 |
| x + y – 256 |
| 1x + y + 256 |
| xx |
| xy |

Рис. 1. Диапазон корректного сложения
7. Вещественные типы данных в языке Си
Вещественные типы всегда имеют знак.Определение 3. Нормализованной формой ненулевого числа x называется запись x = M×10p, где M – мантисса, 0,1 £ ½ M ½ < 1, p – порядок числа х.
Нормализованная форма числа единственна.
Таблица 4. Вещественные типы данных
| Название типа | Размер в байтах | Размер мантиссы в десятичных знаках | Размер порядка в битах | Диапазон |
| float | 4 | 7–8 | 8 | 3,4×10-38 … 3,4×1038 |
| double | 8 | 15–16 | 11 | 1,7×10-308… 1,7×10308 |
| long double | 10 | 19–20 | 15 | 3,4×10-4932… 1,1×104932 |
m0 = min {x: x > 0}.
Определение 5. Машинным эпсилон для данного вещественного типа называется минимальное число того же типа, для которого 1 + x > 1
me = min {x: 1 + x > 1}.
Определение 6. Машинной бесконечностью для данного вещественного типа называется максимальное число того же типа
m¥ = max{x}.
По диапазону типа можно определить m0, m¥. Машинный эпсилон определяется размером мантиссы. Так, например, для типа float имеем
m0 = 3,4×10-38, m¥ = 3,4×1038, me » 10-8.
Определение 7. «Правым соседом» числа x данного вещественного типа назовем минимальное число y того же типа, для которого x < y
«Правый сосед» х = min {y: x < y}.
«Правый сосед» числа х больше самого х на величину равную
me × 10порядок числа х.
Приближенно можно считать, что «правый сосед» числа х » х + me × x.
Например, для типа float «правый сосед» числа 1010 » 1010 + 10-8 × 1010 = 1010 + 100.
Таким образом, вещественные числа данного типа расположены на числовой прямой неравномерно, чем больше числа, тем больше расстояние между соседними числами. Этот факт следует учитывать при организации циклов: шаг цикла должен быть больше, чем расстояние между соседними числами.
Параметры типа в таблице 4 связаны между собой.
Задача. Вещественный тип doom занимает 15 байт, под порядок отведено 30 бит. Определить остальные параметры этого типа.
Решение. Порядок занимает 30 бит, поэтому минимальное двоичное значение порядка равно -229. Для перевода этого числа к десятичному основанию решим показательное уравнение -229 = -10х. Логарифмируя по основанию 10, получаем х = 29 × lg2 » 29 × 0,3010 = 8,729. Таким образом, m0 равен
Мантисса в двоичной системе счисления занимает 90 бит, из которых один бит определяет знак мантиссы. Так как первые знаки двоичной мантиссы равны 0,1 и всегда одинаковы, то под них память не отводится. Поэтому остальные 89 бит мантиссы занимают разряды с номерами от -2 до -90. «Правый сосед» единицы равен 0,100…0012 × 21, где последняя единица стоит в -90‑ом разряде. Тогда
me = 2-89 = 10-89 × lg(2) = 10-26,79 = 6,17 × 10-26
В ASCII‑таблице содержатся различные символы и соответствующие им коды. Например, символу ‘0’ соответствует код 0x30 = 48. Символы и строки хранятся в памяти в виде соответствующих кодов из ASCII‑таблицы. Например, строка «123» в памяти будет храниться в виде последовательности байт 0х31 0х32 0х33 0х00. Иногда строки, у которых 0 является признаком конца, называют asciiz‑строками.
Таблица 5. ASCII – таблица символов
Символу ‘b’ соответствует «ASCII‑код» 0x62. В десятичной системе это будет 98, а в двоичной – 01100010. Код символа ‘b’ вы можете посмотреть из ASCII‑таблицы. Таблицы символов для разных шрифтов можно найти с помощью программы Таблица Символов: Пуск – Стандартные – Системные утилиты – Таблица Символов).
В русской кодировочной странице 866 буква Ё имеет код 0xF0, а буква ё – код 0хF1.
В языке Си символьные константы обозначаются ‘\xxx’, где ххх – код этого символа, записанный в восьмеричной СС. Иначе говоря,
‘\xxx’ – это код символа, у которого код равен ххх.
Примеры. 1. Количество букв в английском алфавите равно
‘Z’ – ‘A’ + 1.
2. Количество букв в русском алфавите равно ‘Я’ – ‘А’ + 2.
Линии потока должны быть параллельны линиям внешней рамки схемы. Направления линий потока сверху вниз и слева направо принимают за основные и, если линии потока не имеют изломов, стрелками можно не обозначать. В остальных случаях направление линии потока обозначать стрелкой обязательно.
Сокращения слов и аббревиатуры, кроме стандартных и общепринятых, должны быть расшифрованы в нижней части поля схемы или в документе, к которому эта схема относится. Записи внутри символа должны быть представлены так, чтобы их можно было читать слева направо и сверху вниз, независимо от направления потока. (вид а должен быть прочитан как вид б).

Рис. 2. Эквивалентные фрагменты схемы алгоритма
Таблица 6. Соединитель
Таблица 7. Межстраничный соединитель
Таблица 8. Линии потока
Таблица 9. Возможные варианты отображения решения
Таблица 10
Символы в схемах алгоритмов
Размер a должен выбираться из ряда 10, 15, 20 мм. Допускается увеличивать размер a на число, кратное 5. Размер b равен 1,5 × a. При ручном выполнении схем алгоритмов и программ допускается устанавливать b равным 2 × a.
8. Кодирование символов
Для кодирования символов с помощью одного байта используется ASCII‑таблица (American Standard Code for Information Interchage)В ASCII‑таблице содержатся различные символы и соответствующие им коды. Например, символу ‘0’ соответствует код 0x30 = 48. Символы и строки хранятся в памяти в виде соответствующих кодов из ASCII‑таблицы. Например, строка «123» в памяти будет храниться в виде последовательности байт 0х31 0х32 0х33 0х00. Иногда строки, у которых 0 является признаком конца, называют asciiz‑строками.
Таблица 5. ASCII – таблица символов
| Основная таблица ASCII | Расширенная таблица ASCII |
 |  |
В русской кодировочной странице 866 буква Ё имеет код 0xF0, а буква ё – код 0хF1.
В языке Си символьные константы обозначаются ‘\xxx’, где ххх – код этого символа, записанный в восьмеричной СС. Иначе говоря,
‘\xxx’ – это код символа, у которого код равен ххх.
Примеры. 1. Количество букв в английском алфавите равно
‘Z’ – ‘A’ + 1.
2. Количество букв в русском алфавите равно ‘Я’ – ‘А’ + 2.
9. Схемы алгоритмов
Для облегчения вычерчивания и нахождения на схеме символов рекомендуется поле листа разбивать на зоны. Размеры зон устанавливают с учетом минимальных размеров символов, изображенных на данном листе. Допускается один символ размещать в двух и более зонах, если размер символа превышает размер зоны. Координаты зоны проставляют: по горизонтали – арабскими цифрами слева направо в верхней части листа; по вертикали – прописными буквами латинского алфавита сверху вниз в левой части листа. Координаты зон в виде сочетания букв и цифр присваивают символам, вписанным в поля этих зон, например: A1, A2, A3, B1, B2, B3 и т.д. Если поле листа не разбито на зоны, символам присваивают порядковые номера.Линии потока должны быть параллельны линиям внешней рамки схемы. Направления линий потока сверху вниз и слева направо принимают за основные и, если линии потока не имеют изломов, стрелками можно не обозначать. В остальных случаях направление линии потока обозначать стрелкой обязательно.
Сокращения слов и аббревиатуры, кроме стандартных и общепринятых, должны быть расшифрованы в нижней части поля схемы или в документе, к которому эта схема относится. Записи внутри символа должны быть представлены так, чтобы их можно было читать слева направо и сверху вниз, независимо от направления потока. (вид а должен быть прочитан как вид б).

Рис. 2. Эквивалентные фрагменты схемы алгоритма
Таблица 6. Соединитель
| Обозначение | Комментарии | Использование |
 | E5, B1, A, 5 – идентификаторы соединителей в виде: буквы и цифры (координаты зоны листа) | При большой насыщенности схемы символами отдельные линии потока между удаленными друг от друга символами допускается обрывать. При этом в конце (начале) обрыва должен быть помещен символ «Соединитель» |
 | буквы | |
 | цифры |
| Обозначение | Комментарии | Использование |
 | Первая строка внутри межстраничного соединителя определяет номер листа схемы, вторая – координату символа | а) связываемые линией потока символы находятся на разных листах |
 | A3 – определяет зону на данном листе, где расположен символ «Комментарий» 010E3 – определяет номер листа и зону расположения, связываемую с символом E3 | б) в случае связи некоторого символа со многими другими символами, расположенными на разных листах, на входе этого символа помещают один символ «Межстраничный соединитель», внутри которого на первой строке помещают знак #, а на второй строке – координаты символа «Комментарий». Внутри символа «Комментарий» указывают номера страниц и координаты символов, связанных с поясняемым символом |
| Обозначение | Комментарии | Использование |
 | Применяют для указания направления линии потока: можно без стрелки, если линия направлена слева направо и сверху вниз; со стрелкой – в остальных случаях | |
| | Излом линии потока под углом 90о | Обозначает изменение направлений линии потока |
 | Пересечение линий потока | Применяется в случае пересечения двух несвязанных линий потока |
 | Слияние линий потока. Место слияний линий потока обозначено точкой | Применяется в случае слияния линий потока, каждая из которых направлена к одному и тому же символу на схеме. Место слияния линий потока допускается обозначать точкой или цифрой 0. |
 | Место слияний линий потока обозначено цифрой 0 |
Таблица 9. Возможные варианты отображения решения
| Обозначение | Комментарии | Использование |
 | A = B, P ≥ 0 – условия решений; A, B, P – параметры | При числе исходов не более трех признак условия решения (Да, Нет, =, >, <) проставляют над каждой линией потока или справа от линии потока |
 | yi – условие i‑го исхода, 011T1, 016A3, 005B5, 015T4 – адреса исходов. Структура адреса имеет вид:  | При числе исходов более трех условие исхода проставляется в разрыве линии потока. Адрес исхода проставляется в продолжении условия исхода и отделяется от него пробелом |
 | B5 – знак, указывающий, что условия решения даются в виде таблицы или символа «Комментарий», расположенных на данном листе в зоне B5 | в символе «Соединитель» указывают координату зоны, куда должна помещаться таблица или символ «Комментарий» |
Символы в схемах алгоритмов
| Название символа | Обозначение | Использование |
| 1. Процесс |  | Выполнение операции или группы операций, в результате которых изменяется значение, форма представления или расположение данных |
| 2. Решение |  | Выбор направления выполнения алгоритма или программы в зависимости от некоторых переменных условий |
| 3. Модификация |  | Выполнение операций, меняющих команды, или группы команд, изменяющих программу |
| 4. Предопреде ленный процесс |  | Использование ранее созданных и отдельно описанных алгоритмов или программ |
| 5. Ручной ввод |  | Ввод данных вручную при помощи неавтономных устройства с клавиатурой, переключателей, кнопок |
| 6. Ввод-вывод |  | Преобразование данных в форму, пригодную для обработки (ввод) или отображения результатов обработки (вывод) |
| 7. Документ |  | Ввод-вывод данных, носителем которых служит бумага |
| 8. Файл |  | Представление организованных на основе общих признаков данных, характеризующих в совокупности некоторый объект обработки данных. Символ используется в сочетании с символами конкретных носителей данных, выполняющих функции ввода-вывода. |
| 9. Линия потока | | Указание последовательности связей между символами |
| 10. Соединитель |  | Указание связи между прерванными линиями потока, соединяющими символы |
| 11. Пуск-останов |  | Начало, конец, прерывание процесса обработки данных или выполнения программы |
| 12. Комментарий |  | Связь между элементом схемы и пояснением |
| 13. Межстраничный соединитель |  | Указание связи между разъединенными частями схем алгоритмов и программ, расположенных на разных листах |