Лекция на тему Численные методы 6
Работа добавлена на сайт bukvasha.net: 2014-12-16Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
ЛЕКЦИЯ №9
МНОГОЧЛЕНЫ ЧЕБЫШЕВА
1. Определение и свойства
2. Интерполяция по Чебышевским узлам
3. Многочлены равномерных приближений
4. Экономизация степенных рядов
Многочленом Чебышева n-ой степени называется функция
Tn(x)=cos (narccos) n=0,1,2 …,xÎ[-1;1] ; (9.1)
Докажем, что при любом n=0,1,2
n=0: T0(x)=cos0=1;
n=1: T1(x)=cos(arccos x)=x;
n=2: T2(x) =cos(2arccos x);
Обозначим α=arccosx
Tn(x)=cos2α ;
Tn+1(x)=cos((n+1)α) ;
Tn-1(x)=cos((n-1)α) ;
cos((n+1)α)+ cos((n-1)α)-2cos(2nα/ α)cos(2α/ α)=2 cosnα cosα;
Tn+1(x)+ Tn-1(x)=2 T1(x) Tn(x);
Tn+1(x)= 2xTn(x)- Tn-1(x); (9.2)
Свойства многочлена Чебышева:
1. Все функции Tn(x) являются многочленами при n=0,1,2,…
2. Степени этих многочленов возрастают с увеличением n, причем старший член Tn(x)=2n-1xn
3. Многочлены Tn(x) при четных n выражаются через четные функции , при нечетных n-через нечетные функции.
Проверим:
T2(x) =2х2-1
T3(x) =2х (2х2-1) =4х3-2х
T4(x) = 2х (4х3-3х)-2х2+1=23х4-3х2+1
4. На отрезке [-1;1] многочлен Tn(x) имеет ровно n различных действительных корней, которые рассчитываются по формуле:
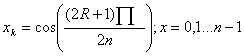
Докажем:
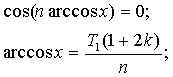
Так как arccosxÎ[0; Π];k=0,1,…n-1,чтобы туда попадал arcos
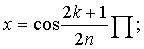
5. Корни многочлена Чебышева перемножаются, чередуются с точками их экстремума, причем максимум
Tn(x) на [-1;1] равен 1,т.е
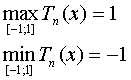
Для точек экстремума существует связь:
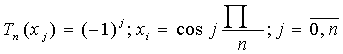
Введем нормированный многочлена Чебышева (старший коэффициент =1, перед х в максимальной степени)
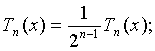
(9.3)
max | Рn*(x)| < max | T^n(x)|
[-1;1] [-1;1] Доказательство не нужно.
Остаточный член полинома Лагранжа
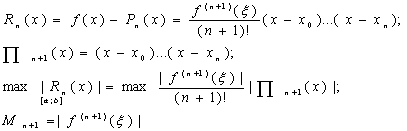
Необходимо минимизировать этот максимум, т.е необходимо найти такие узлы xk , 
которые минимизировали бы 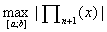
Сведем [a;b] к отрезку [-1;1]
Должна существовать связь хÎ[a;b] с t Î[-1;1]

Связь: x= Ct+D
C-коэффициент сжатия (растяжения, D-параллельный перенос)
Если t=1
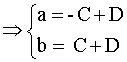
Если t=-1
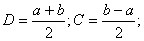
Тогда:
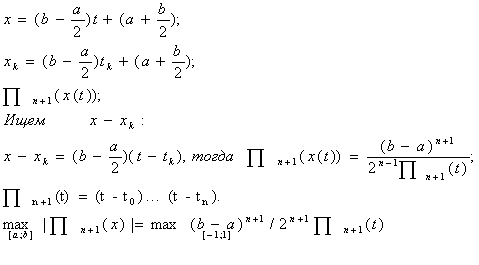
(9.4)
 Для того чтобы минимизировать (9.4), необходимо найти такие корни
Для того чтобы минимизировать (9.4), необходимо найти такие корни
tkÎ[-1;1], 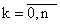
, при котором Πn+1(t) будет минимальным.
По теореме Чебышева полином Тn+1нормирован многочленом Чебышева, наименее отклонен от нуля на [-1;1], поэтому в качестве искомых корней необходимо взять корни многочлена Чебышева на [-1;1]
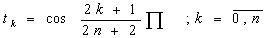
(рассмотрим полином n+1-ой степени)
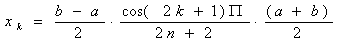
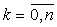
(9.5)
Узлы интерполяции, определим по формуле (9.5) обеспечивают min, max ошибку аппроксимации при помощи интерполяционных полиномов.
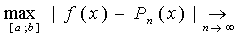
Т.е имеет место равномерная сходимость последовательности интерполяционного полинома Лагранжа функции f(x).
Теорема Вейерштрасса: для любой непрерывной функции f(x) на [a;b] найдется полином Qn(x), что |f(x)- Рn(x)| < ξ для любой ξ>0 , любое хÎ[a;b].
Т.е для любой f(x) непрерывной на [a;b],может быть построена аппроксимирующий наилучший полином, который минимизирует максимальное отклонение между f(x) и Qn(x). Такие полиномы называют многочленами наилучших равномерных приближений.
К сожалению, общий вид таких полиномов и способы построения не известны.
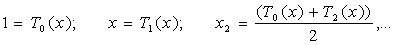
Такой процесс называется экономизацией степенного ряда.
Разложение по многочленам Чебышева имеет меньшую максимальную погрешность.
ЛЕКЦИЯ №10,11
ИНТЕРПОЛЯЦИОННЫЕ СПЛАЙНЫ
Когда интерполяционный отрезок [a;b] велик, нет, основания считать, функцию f(x) достаточно гладкой, на [a;b], то нельзя повышать точность аппроксимации за счет увеличения степени интерполяционного многочлена.
Связано это с тем, что у многочлена n-ой степени может быть n-1 точка экстремума. При n→∞ график многочлена начинает сильно колебаться

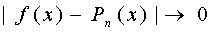
Такое явление называют феноменом Рунге.
Поэтому более перспективным является применение кусочно-полиномиальной аппроксимации, при которой аппроксимирующая функция составляется из отдельных многочленов (сплайнов). Каждый из которых (одинаковы и наибольшей степени) определен на своем участке отрезка [a;b].
Рассмотрим аппроксимацию кусочно-линейной функции (линейный сплайн).
Пусть f(x) задана таблично на [a;b], т. е определены некоторые узлы интерполяции a≤x0<x1<…<xn≤b
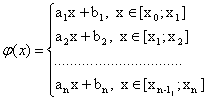
кусочно-линейная функция
Необходимо: φ(xi)=yi=f(xi), 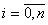
для приближения функции.
 Определим ai и bi.
Определим ai и bi.
x=x0: φ(x0)=f(x0)=y0 a1x0+b1=y0
 x=x1: φ(x1)=f(x1)=y1 a1x1+b1=y1
x=x1: φ(x1)=f(x1)=y1 a1x1+b1=y1
a2x1+b2=y1
x0 x1 x2
Получим систему:

а0x0+b1=y0 (решаем по отдельности каждую систему)
a2x1+b2=y1
a2x1+b2=y1
a2x2+b2=y2 (10.2)
anxn-1+bn=yn
anxn +bn= yn
Таким образом, получена система из 2n уравнений для поиска 2n неизвестных. Причем, система (10.2) образована из n систем линейных уравнений для 2-х неизвестных, каждая из которых может решаться независимо от остальных.
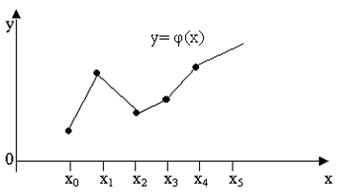
Кусочно-линейная функция φ(x) вида (10.1) внутри интервала (хi-1;xi), 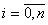
непрерывна и дифференцируема, а в точках xi, 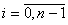
непрерывна, но не дифференцируема (в этих точках к графику функции невозможно построить касательную).

Чтобы функция приближала f(x) наложим ограничения φ(xi)=yi=f(xi), 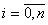
.
Общее число узлов 2n+1, если n-четное.
Для нахождения неизвестных коэффициентов ak,bk,ck необходимо построить 3m условий.
k=1
[x0;x2]
Обобщим, получим систему:
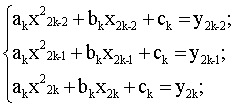
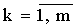
(10.4) 
Для нахождения неизвестных имеем 3m условий. При каждом значении 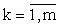
можем построить систему линейных уравнений для ak,bk,ck;
Решать ее можем независимо от остальных условий.
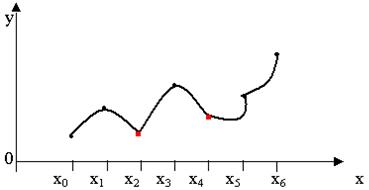
Кусочно- квадратичная φ(x) вида (10.3) внутри интервала (x2n-2-x2n), 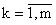
является непрерывной и дифференцируемой два раза, а в точках x2i 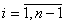
является непрерывной, но не дифференцируемой.
Определение Сплайна
Пусть на отрезке [a;b] задана некоторая система узлов a0≤x0< x1<…<xn ≤b
Сплайном Sn(x) называется функция, которая определена на [a;b], l раз непрерывна и дифференцируема на нем, при этом на каждом из отрезков
[хк-1; хк], к = 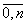
, представляет собой многочлен степени m.
Разность (m-1) называется дефектом Сплайна (показывает разность между степенью составляющих его многочленов и степенью гладкости общей функции).
Если сплайн построен по некоторой таблично заданной функции f(x) таким образом, что S(хi)= f(xi); xi , i= 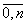
- узлы интерполяции, то сплайн называют интерполяционным. Узлы сплайна и узлы интерполяции функции могут не совпадать.
Очевидно, что функция (10.1) является интерполяционным сплайном степени 1, дефекта 1, а кусочно-квадратичная функция (10.3) является интерполяционным сплайном, степени 2, дефекта 2.
Интерполяционный сплайн степени 3, дефекта 1.
Дважды непрерывно – дифференцируемый – сплайн.
Пусть задана табличная функция на [a;b], причем a= χ0 ≤ χ1<…< χn=b (узлы сплайна совпадают с узлами интерполяции). Общий вид:
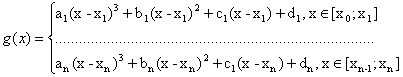
Условия:
1.) g(xi) = f(xi)=yi , i= 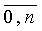
2.) g(x) = c2 (дважды дифференцируема) [a;b]
3.) – краевые условия
Для нахождения неизвестных коэффициентов введем функцию
gn(x) = ak(x-xk)3+ bk(x-xk)2+c1(x-xk)+dk, xÎ[ xk-1;xk] 
1.) g1(x0) = y0 , g1(x1) = y1 , g2(x2) = y2 ,… gn(xn) = yn
2.) первое условие (сплайн интерполяционный)
3.) 
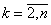
Краевые условия:
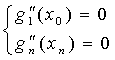
Таким образом, для нахождения 4n неизвестных мы построим 4n условий.
Теорема(10.1). Интерполяционный сплайн вида (10.5) для функции f(x) единственен.
Теорема(10.2). Пусть g(x)- интерполяционный сплайн степени 3 дефекта 1, построенный для функции f(x) С4 на отрезке [a;b], тогда для 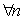
найдется такая константа C>0, что:
|f(x)- g(x)|<C 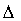
4, 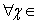
[a ;b],
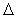
= max(xk-xk-1), 1≤ k ≤ n
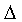
- максимальное расстояние между узлами интерполяции.
Линейный фильтр
Понятие линейного сплайна позволяет сформулировать подходы к построению линейных фильтров, предназначенных для устранения случайных ошибок в данных.
Обычно в ходе измерений на процесс фиксации данных оказывают влияние случайные помехи. Для того, чтобы уменьшить влияние этих помех на качество интерполяции осуществляют пересчет значений функции в узлах интерполяции по следующей формуле:
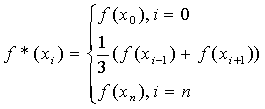
Квадратичный сплайн дефекта один
Узлы этого сплайна не совпадают с узлами интерполяции функции.
Пусть узлы интерполяции заданы на [a;b] 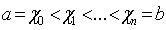
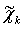
- узлы сплайна, f(xi)=yi

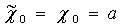
, 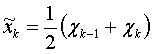
, 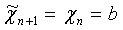
Для сплайна n+2 узлов
Квадратичный сплайн дефекта 1 имеет вид:
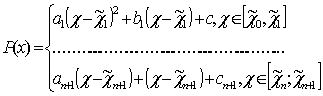
Условия:
1.) 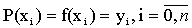
2.) P(x) Î C'[a;b], 
первая непрерывная производная во всех точках [a;b]
3.) Краевые условия:
P''(a)=A; P''(b)=B;
A и B- константы и желательно разные;
Чтобы построить сплайн необходимо найти 3n+3 неизвестных коэффициента. С этой целью сформирую функцию:
Pn(x)= ak 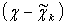
2+bn 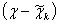
+ck 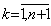
Условия:
1.) Pi+1=yi, i= 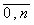
- n+1 условий
2.) Pk 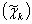
= Pk+1 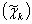
, 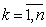
P'k 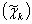
=P'k+1 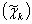
, 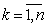
3.) P1 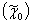
=A, P''n+1 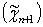
-B – краевые условия;
Теорема 11.1. Квадр. Сплайн дефекта один, вида (11.1) для функции существует и единственен.
Теорема 11.2. Пусть функция f(x) дважды непрерывна и дифференцируема на [a;b], а P(x)- сплайн вида (11.1), тогда для 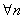
, (n- связано с числом узлов интерполяции) 
такие const c0, c1, c2; что для 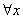
из [a;b] выполняются следующие неравенства:
| f(x)-P(x) | ≤ C0∆2
| f '(x)-P' (x)| 
≤C∆
| f ''(x)-P'' (x)| 
≤C2
где ∆- максимальное расстояние между узлами интерполяции, т.е ∆= max(xk-xk-1) 1≤k≤n
Метод наименьших квадратов
1. Формула метода наименьших квадратов, для линейной функции нескольких переменных.
2. Типовые способы преобразования нелинейной функции к линейной.
3. Метод наименьших квадратов для системы линейно – независимых функций.
4. Ряды и полиномы Фурье с использованием метода наименьших квадратов.
Пусть аппроксимируемая функция представляет собой функции n переменных y= f(x1…xn), которая задана таблицей своих значений:

информационная матрица
Такие таблицы формируются в ходе эксперимента для реальных объектов, у которых есть одна выходная переменная (отклик), которая зависит от нескольких выходных переменных (факторов).
SHAPE \* MERGEFORMAT

необходимо аппроксимировать нашу функцию при помощи построения линейной функции (приближающей).
Необходимо построить приближение данной функции f(x1…xn), заданной инфо - матрицей посредством функции φ (x1…xn)=y, которая должна быть линейной, т.е. ее общий вид:
y= φ (x1…xn)=b0+b1x1+…+bnxn (11.2)
bi – неизвестные коэффициенты (параметры)
Задача аппроксимации состоит в определении bi.
Каков критерий для выбора этих параметров?
Пусть f(x)-функция одной переменной и точки, в которой она определена, изображены на координатной плоскости.

Проводим прямую, минимизируем сумму квадратов расстояний.
Поскольку в ходе эксперимента на объект могут воздействовать случайные помехи, то в инфо – матрице могут присутствовать значения, которые не характерны для самой функции, в силу этого требовать от аппроксимирующей функции совпадения значений со значениями исходной функции во всех точках неверно.
Необходимо минимизировать сумму квадратов отклонений аппроксимирующей функции от исходных в заданных точках:
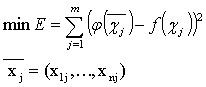
(11.3)
Для данной задачи критерий (11.3) будет иметь вид:
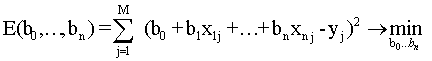
(11.4)
Функция квадратичная, параболоид. Точка, в которой производные частные все будут равны 0
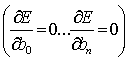
(11.5)
Так как функция (11.4) является квадратичной относительно переменных bi , то для нахождения ее минимума по этим переменным достаточно решить систему (11.5)

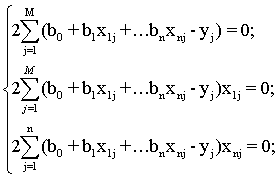
(11.6)
В системе (11.6) каждое уравнение делим на 2 и раскрываем сумму; перенося сумму с частью yj знак равенства:
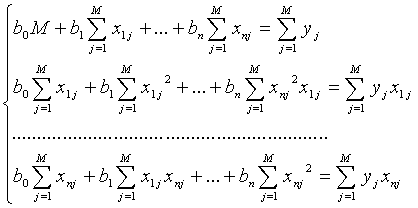
(11.7)
Система (11.7) представляет собой СЛАУ относительно bi и может быть решена одним из известных методов.
Для упрощения записи и решения представим систему (11.7) в матричном виде. Введем матрицы:
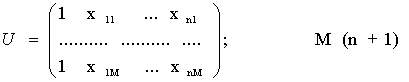
Столбец из 1 добавили в U с целью универсализации решений, так как линейную функцию можно представить в виде:
y= b0x0+b1x1+…+ bnxn, где x0=1
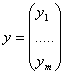
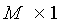
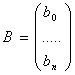
(n+1) 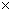
1
Тогда система (11.7) может быть записана в следующем виде:
[UTU]B=UTY (11.8)
Системы (11.7) и (11.8) называются нормальными. Используя, метод обратной матрицы система (11.8) имеет вид:
B= [UTU]-1UTY (11.9)
(11.9) - метод наименьших квадратов для линейной функции.
МНОГОЧЛЕНЫ ЧЕБЫШЕВА
1. Определение и свойства
2. Интерполяция по Чебышевским узлам
3. Многочлены равномерных приближений
4. Экономизация степенных рядов
Многочленом Чебышева n-ой степени называется функция
Tn(x)=cos (narccos) n=0,1,2 …,xÎ[-1;1] ; (9.1)
Докажем, что при любом n=0,1,2
n=0: T0(x)=cos0=1;
n=1: T1(x)=cos(arccos x)=x;
n=2: T2(x) =cos(2arccos x);
Обозначим α=arccosx
Tn(x)=cos2α ;
Tn+1(x)=cos((n+1)α) ;
Tn-1(x)=cos((n-1)α) ;
cos((n+1)α)+ cos((n-1)α)-2cos(2nα/ α)cos(2α/ α)=2 cosnα cosα;
Tn+1(x)+ Tn-1(x)=2 T1(x) Tn(x);
Tn+1(x)= 2xTn(x)- Tn-1(x); (9.2)
Свойства многочлена Чебышева:
1. Все функции Tn(x) являются многочленами при n=0,1,2,…
2. Степени этих многочленов возрастают с увеличением n, причем старший член Tn(x)=2n-1xn
3. Многочлены Tn(x) при четных n выражаются через четные функции , при нечетных n-через нечетные функции.
Проверим:
T2(x) =2х2-1
T3(x) =2х (2х2-1) =4х3-2х
T4(x) = 2х (4х3-3х)-2х2+1=23х4-3х2+1
4. На отрезке [-1;1] многочлен Tn(x) имеет ровно n различных действительных корней, которые рассчитываются по формуле:
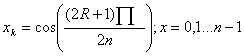
Докажем:
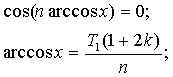
Так как arccosxÎ[0; Π];k=0,1,…n-1,чтобы туда попадал arcos
5. Корни многочлена Чебышева перемножаются, чередуются с точками их экстремума, причем максимум
Tn(x) на [-1;1] равен 1,т.е
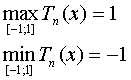
Для точек экстремума существует связь:
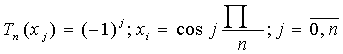
Введем нормированный многочлена Чебышева (старший коэффициент =1, перед х в максимальной степени)
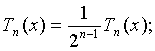
Теорема Чебышева
Из всех многочленов степени n со старшим коэффициентом = 1, нормированный многочлен Чебышева отклоняется от нуля на отрезке [-1;1] , т.е не существует многочлена Рn *(x), что :max | Рn*(x)| < max | T^n(x)|
[-1;1] [-1;1] Доказательство не нужно.
Интерполяция по Чебышевским узлам
Задача: Пусть есть некоторая функция f(x), определенная на отрезке [a;b]. Как расположить на отрезке [a;b] n+1 узел интерполяции таким образом, чтобы минимизировать максимальное отклонение интерполяционного полинома Лагранжа от f(x), т.е ошибку аппроксимации.Остаточный член полинома Лагранжа
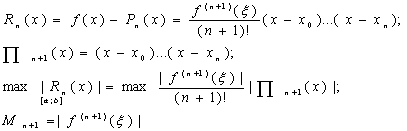
Необходимо минимизировать этот максимум, т.е необходимо найти такие узлы xk ,
Сведем [a;b] к отрезку [-1;1]
Должна существовать связь хÎ[a;b] с t Î[-1;1]
| a b |
| t |
| x |
| -1 1 |

Связь: x= Ct+D
C-коэффициент сжатия (растяжения, D-параллельный перенос)
Если t=1
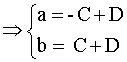
Если t=-1
Тогда:
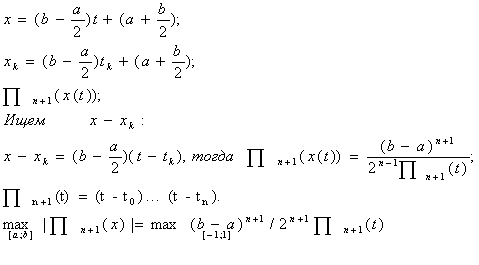
tkÎ[-1;1],
По теореме Чебышева полином Тn+1нормирован многочленом Чебышева, наименее отклонен от нуля на [-1;1], поэтому в качестве искомых корней необходимо взять корни многочлена Чебышева на [-1;1]
Узлы интерполяции, определим по формуле (9.5) обеспечивают min, max ошибку аппроксимации при помощи интерполяционных полиномов.
Многочлены равномерных приближений
Если функция f(x) ∞-но дифференцируема на [a;b] и в качестве узлов интерполяции берутся корни многочленов Чебышева, приведенные к [a;b], то справедливо:Т.е имеет место равномерная сходимость последовательности интерполяционного полинома Лагранжа функции f(x).
Теорема Вейерштрасса: для любой непрерывной функции f(x) на [a;b] найдется полином Qn(x), что |f(x)- Рn(x)| < ξ для любой ξ>0 , любое хÎ[a;b].
Т.е для любой f(x) непрерывной на [a;b],может быть построена аппроксимирующий наилучший полином, который минимизирует максимальное отклонение между f(x) и Qn(x). Такие полиномы называют многочленами наилучших равномерных приближений.
К сожалению, общий вид таких полиномов и способы построения не известны.
Экономизация степенных рядов
Ряд Тейлора представляет собой локальную аппроксимацию для f(x) степенной функции вида xn можно заменить многочлен Чебышева и получить разложение по этим многочленам вместо степенного ряда:Такой процесс называется экономизацией степенного ряда.
Разложение по многочленам Чебышева имеет меньшую максимальную погрешность.
ЛЕКЦИЯ №10,11
ИНТЕРПОЛЯЦИОННЫЕ СПЛАЙНЫ
Когда интерполяционный отрезок [a;b] велик, нет, основания считать, функцию f(x) достаточно гладкой, на [a;b], то нельзя повышать точность аппроксимации за счет увеличения степени интерполяционного многочлена.
Связано это с тем, что у многочлена n-ой степени может быть n-1 точка экстремума. При n→∞ график многочлена начинает сильно колебаться
Такое явление называют феноменом Рунге.
Поэтому более перспективным является применение кусочно-полиномиальной аппроксимации, при которой аппроксимирующая функция составляется из отдельных многочленов (сплайнов). Каждый из которых (одинаковы и наибольшей степени) определен на своем участке отрезка [a;b].
Рассмотрим аппроксимацию кусочно-линейной функции (линейный сплайн).
Пусть f(x) задана таблично на [a;b], т. е определены некоторые узлы интерполяции a≤x0<x1<…<xn≤b
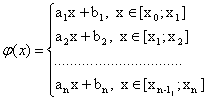
Необходимо: φ(xi)=yi=f(xi),
 Определим ai и bi.
Определим ai и bi. x=x0: φ(x0)=f(x0)=y0 a1x0+b1=y0
a2x1+b2=y1
x0 x1 x2
Получим систему:
а0x0+b1=y0 (решаем по отдельности каждую систему)
a2x1+b2=y1
a2x1+b2=y1
a2x2+b2=y2 (10.2)
anxn-1+bn=yn
anxn +bn= yn
Таким образом, получена система из 2n уравнений для поиска 2n неизвестных. Причем, система (10.2) образована из n систем линейных уравнений для 2-х неизвестных, каждая из которых может решаться независимо от остальных.

Кусочно-линейная функция φ(x) вида (10.1) внутри интервала (хi-1;xi),
Кусочно-квадратичная аппроксимация
Пусть f(x) задана таблично на [a;b], но n=2m (четно) a≤x0<x1<…<xn≤b
Чтобы функция приближала f(x) наложим ограничения φ(xi)=yi=f(xi),
Общее число узлов 2n+1, если n-четное.
Для нахождения неизвестных коэффициентов ak,bk,ck необходимо построить 3m условий.
k=1
[x0;x2]
Обобщим, получим систему:
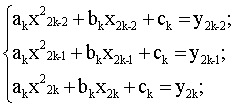
Для нахождения неизвестных имеем 3m условий. При каждом значении
Решать ее можем независимо от остальных условий.

Кусочно- квадратичная φ(x) вида (10.3) внутри интервала (x2n-2-x2n),
является непрерывной, но не дифференцируемой.
Определение Сплайна
Пусть на отрезке [a;b] задана некоторая система узлов a0≤x0< x1<…<xn ≤b
Сплайном Sn(x) называется функция, которая определена на [a;b], l раз непрерывна и дифференцируема на нем, при этом на каждом из отрезков
[хк-1; хк], к =
Разность (m-1) называется дефектом Сплайна (показывает разность между степенью составляющих его многочленов и степенью гладкости общей функции).
Если сплайн построен по некоторой таблично заданной функции f(x) таким образом, что S(хi)= f(xi); xi , i=
Очевидно, что функция (10.1) является интерполяционным сплайном степени 1, дефекта 1, а кусочно-квадратичная функция (10.3) является интерполяционным сплайном, степени 2, дефекта 2.
Интерполяционный сплайн степени 3, дефекта 1.
Дважды непрерывно – дифференцируемый – сплайн.
Пусть задана табличная функция на [a;b], причем a= χ0 ≤ χ1<…< χn=b (узлы сплайна совпадают с узлами интерполяции). Общий вид:
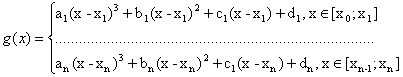
Условия:
1.) g(xi) = f(xi)=yi , i=
2.) g(x) = c2 (дважды дифференцируема) [a;b]
3.) – краевые условия
Для нахождения неизвестных коэффициентов введем функцию
gn(x) = ak(x-xk)3+ bk(x-xk)2+c1(x-xk)+dk, xÎ[ xk-1;xk]
1.) g1(x0) = y0 , g1(x1) = y1 , g2(x2) = y2 ,… gn(xn) = yn
2.) первое условие (сплайн интерполяционный)
3.)

Краевые условия:
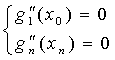
Таким образом, для нахождения 4n неизвестных мы построим 4n условий.
Теорема(10.1). Интерполяционный сплайн вида (10.5) для функции f(x) единственен.
Теорема(10.2). Пусть g(x)- интерполяционный сплайн степени 3 дефекта 1, построенный для функции f(x) С4 на отрезке [a;b], тогда для
|f(x)- g(x)|<C
Линейный фильтр
Понятие линейного сплайна позволяет сформулировать подходы к построению линейных фильтров, предназначенных для устранения случайных ошибок в данных.
Обычно в ходе измерений на процесс фиксации данных оказывают влияние случайные помехи. Для того, чтобы уменьшить влияние этих помех на качество интерполяции осуществляют пересчет значений функции в узлах интерполяции по следующей формуле:
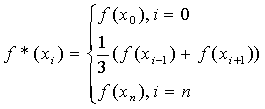
Квадратичный сплайн дефекта один
Узлы этого сплайна не совпадают с узлами интерполяции функции.
Пусть узлы интерполяции заданы на [a;b]
| χ0 χ1 χ2 χn-1 χn |
| |
| a |
| b |

Для сплайна n+2 узлов
Квадратичный сплайн дефекта 1 имеет вид:
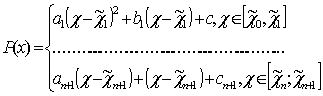
Условия:
1.)
2.) P(x) Î C'[a;b],
3.) Краевые условия:
P''(a)=A; P''(b)=B;
A и B- константы и желательно разные;
Чтобы построить сплайн необходимо найти 3n+3 неизвестных коэффициента. С этой целью сформирую функцию:
Pn(x)= ak
Условия:
1.) Pi+1=yi, i=
2.) Pk
P'k
3.) P1
Теорема 11.1. Квадр. Сплайн дефекта один, вида (11.1) для функции существует и единственен.
Теорема 11.2. Пусть функция f(x) дважды непрерывна и дифференцируема на [a;b], а P(x)- сплайн вида (11.1), тогда для
| f(x)-P(x) | ≤ C0∆2
| f '(x)-P' (x)|
| f ''(x)-P'' (x)|
где ∆- максимальное расстояние между узлами интерполяции, т.е ∆= max(xk-xk-1) 1≤k≤n
Метод наименьших квадратов
1. Формула метода наименьших квадратов, для линейной функции нескольких переменных.
2. Типовые способы преобразования нелинейной функции к линейной.
3. Метод наименьших квадратов для системы линейно – независимых функций.
4. Ряды и полиномы Фурье с использованием метода наименьших квадратов.
Пусть аппроксимируемая функция представляет собой функции n переменных y= f(x1…xn), которая задана таблицей своих значений:

информационная матрица
Такие таблицы формируются в ходе эксперимента для реальных объектов, у которых есть одна выходная переменная (отклик), которая зависит от нескольких выходных переменных (факторов).
SHAPE \* MERGEFORMAT
| xn |
| x1 |
| ……………… |
| y |

необходимо аппроксимировать нашу функцию при помощи построения линейной функции (приближающей).
Необходимо построить приближение данной функции f(x1…xn), заданной инфо - матрицей посредством функции φ (x1…xn)=y, которая должна быть линейной, т.е. ее общий вид:
y= φ (x1…xn)=b0+b1x1+…+bnxn (11.2)
bi – неизвестные коэффициенты (параметры)
Задача аппроксимации состоит в определении bi.
Каков критерий для выбора этих параметров?
Пусть f(x)-функция одной переменной и точки, в которой она определена, изображены на координатной плоскости.
| x1 x2 x3 x4 x5 x |
| y y5 y2 y4 y3 y1 |
| (x5;y5) |
| (x1;y1) |
| (x3;y3) |
| (x2;y2) |
| (x4;y4) |

Проводим прямую, минимизируем сумму квадратов расстояний.
Поскольку в ходе эксперимента на объект могут воздействовать случайные помехи, то в инфо – матрице могут присутствовать значения, которые не характерны для самой функции, в силу этого требовать от аппроксимирующей функции совпадения значений со значениями исходной функции во всех точках неверно.
Необходимо минимизировать сумму квадратов отклонений аппроксимирующей функции от исходных в заданных точках:
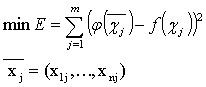
Для данной задачи критерий (11.3) будет иметь вид:
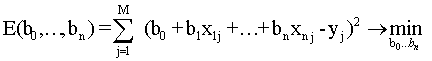
Функция квадратичная, параболоид. Точка, в которой производные частные все будут равны 0
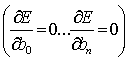
Так как функция (11.4) является квадратичной относительно переменных bi , то для нахождения ее минимума по этим переменным достаточно решить систему (11.5)
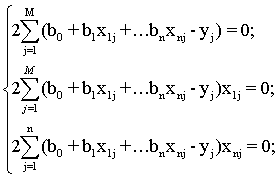
В системе (11.6) каждое уравнение делим на 2 и раскрываем сумму; перенося сумму с частью yj знак равенства:
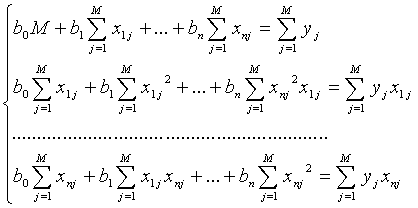
Система (11.7) представляет собой СЛАУ относительно bi и может быть решена одним из известных методов.
Для упрощения записи и решения представим систему (11.7) в матричном виде. Введем матрицы:
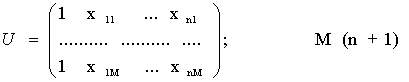
Столбец из 1 добавили в U с целью универсализации решений, так как линейную функцию можно представить в виде:
y= b0x0+b1x1+…+ bnxn, где x0=1
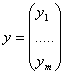
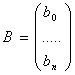
Тогда система (11.7) может быть записана в следующем виде:
[UTU]B=UTY (11.8)
Системы (11.7) и (11.8) называются нормальными. Используя, метод обратной матрицы система (11.8) имеет вид:
B= [UTU]-1UTY (11.9)
(11.9) - метод наименьших квадратов для линейной функции.