Иванов Георгий Петрович

Свободные токи, текущие в проводниках, расположенных в магнитном поле, и возбуждающие силы Ампера, уже давно и успешно (вместе со связанными токами) приводят в движение наземные и водные транспортные средства - электропоезда, электромобили, электроходы. Однако, пока еще мало кто знает об их скрытых резервах. Свободные токи способны приводить в движение космические корабли и держать "на весу" на любой высоте любые тяжести, причем, без какого либо загрязнения окружающей среды вещественным или энергетически мусором. На то свойство силы Ампера, благодаря которому подобное возможно, уже давно указал известный физик И. Е. Тамм, а, вслед за ним, другой известный физик Р. Фейнман.

Часть 1. И. Е. Тамм и Р. Фейнман о "количестве движения статического поля" и неизвестная форма материи

"Количество движения статического поля" это такой же камень преткновения для современной физики каким были опыт Майкельсона и "ультрафиолетовая катастрофа" для физики прошлого. Это свидетельство не менее глубокого кризиса физической науки, который постиг ее сто лет назад. Оказывается, что требование выполнения закона сохранения количества движения связано с существованием несводимой к веществу и полю формы материи.

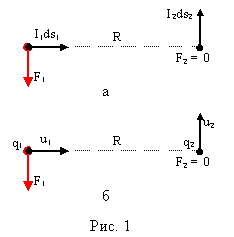
В известном всем студентам-физикам курсе классической электродинамики "Основы теории электричества" [1], впервые изданном еще в 1929 и многократно, вплоть до последнего времени, переиздававшемся И. Е. Тамм рассматривает следующую ситуацию (см. Рис. 1а).

Элемент тока I1ds1 находится на расстоянии R от перпендикулярного к нему по направлению элементу тока I2ds2. При этом на элемент тока I1ds1, под влиянием магнитного поля, образуемого элементом тока I2ds2 будет действовать сила F1. Так как магнитное поле, образуемое элементом тока I1ds1 на линии этого тока равно нулю, то равна нулю и сила F2, действующая на элемент тока I2ds2. Выходит, суммарная сила (равнодействующая рассматриваемой системы двух токов) равна F1, т. е. отличается от нуля.

Описываемая ситуация совершенно аналогична, той, которую рассматривает Р. Фейнман в [2] (см. Рис. 1б). Разница лишь в том, что роль элементов тока выполняют не участки контуров, по которым течет ток (т. е. движутся по проводнику заряды), а движущиеся в пространстве свободные заряды q1 и q2. Элементы контуров и движущиеся заряды ничем не отличаются друг от друга в отношении создания ими магнитных полей и, испытываемых в магнитном поле сил (Ids = qu). Точно так же отличается от нуля и равнодействующая системы двух движущихся зарядов, что очевидно при сравнении Рис. 1а и Рис. 1б. Отметим, что на заряды q1, q2 будут также действовать не дающие вклад в равнодействующую и, поэтому не показанные на чертеже, равные по величине, противоположные по направлению кулоновские силы.

Что же получается? Неужели, нарушение принципа равенства действия и противодействия? Однако каждый, имеющий какое то представление о фундаментальных основах физики, верит (включая автора настоящей статьи), что закон сохранения количества движения выполняется при всех обстоятельствах. Следовательно есть какие-то неучтенные факторы. Что по этому поводу говорят классики, на которых мы ссылаемся.

И. Е. Тамм пишет: - "… в случае постоянных токов, по необходимости являющихся замкнутыми, это нарушение третьей аксиомы Ньютона связано лишь с представлением сил взаимодействия токов как сил попарного взаимодействия их элементов. Действительно, силы взаимодействия двух замкнутых токов удовлетворяют принципу равенства действия и противодействия". Но Тамм, мягко говоря, оставил без рассмотрения тот факт, что элементы токов - это, в общем случае, не просто какие то части замкнутых контуров, которые, по его мнению, не стоит рассматривать вне связи с этими контурами - это самостоятельные реальные сущности, которые можно представлять себе в виде движущихся заряженных частиц, что и делает Р. Фейнман. Таким образом, замкнутые контуры, за которыми спрятался Тамм, есть ни что иное как декорация, скрывающая суть дела от читателей его курса электродинамики (в других отношениях, замечательного).

Р. Фейнман демонстрирует другой подход к решению проблемы. Он пишет [2, стр303]: - "Силы, действующие на эти частицы, не уравновешивают друг друга, так что действие и противодействие оказываются неравными, а полный импульс вещества должен изменяться. Он не сохраняется. Но в такой ситуации изменяется и импульс поля. Если Вы рассмотрите величину импульса, задаваемого вектором Пойнтинга, то она оказывается непостоянной. Однако, изменение импульса частицы в точности компенсируется импульсом поля, так что полный импульс частиц и поля все же сохраняется.".

Следует обратить особое внимание на то, что речь идет вовсе не о том импульсе и векторе Пойнтинга, который переносят электромагнитные волны (волновые электромагнитные поля). В самом деле, предполагается, что частицы, изображенные на Рис. 1б, движутся равномерно и прямолинейно, так что ни о каком излучении электромагнитный волн не может быть и речи. То же самое относится и к элементам тока, изображенным на Рис. 1а, т. к. постоянные токи тоже ничего не излучают. Речь идет об импульсе неволновых, независимых друг от друга электрического и магнитного полей, который в научной литературе известен под названиями "скрытый импульс", "потенциальный импульс", "статический импульс". И. Е. Тамм в своей книге [1, с. 404, 405] употребляет название "количество движения статического поля" и пишет, что "… общее количество движения статического поля в целом по необходимости равно нулю". Это его мнение вошло даже в известную пятитомную "Физическую энциклопедию" под ред. А. М. Прохорова.

Таким образом, И. Е. Тамм категорически отвергает ту причину "нарушения принципа равенства действия и противодействия", которую Р. Фейнман считает истиной в последней инстанции. Вот Вам и "драма идей", свидетельствующая о подлинной неординарности простейшей, на первой взгляд, задачи о взаимодействии элементов тока. Других вариантов решения, кроме предложенного Р. Фейнманом, во всей ортодоксальной науке сегодняшнего дня не существует. Разве этот факт сам по себе не заслуживает самого пристального внимания научной общественности и отдельных ученых?

Может быть, Фейнман все-таки прав? Что ж тогда не нравится Тамму? Может быть то, что центр инерции системы двух заряженных частиц, изображенных на Рис. 1б, под действием результирующей силы F1, стал бы смещаться, в направлении этой силы, ведь электрические и магнитные статические поля при малых скоростях частиц будут следовать вместе с ними, как привязанные. О каком тогда законе сохранения импульса можно говорить?

Есть и другая, более веская, причина не верить Фейнману. Допустим, его концепция верна. Тогда частицы и создаваемые ими поля образуют замкнутую систему, количество движения (импульс) и энергия которой сохраняются. Отсюда следует:

dp + dG = 0

где p - импульс вещества (частиц), G - импульс поля. Применительно к ситуации, изображенной на Рис. 1б можно записать: p = p1 + p2, где p1, p2 - импульсы частиц с зарядами q1, q2, соответственно. Подставляя p1 = m1v1 (m1, v1 - масса и скорость первой частицы) и, учитывая, что dp2 = 0, получим:

dp1 = - dG (1)

Из закона сохранения энергии следует, что:

p12/2m1 + p22/2m2 + U= 0 (2)

где U - энергия поля. Дифференцируя (2) и, учитывая, что соотношение между импульсом и энергией статического и волнового полей одно и то же (см. [2, с. 302]), U = c G (с - скорость света), получим:

v1dp1 = -cdG (3)

Сопоставляя (1) и (3), видим что концепция "количества движения статического поля" не согласуется с законом сохранения энергии т. к. уравнение (3), выражающее закон сохранения энергии не имеет решений для скоростей частиц, меньших скорости света. Совершенно идентичный вывод в наглядной и убедительной форме получен в результате анализа классического опыта Грехема и Лахоза [3] на примере системы другого рода (см. статью ). Таким образом, И. Е. Тамм прав. Его приведенное выше утверждение о нулевом импульсе статического поля оправдывается.

Выходит, Р. Фейнман ошибается. Однако, вычисление величины, которую он называет импульсом поля G системы двух движущихся зарядов (Рис. 1б) путем интегрирования плотности импульса g = [EH]/c2 (E и H - напряженности электрического и магнитного полей) по всему бесконечному пространству дает ненулевой результат. Мало того, изменение этой величины, имеющей размерность импульса, соответствует изменению количества движения частиц под действием силы Лоренца, так, что формула (1) формально выполняется. Тогда, может быть, несмотря на отсутствие согласования с законом сохранения энергии, величина G все-таки, является импульсом поля, изменение которого компенсирует силу, действующую на частицу и прав не Тамм, а Фейнман?

Согласно исследованиям, приведенным в [4] и на сайте (раздел "Академический вариант", "Аспекты" - статья "Таково мнение магнитодинамической силы"), а также в одноименной статье , величина G не является импульсом, т. к. сохраняется только при неизменных скоростях частиц. К примеру, ускорение одной из частиц (пусть даже, настолько слабое, что эффекты излучения электромагнитных волн не играют никакой роли), изображенных на Рис. 1б приведет к изменению магнитного поля и, как следствие, величины G, хотя механический импульс системы останется прежним. Таким образом, при изменении скорости G не сохраняется, следовательно, эта величина не может быть импульсом, который сохраняется всегда. В то же время, при постоянстве скоростей, изменение величины G, названной импульсным потенциалом, является мерой изменения механического импульса частиц системы.

Подведем итог. Сила Лоренца (Ампера), возникающая при взаимодействии движущихся зарядов (элементов тока) не встречает противодействия со стороны других движущихся зарядов (со стороны вещества). Таково ее неотъемлемое природное свойство. Попытка Р Фейнмана включить в систему "количество движения статического поля" не выдерживает критики, т. к такое "количество движения" , во-первых не сохраняется, во-вторых, не согласуется с законом сохранения энергии. Выходит, что сила Лоренца (Ампера) не находит противодействия со стороны всех известных современной науке форм материи - вещества и поля. Иными словами, полный импульс вещества и поля не сохраняется. Отсюда вывод: закон сохранения количества движения явно и ясно указывает на существование неизвестной современной науке формы материи, отличающейся как от вещества, так и от поля. Эта материя заполняет все физическое пространство. Она вступает в силовое (импульсное) взаимодействие с веществом, создавая противодействие известным силам Лоренца и Ампера. Противодействующая сила лежит на той же линии действия, что и сила Лоренца (Ампера), равна ей по величине и противоположна по направлению. Так просто и естественно решается проблема неравенства действия и противодействия при взаимодействии движущихся зарядов (элементов тока). Полученный вывод не гипотеза автора. К нему неотвратимо ведут традиционные задачи классической электродинамики, решаемые традиционными методами. Неизвестная форма материи, получившая название "электровакуум" (см. [4] или сайт), является неотъемлемой структурной частью более общего вида материи физического вакуума или, как говорили ранее - эфира. Остается добавить, что слишком ретивые и недальновидные последователи А. Эйнштейна - релятивисты -явно поспешили изгнать из науки понятие "эфир", вопреки мнению своего наставника. Иначе подобные выводы уже давно были бы сделаны и внедрены в практику. Сам Эйнштейн писал, что физика без эфира немыслима, что без него невозможно представить себе распространение света, силовое взаимодействие на расстоянии и т. д. (см. в изданном на русском языке сборнике его трудов статью "Эфир и теория относительности"). Теория относительности, в понимании Эйнштейна, налагает запрет не на существование эфира, а на возможность наблюдения за перемещением, по отношению к нему. Таким образом, в противовес прозорливому Эйнштейну, его последователи - релятивисты - явно страдают научной слепотой. Слепцы изгнали эфир из науки - вернуть его, дело зрячих. Отрицание эфира эквивалентно отрицанию закона сохранения количества движения.

Часть 2. Непознанные возможности силы Ампера

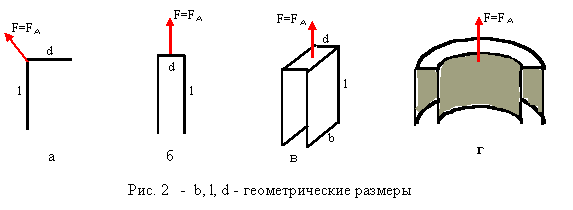
Представляет интерес рассмотреть результирующие силы, возникающие в проводящих переменные токи (металлических или неметаллических) структурах, изображенных на Рис. 2а,б,в.г.

Это могут быть линейные (Рис. 2а,б) или объемные (Рис. 2в,г) вибраторы (если длина волны, соответствующая частоте возбуждаемых токов, намного превосходит их геометрические размеры) или же резонаторы (геометрические размеры соответствуют условиям возбуждения резонансных частот). Наше рассмотрение касающееся, в основном, вибраторов (квазистационарное приближение), в определенной степени приложимо и к резонаторам, максимальные размеры которых не превосходят четверти длины волны, так что условие малости геометрических размеров, в грубом приближении, все-таки выполнятся. Характер сил для вибраторов и резонаторов фактически один и тот же, просто, формулы, полученные для вибраторов, не годятся для точных расчетов применительно к резонаторам, но ими можно пользоваться как оценочными. Важная характерная особенность рассматриваемых структур состоит в том, что токи проводимости текут в них по разомкнутым контурам, возбуждая в окружающем пространстве максвелловские токи смещения. В квазистационарном случае, будет равной нулю сумма токов смещения и проводимости, пересекающих поверхность, ограниченную замкнутым контуром, размеры которого намного превосходят геометрические размеры вибраторов.

Изображенные на Рис. 2а,б,в,г объекты можно представить себе как совокупность взаимодействующих пар зарядов, осциллирующих с малой (по сравнению с геометрическими размерами) амплитудой. Рассмотрим подробнее одну из таких пар.

Пусть заряды q1, q2 совершают синфазные колебательные движения малой (по сравнению с R) амплитуды по гармоническому закону относительно неподвижных массивных противоположно заряженных центров см. Рис. 3. Размеры системы предполагаются малыми, по сравнению по сравнению с длиной волны, соответствующей

частоте колебаний зарядов. Не снижая общности, можно ограничиться случаем, когда скорости зарядов взаимно перпендикулярны (параллельные компоненты образуют равные по величине и противоположные по направлению силы Лоренца, в силу чего, как увидим ниже, дают нулевой вклад в равнодействующую). В какой-то момент времени скорости зарядов u1, u2, малые, по сравнению со скоростью света, будут иметь направления, как указано на рисунке. Каждый из движущихся зарядов будет возбуждать в окружающем пространстве магнитное поле, индукцию B которого в точке нахождения другого заряда можно определить по формуле:

где R - расстояние между зарядами. На каждый из зарядов со стороны магнитного поля, создаваемого другим зарядом будет действовать сила Лоренца FL1, FL2, так что суммарная сила Лоренца в системе FL = FL1 + FL2. Отсюда после подстановок и алгебраических преобразование получим:

 (4)

Так как, по условию задачи, заряды q1, q2 колеблются по гармоническому закону, то они совершают ускорения w1, w2, индуцируя электрические поля. При этом на заряд q2 (q1) со стороны поля индукции, образуемого зарядом q1 (q2) будет действовать сила F2i (F1i):

 (5)

В свою очередь, заряд q1 (q2) будет испытывать влияние, так называемой, магнитодинамической силы F1m (F2m) со стороны поля заряда q2 (q1). Эта, известная из классической электродинамики, но редко встречающаяся на страницах научной литературы, сила появляется при изменении намагниченности вещества в присутствии электрического поля [5],[6]. Применительно к ускоренно движущимся зарядам, она подробно рассмотрена на сайте [http://www.tts.lt/~nara] (раздел "Академический вариант", "Аспекты" - статья "Таково мнение магнитодинамической силы"), а также в одноименной статье . Эта сила равна по величине и противоположна по направлению, возбуждаемой ею силе индукции:

 (6)

Следовательно, все силы индукции компенсируются силами магнитодинамическими и, по этой причине, не дают никакого вклада в равнодействующую системы (поэтому, как и кулоновские силы, не показаны на чертеже).

Заметим, что рассмотренное выше индукционное электрическое поле Ei, в другом аспекте, есть нечто иное, как электрическая компонента дипольного электромагнитного излучения, возбуждаемого ускоренно движущимся зарядом. Ему соответствует магнитная компонента Hi, влияние которой тоже следует учитывать, т. к она будет вносить свой вклад в испытываемую частицами силу Лоренца. Найдем отношение величины силы Лоренца Fw, возбуждаемой магнитной компонентой волнового излучения Hw, зависящей от ускорения w заряда, к силе Лоренца Fu, возбуждаемой магнитным полем Hu, определяемым его скоростью u. Получим:

Fw/ Fu = Hw/ Hu = 2p R/l = kR

где l - длина волны, k - волновое число. Отсюда заключаем, что принятое нами условие, малости размеров системы, по сравнению с длиной волны, позволяет не учитывать влияние магнитной компоненты волнового излучения.

Получается так, что равнодействующую F рассматриваемой системы двух зарядов определяют одни только силы Лоренца:

F = FL (7)

Все остальные участвующие во взаимодействии зарядов силы либо взаимно уничтожаются, либо пренебрежимо малы.

Так как, по условию задачи, скорости изменяются синфазно по гармоническому закону, то полагая, u1 = u1mcosw t, u2 = u2mcosw t (u1m, u2m - амплитуды скоростей частиц ), и, пользуясь (4), можно найти усредненную по времени равнодействующую системы Fср:

 (8)

где n1, n2 - единичные векторы вдоль принятых за положительные направлений скоростей зарядов, nR- единичный вектор вдоль направления радиус-вектора расстояния между зарядами.

Формула (8) показывает, что равнодействующая системы двух движущихся зарядов, представляющая собой суммарную силу Лоренца, отлична от нуля и имеет постоянное направление.

Следует отметить, что ограничение Rl равнодействующая все также равна суммарной силе Лоренца, хотя последняя определяется уже не скоростью, а ускорением зарядов. Из-за явления запаздывания будут взаимно уничтожаться не мгновенные, а средние значения индукционных и магнитодинамических сил, что не отразится на равнодействующей системы.

Возвращаясь к вибраторам, видим, что действующие на них силы могут быть найдены как результат интегрирования по парам рассмотренных нами осциллирующих зарядов. После интегрирования силы взаимодействия между движущимися зарядами будут сведены к взаимодействию токов. Отсюда, равнодействующая для систем, изображенных на Рис. 2 есть не что иное как результирующая сила Ампера, действующая на участки проводников с токами, текущими в магнитных полях, создаваемым другими участками проводников с токами.

Вычисления дают следующие результаты для амплитудного значения равнодействующей F вибраторов, по которым течет ток I.

Г-образный контур (Рис. 2а), согнутый из проволоки, радиусом r, при условии