Введение в теорию многоэлектронного атома

Водородоподобные орбитали

1. Атом H и водородоподобный ион. Возмущение потенциала и расщепление уровней АО. Правило Маделунга-Клечковского.
АО водородоподобных ионов - это волновые функции возможных состояний единственного электрона в электростатическом поле. Потенциальная энергия кулоновского притяжения единственного электрона к ядру в систем СГС выражается функцией вида . График этой функции – гипербола. Именно этот потенциал ответственен за очень высокую кратность вырождения уровней АО.
Наш знаменитый физик-теоретик академик Владимир Александрович Фок показал, что симметрия атома H (и одноэлектронного водородоподобного иона) существенно выше, чем симметрия простой трёхмерной сферы, и назвал её симметрией "четырёхмерного шара".
Очень общее свойство квантово-механических систем таково, что, кратность вырождения энергетических уровней тем выше, чем выше симметрия системы, и, напротив, любое возмущение системы искажает её симметрию, вызывая расщепление вырожденных уровней.
Этот эффект исследуют с помощью модельных приёмов теории. Так понижение симметрии одноэлектронного водородоподобного иона можно искусственно смоделировать, искажая вид потенциала. Такой приём приводится в книге знаменитого Э. Ферми (см. "Конспект лекций по квантовой механике"). Искусственно искажая потенциал, прослеживают, как это влияет на уровни АО. Для этого в модельный потенциал вводится дополнительный параметр :
. (1)
При ®0 получается предельное выражение вида , но искомое искажение центрального кулоновского потенциала достигается при ¹ 0.
Последствия такого искажения потенциала хорошо знакомы даже начинающему химику.
Уровни АО в водородоподобном ионе зависят только от главного квантового числа n и характеризуются очень высокой кратностью вырождения. Иными словами энергия всех состояний с разными l но с одним и тем же n одна и та же, т.е. все АО принадлежат одному и тому же уровню. При возмущении потенциала такой уровень расщепляется, и из него возникают несколько новых уровней, которые зависят уже не только от общего главного, но и от побочного квантового числа.
Их часто ещё называют подуровнями, как бы подчёркивая, что у них общее главное квантовое число, и все они остаются внутри некоторого сравнительно узкого интервала значений.
Расщеплённые уровни АО многоэлектронного атома подчиняются правилу Клечковского-Маделунга: "Уровни АО многоэлектронного атома возрастают с увеличением суммы двух квантовых чисел n+l, а при равных значениях суммы n+l глубже лежит уровень с меньшим значением n (т.е. большим l)".
Последовательность энергетических уровней АО многоэлектронного атома подчиняется правилу Клечковского-Маделунга.

n+l	N,l	АО	n+l	n,l	АО	n+l	n,l	АО	n+l	n,l	АО	n+l	n,l	АО	n+l	n,l	АO
1	1,0	1s	3	2,1	2p	5	3,2	3d	6	4,2	4d	7	4,3	4f	8	5,3	5f
2	2,0	2s		3,0	3s		4,1	4p		5,1	5p		5,2	5d		6,2	6d
			4	3,1	3p		5,0	5s		6,0	6s		6,1	6p		7,1	7p
				4,0	4s								7,0	7s		8,0	8s

Этот результат удобно проиллюстрировать, сравнивая две энергетические диаграммы АО:
Таблица и график справа воспроизводят последовательность уровней АО многоэлектронного атома:
1s<2s<2p<3s<3p<4s<3d<4p<5s<4d<5p<6s<4f<5d<6p<7s<5f<6d<7p<8s
9.2. Водородоподобные орбитали. Многоэлектронный гамильтониан атомной оболочки. Межэлектронное отталкивание как экранирование ядра. Одноэлектронное приближение. Орбитали многоэлектронного атома.

2. Элементы теории многоэлектронных атомов

2.1. Многоэлектронный атом. Содержание. Электронный гамильтониан многоэлектронного атома. Отталкивание электронов, потенциальная энергия отталкивания и ее приближенное представление в виде функции экранирования ядра. Эффективный заряд ядра. Орбитали Слейтера. Одноэлектронный приближение в теории многоэлектронного атома. Атомные орбитали многоэлектронных атомов, уровни и последовательность заполнения. Правило Клечковского-Маделунга. Модификация формулы Бора. Спин электрона.
Одноэлектронное приближение.
Полная энергия электронной оболочки многоэлектронного атома состоит из нескольких слагаемых, и отображающий её многоэлектронный гамильтониан атома также включает в себя несколько слагаемых. Это следующие операторы:
Оператор кинетической энергии каждого электрона, равный
T= - (1/2) Ñ2,()
Оператор потенциальной энергии притяжения к ядру каждого электрона, равный
U(ri) = - Ze2/r,()
Оператор потенциальной энергии притяжения каждого электрона к ядру, равный
Оператор потенциальной энергии отталкивания электрона от прочих электронов, равныйU(rij) = S-Ze2/rij,()
Оператор потенциальной энергии отталкивания электрона от прочих электронов, равныйU(rij) = S-Ze2/rij,()
Принципы заполнения атомно-орбитальных уровней и построение основных электронных конфигураций: 1) водородоподобие (одноэлектронное приближение в атоме), 2) минимум энергии, 3) принцип Паули, 4) максимальный суммарный спин (1-е правило Хунда). Примеры основных электронных конфигураций легких атомов. Возбужденные атомные конфигурации.
Схема приближенного представления энергии электронного отталкивания в виде энергии экранирования ядра.
Все двухэлектронные слагаемые отталкивания в гамильтониане оболочки атома образуют двумерный косоугольный массив. Их следует просуммировать и приближённо представить суммой, слагаемые которой распределены по отдельным частицам. В таком приближении многоэлектронный гамильтониан примет аддитивный вид. На этом основании можно ввести приближение независимых электронов-"одноэлектронное" приближение.

Номера и координаты частиц		1	2	3	4		i		j		z
	V1		V12	V13	V14	...	V1i		V1j		V1z
	V2			V23	V24	...	...		...		V2z
...	...		...	...	...	...	...		...		...
	Vi		...	...	...	...	...		Vij		Viz
...	...		...	...	...	...	...		...		...
	Vj						Vji		...		Vjz
...	...		...				...		...		...
	Vz-1								...		Vz-1,z
	Vz		...	...	...	...	...		...

Отдельные диагональные слагаемые этой таблицы равны Vi= –Ze2/ri. Каждое из них представляет из себя энергию электростатического кулоновского притяжения одного из электронов к ядру. Недиагональные слагаемые Vij=+Ze2/rij. Полное выражение электростатической потенциальной энегии в атоме:  Результирующий эффективный потенциал межэлектронного отталкивания превращается в эффективный потенциал "экранирования" ядра:

s(ri) - заряд экранирования (функция экранирования) отдельного электрона  внутренними электронами, более близкими к ядру.
В этом случае потенциальная кулоновская энергия притяжения всех электронов к ядру дополняется эффективной потенциальной функцией экранирования ядра, и получается эффективное приближённое аддитивное выражение для всей кулоновской потенциальной энергии электронной оболочки

Микросостояния и атомные термы в приближении Рассела-Саундерса.
Этот раздел целесообразно рассмотреть на конкретных примерах.
Содержание. Электронная конфигурация. Микросостояния и их систематизация. Порядок учёта кулоновских взаимодействий и постадийная классификация дискретных электронных уровней и состояний атома (электронно-ядерное притяжение и орбитальные уровни, межэлектронное отталкивание и атомные термы Рассел-Саундерса, спин-спиновая корреляция и запрет Паули). Суммарные квантовые числа ML,MS,L,S. Атомное внутреннее квантовое число J. Термы нормальные и обращённые. Правила Хунда (1-е, 2-е и 3-е). Относительная шкала энергии атомных термов. Спектральные переходы и правила отбора. Атомные уровни в магнитном поле, эффект Зеемана (практикум).
Электронная конфигурация представляет собой исходное понятие. Оно определяется в нулевом приближении в оценке энергии. Далее постепенно учитываются всё более тонкие взаимодействия, и возникает более точная картина состояний и уровней многоэлектронного атома. Если атомный подуровень заселён неполностью, то возникает несколько различных микросостояний. Их характеристики непосредственно определяются комбинаторикой размещений электронов в системе спин-орбиталей.
Если n электронов заселяют g спин-орбиталей, то одно из формальных обозначений конфигурации (g,n). В её пределах число возможных микросостояний определяется согласно статистике Ферми: W(g,n) = g! / [n! (g - n) !].
Пример 1: основная электронная конфигурация атома углерода C (1s22s22p2)
Конфигурация p2 (атомы IV группы элементов C, Si. .). W(6,2) = 6! / [2! (6 - 2) !] =15

Перечислим все возможные варианты орбитальных размещений и спиновых комбина-ций 2-х электронов на трёх АО:

Орбитальные распределения двух электронов

Возможно всего шесть размещений внутри p-АО без учёта спина Орбитальные распре-деления можно охарак-теризовать комбинаци-ями квантовых чисел частиц (m1, m2): (+1,+1) А (0, 0) Б (- 1, - 1) В (+1, 0) Г (+1, - 1) Д (0, - 1) Е

Комбинации пространственных (орбитальных) состояний частиц в коллективе легко описать разными способами. Возможные спиновые комбинации в системе двух частиц-фермионов с половинным спином (электронов, протонов,. .) можно представить разными способами. Можно изобразить ориентации спинов разными символами (стрелками, знаками или греческими буквами). Результат сложения компонент момента импульса вдоль оси вращения представми в одной из строк таблицы значениями суммарного магнитногоквантового числа. Все возможные комбинации спиновых векторво отдельных электронов попадут в таблицу:

Способ 1	SYMBOL 173 \f "Symbol" \s 12­SYMBOL 173 \f "Symbol" \s 12­	SYMBOL 173 \f "Symbol" \s 12­SYMBOL 175 \f "Symbol" \s 12Ї	SYMBOL 175 \f "Symbol" \s 12ЇSYMBOL 173 \f "Symbol" \s 12­	SYMBOL 175 \f "Symbol" \s 12ЇSYMBOL 175 \f "Symbol" \s 12Ї	Эти три способа
Способ 2	(++)	(– +)	(–+)	(– –)	Описания
Способ 3	SYMBOL 97 \f "Symbol" \s 12aSYMBOL 97 \f "Symbol" \s 12a	SYMBOL 97 \f "Symbol" \s 12aSYMBOL 98 \f "Symbol" \s 12b	SYMBOL 98 \f "Symbol" \s 12bSYMBOL 97 \f "Symbol" \s 12a	SYMBOL 98 \f "Symbol" \s 12bSYMBOL 98 \f "Symbol" \s 12b	Идентичны
	Можно как-либо еще, а в итоге будет:				где MS(1,2) = mS(1) + mS(2)
MS(1,2)	1	0	0	-1

MS(1,2)	+1	0		–1
Микросостояния в рамке, выделенные на тёмном фоне, принципу Паули не удовлетворяют и должны быть исключены из дальнейшего анализа	A SYMBOL 97 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12	АSYMBOL 97 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12 SYMBOL 186 \f "Symbol" \s 12 АSYMBOL 98 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12		АSYMBOL 98 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12
	A SYMBOL 97 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12	БSYMBOL 97 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12 SYMBOL 186 \f "Symbol" \s 12 БSYMBOL 98 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12		A SYMBOL 98 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12
	A SYMBOL 97 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12	ВSYMBOL 97 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12 SYMBOL 186 \f "Symbol" \s 12 ВSYMBOL 98 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12		A SYMBOL 98 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12
	ГSYMBOL 97 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12	ГSYMBOL 97 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12	ГSYMBOL 98 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12	ГSYMBOL 98 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12
	ДSYMBOL 97 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12	ДSYMBOL 97 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12	ДSYMBOL 98 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12	ДSYMBOL 98 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12
	ЕSYMBOL 97 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12	ЕSYMBOL 97 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12	ЕSYMBOL 98 \f "Symbol" \s 12SYMBOL 97 \f "Symbol" \s 12	ЕSYMBOL 98 \f "Symbol" \s 12SYMBOL 98 \f "Symbol" \s 12

Из сочетания одного из орбитальных и одного из спиновых распределений с учётом запрета Паули (на одной и той же орбитали запрещены комбинации с параллельными спинами SYMBOL 97 \f "Symbol" \s 12aSYMBOL 97 \f "Symbol" \s 12a и SYMBOL 98 \f "Symbol" \s 12bSYMBOL 98 \f "Symbol" \s 12b) получается одна из возможных спин-орбитальных комбинаций. Такую комбинацию (размещение) называют микросостоянием оболочки. Микросостояния, выделенные жирным шрифтом в каждой отдельной ячейке таблицы, физически тождественны (SYMBOL 186 \f "Symbol" \s 12). Нет способов различить состояния отдельных частиц в пределах общей орбитали - фазовой ячейки. Всего получено 15 микросостояний электронной оболочки в исследуемой конфигу-рации. Сравним разные приёмы табулирования признаков микросостояний.

Например:

1 0 -1 ML= ml(1)+ml(2) MS= ml(1)+ml(2) SYMBOL 173 \f "Symbol" \s 12­SYMBOL 175 \f "Symbol" \s 12¯ АSYMBOL 97 \f "Symbol" \s 12aSYMBOL 98 \f "Symbol" \s 12b 2 0 SYMBOL 173 \f "Symbol" \s 12­SYMBOL 175 \f "Symbol" \s 12¯ БSYMBOL 97 \f "Symbol" \s 12aSYMBOL 98 \f "Symbol" \s 12b 0 0 SYMBOL 173 \f "Symbol" \s 12­SYMBOL 175 \f "Symbol" \s 12¯ ВSYMBOL 97 \f "Symbol" \s 12aSYMBOL 98 \f "Symbol" \s 12b -2 0 SYMBOL 173 \f "Symbol" \s 12­ SYMBOL 173 \f "Symbol" \s 12­ ГSYMBOL 97 \f "Symbol" \s 12aSYMBOL 97 \f "Symbol" \s 12a 1 1 SYMBOL 173 \f "Symbol" \s 12­ SYMBOL 175 \f "Symbol" \s 12¯ ГSYMBOL 97 \f "Symbol" \s 12aSYMBOL 98 \f "Symbol" \s 12b 1 0 SYMBOL 175 \f "Symbol" \s 12¯ SYMBOL 173 \f "Symbol" \s 12­ ГSYMBOL 98 \f "Symbol" \s 12bSYMBOL 97 \f "Symbol" \s 12a 1 0 SYMBOL 175 \f "Symbol" \s 12¯ SYMBOL 175 \f "Symbol" \s 12¯ ГSYMBOL 98 \f "Symbol" \s 12bSYMBOL 98 \f "Symbol" \s 12b 1 -1 SYMBOL 173 \f "Symbol" \s 12­ SYMBOL 173 \f "Symbol" \s 12­ ДSYMBOL 97 \f "Symbol" \s 12aSYMBOL 97 \f "Symbol" \s 12a 0 1 SYMBOL 173 \f "Symbol" \s 12­ SYMBOL 175 \f "Symbol" \s 12¯ ДSYMBOL 97 \f "Symbol" \s 12aSYMBOL 98 \f "Symbol" \s 12b 0 0 SYMBOL 175 \f "Symbol" \s 12¯ SYMBOL 173 \f "Symbol" \s 12­ ДSYMBOL 98 \f "Symbol" \s 12bSYMBOL 97 \f "Symbol" \s 12a 0 0 SYMBOL 175 \f "Symbol" \s 12¯ SYMBOL 175 \f "Symbol" \s 12¯ ДSYMBOL 98 \f "Symbol" \s 12bSYMBOL 98 \f "Symbol" \s 12b 0 -1 SYMBOL 173 \f "Symbol" \s 12­ SYMBOL 173 \f "Symbol" \s 12­ ЕSYMBOL 97 \f "Symbol" \s 12aSYMBOL 97 \f "Symbol" \s 12a -1 1 SYMBOL 173 \f "Symbol" \s 12­ SYMBOL 175 \f "Symbol" \s 12¯ ЕSYMBOL 97 \f "Symbol" \s 12aSYMBOL 98 \f "Symbol" \s 12b -1 0 SYMBOL 175 \f "Symbol" \s 12¯ SYMBOL 173 \f "Symbol" \s 12­ ЕSYMBOL 98 \f "Symbol" \s 12bSYMBOL 97 \f "Symbol" \s 12a -1 0 SYMBOL 175 \f "Symbol" \s 12¯ SYMBOL 175 \f "Symbol" \s 12¯ ЕSYMBOL 98 \f "Symbol" \s 12bSYMBOL 98 \f "Symbol" \s 12b -1 -1

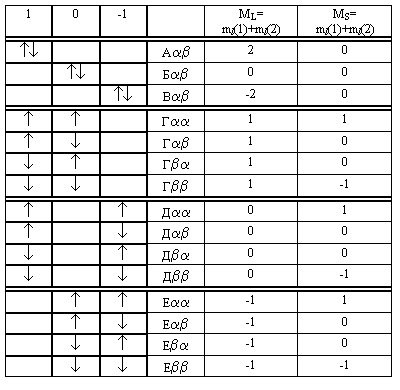С помощью двойки чисел (ML, MS) можно частично охарактеризовать микросостояние оболочки, но это ещё не исчерпывающая характеристика.