Контрольная работа на тему Обчислення матричних задач
Работа добавлена на сайт bukvasha.net: 2014-11-19Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ
Бердичівський політехнічний коледж
Контрольна робота
з дисципліни “Числові методи”
Виконав:
студент групи Пзс-503
Лифар Сергій Олександрович
Перевірив:
Федчук Людмила Олегівна
м. Бердичів 2009 р.
Завдання 2.
Завдання 3.
Завдання 4.
Список використаної літератури
Завдання 1
Обчислити визначник матриці методом Гаусса.
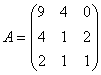
Розв'язок.
Визначник матриці А шукатимемо за формулою:
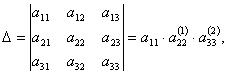
де 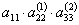
- ведучі елементи схеми єдиного ділення.
Складемо розрахункову таблицю і знайдемо 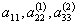
Отримаємо: de t= 9 · (-0,77778) · 1,285714 = -9
Завдання 2
Розгорнути характеристичний визначник заданої матриці методом Крилова.
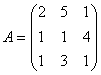
Розв'язок.
1. Вибираємо початковий вектор наближення 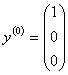
.
2. Визначаємо координати векторів
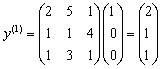
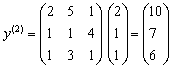
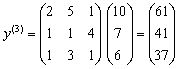
2. Визначаємо координати векторів
3. Складемо матричне рівняння:
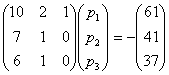
4. Запишемо систему виду.
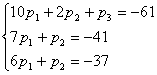
5. Розв’язавши систему методом Гауса, отримаємо
6. Таким чином, характеристичний визначник має вигляд:
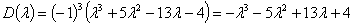
Завдання 3
Обчислити наближене значення визначеного інтегралу за допомогою формули Сімпсона, розбивши відрізок інтегрування на 10 частин. Усі обчислення проводити з точністю е=0,001.
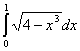
Розв'язок.
Наближене значення визначеного інтегралу методом Сімпсона обчислюється за формулою:
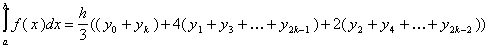
Крок табулювання функції знайдемо за формулою:
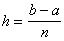
За умовою a=0 b=1 n=10, отже 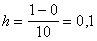
Складемо розрахункову таблицю значень функції змінюючи x від a до b на крок табулювання:
Знайдемо проміжкові суми з формули Сімпсона:
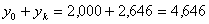
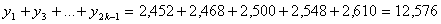
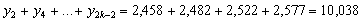
Отримуємо:
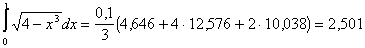
Завдання 4
Методом золотого перерізу знайти мінімум функції y=f(x) на відрізку [a; b] з точністю е=0,001.
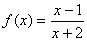
, [0; 4]; 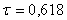
Розв'язок.
Найменше значення функції шукатиме за таким алгоритмом:
1) обчислюємо значення 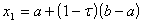
та 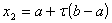
;
2) обчислюємо f(x1), f(x2);
3) якщо f(x1) ≤ f(x2), то для подальшого ділення залишаємо інтервал [a, x2];
4) якщо f(x1) > f(x2), то для подальшого ділення залишаємо інтервал [x1, b].
Процес ділення продовжуємо до тих пір, доки довжина інтервалу невизначеності не стане меншою заданої точності е.
Складемо розрахункову таблицю:
Отримали: 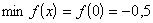
[0;4]
Список використаної літератури
1. Коссак О., Тумашова О. – Методи наближених обчислень: Навчальний посібник. Львів. 2003.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Вища математика в вправах та задачах. 1999.
3. Конспект лекцій.
Бердичівський політехнічний коледж
Контрольна робота
з дисципліни “Числові методи”
Виконав:
студент групи Пзс-503
Лифар Сергій Олександрович
Перевірив:
Федчук Людмила Олегівна
м. Бердичів 2009 р.
Зміст
Завдання 1.Завдання 2.
Завдання 3.
Завдання 4.
Список використаної літератури
Завдання 1
Обчислити визначник матриці методом Гаусса.
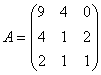
Розв'язок.
Визначник матриці А шукатимемо за формулою:
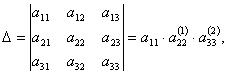
де
Складемо розрахункову таблицю і знайдемо
| Стовпчики | ||
| 1 | 2 | 3 |
| 9 | 4 | 0 |
| 4 | 1 | 2 |
| 2 | 1 | 1 |
| 1 | 0,44444 | 0 |
| -0,77778 | 2 | |
| 0,11111 | 1 | |
| 1 | -2,57143 | |
| 1,285714 | ||
Завдання 2
Розгорнути характеристичний визначник заданої матриці методом Крилова.
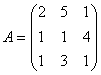
Розв'язок.
1. Вибираємо початковий вектор наближення
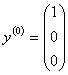
2. Визначаємо координати векторів
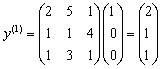
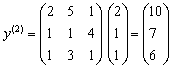
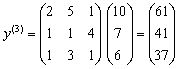
2. Визначаємо координати векторів
3. Складемо матричне рівняння:
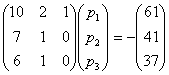
4. Запишемо систему виду.
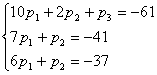
5. Розв’язавши систему методом Гауса, отримаємо
| p1 | p2 | p3 | b | У1 | У2 |
| 1 | 2 | 10 | -61 | -48 | |
| 0 | 1 | 7 | -41 | -33 | |
| 0 | 1 | 6 | -37 | -30 | |
| 1 | 2 | 10 | -61 | -48 | -48 |
| 1 | 7 | -41 | -33 | -33 | |
| 1 | 6 | -37 | -30 | -30 | |
| 1 | 7 | -41 | -33 | -33 | |
| -1 | 4 | 3 | 3 | ||
| 1 | -4 | -3 | -3 | ||
| 1 | p3 | -4 | |||
| 1 | p2 | -13 | |||
| 1 | p1 | 5 |
Завдання 3
Обчислити наближене значення визначеного інтегралу за допомогою формули Сімпсона, розбивши відрізок інтегрування на 10 частин. Усі обчислення проводити з точністю е=0,001.
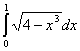
Розв'язок.
Наближене значення визначеного інтегралу методом Сімпсона обчислюється за формулою:
Крок табулювання функції знайдемо за формулою:
За умовою a=0 b=1 n=10, отже
Складемо розрахункову таблицю значень функції змінюючи x від a до b на крок табулювання:
| i | xi | f(xi) |
| 0 | 0 | 2,000 |
| 1 | 0,1 | 2,452 |
| 2 | 0,2 | 2,458 |
| 3 | 0,3 | 2,468 |
| 4 | 0,4 | 2,482 |
| 5 | 0,5 | 2,500 |
| 6 | 0,6 | 2,522 |
| 7 | 0,7 | 2,548 |
| 8 | 0,8 | 2,577 |
| 9 | 0,9 | 2,610 |
| 10 | 1 | 2,646 |
Отримуємо:
Завдання 4
Методом золотого перерізу знайти мінімум функції y=f(x) на відрізку [a; b] з точністю е=0,001.
Розв'язок.
Найменше значення функції шукатиме за таким алгоритмом:
1) обчислюємо значення
2) обчислюємо f(x1), f(x2);
3) якщо f(x1) ≤ f(x2), то для подальшого ділення залишаємо інтервал [a, x2];
4) якщо f(x1) > f(x2), то для подальшого ділення залишаємо інтервал [x1, b].
Процес ділення продовжуємо до тих пір, доки довжина інтервалу невизначеності не стане меншою заданої точності е.
Складемо розрахункову таблицю:
| a | b | x1 | x2 | f(x1) | f(x2) |
| 0,000 | 4,000 | 1,528 | 2,472 | 0,150 | 0,329 |
| 0,000 | 2,472 | 0,944 | 1,528 | -0,019 | 0,150 |
| 0,000 | 1,528 | 0,584 | 0,944 | -0,161 | -0,019 |
| 0,000 | 0,944 | 0,361 | 0,583 | -0,271 | -0,161 |
| 0,000 | 0,583 | 0,223 | 0,361 | -0,350 | -0,271 |
| 0,000 | 0,361 | 0,138 | 0,023 | -0,403 | -0,350 |
| 0,000 | 0,223 | 0,085 | 0,138 | -0,439 | -0,403 |
| 0,000 | 0,138 | 0,053 | 0,085 | -0,462 | -0,439 |
| 0,000 | 0,085 | 0,033 | 0,053 | -0,476 | -0,462 |
| 0,000 | 0,053 | 0,020 | 0,033 | -0,485 | -0,476 |
| 0,000 | 0,033 | 0,012 | 0,020 | -0,491 | -0,45 |
| 0,000 | 0,020 | 0,008 | 0,012 | -0,494 | -0,491 |
| 0,000 | 0,012 | 0,005 | 0,008 | -0,496 | -0,494 |
| 0,000 | 0,002 | 0,003 | 0,005 | -0,498 | -0,496 |
| 0,000 | 0,005 | 0,002 | 0,003 | -0,499 | -0,498 |
[0;4]
Список використаної літератури
1. Коссак О., Тумашова О. – Методи наближених обчислень: Навчальний посібник. Львів. 2003.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Вища математика в вправах та задачах. 1999.
3. Конспект лекцій.