Курсовая на тему Теплопроводность твердых тел
Работа добавлена на сайт bukvasha.net: 2014-07-16Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
ОГЛАВЛЕНИЕ
Введение
Глава 1. Нормальные колебания атомов решетки
Глава 2. Теплопроводность кристаллической решетки твердого тела
Глава 3. Фононы. Фононный газ
Глава 4. Электронная теплопроводность.
Заключение
Список использованной литературы
ВВЕДЕНИЕ
Тепловое движение частиц твердого тела, как конденсированной среды, отлично от движения частиц газов. В основу теории твердого тела положена модель бесконечного идеального монокристалла. Частицы твердого тела, связанные между собой силами взаимодействия, которые зависят от расстояния, совершают колебания около положений равновесия в узлах кристаллической решетки. На основе этого и разработана теория теплоемкости и теплопроводности твердого тела. Знание величин теплоемкости и коэффициента теплопроводности твердого тела необходимо для инженерных расчетов при создании новых машин, расчете их коэффициента полезного действия, они нужны в строительстве для расчета тепловых свойств строений, их теплоизоляционных свойств. В общем случае перенос тепла осуществляется двумя типами носителей: электронами проводимости и собственно фононами. Рассмотрим основные механизмы переноса тепла в твердом теле.
ГЛАВА 1.
НОРМАЛЬНЫЕ КОЛЕБАНИЯ АТОМОВ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ.
Каждое нормальное колебание несет в себе энергию и импульс, а следовательно могут характеризоваться этими параметрами (энергией и импульсом). Можно доказать, что энергия отдельного нормального колебания кристаллической решетки равна энергии гармонического осциллятора, который имеет массу равную массе всех атомов кристаллической решетки участвующих в данных колебаниях и колеблющегося с частотой равной частоте нормальных колебаний, а следовательно полная энергия кристалла из N атомов равна 3N гармонических осцилляторов.
Энергия каждого колебания квантована. Минимальная порция или квант энергии колебания называется фононом. Энергия фонона:
Еф = `h w.
В зависимости от частоты (l) фононы бывают акустическими и оптическими.
Для описания процессов, связанных с упругими колебаниями, КР представляют в виде фононного газа. Увеличение энергии колебаний означает увеличение концентрации фононов nф. Рассеяние одной упругой волны на другой - фонон-фононное взаимодействие. Рассеяние упругой волны на дефектах КР - взаимодействие фонона с дефектом.
Максимальная частота колебаний атомов в кристалле называется характеристической или дебаевской wD частотой . Она определяет характеристическую или дебаевскую температуру - ту температуру, при которой в образце возбуждаются все возможные нормальные колебания вплоть до частоты wD:
QD = wD `h / k. (`h = h / 2π ),
где h – постоянная Планка, k – постоянная Больцмана.
Дебаевская температура QD используется как критерий величины температуры тела:
T > QD считаются высокоми , T < QD - низкими.
Т.е. при T > QD не возникает новых нормальных колебаний, а лишь увеличивается амплитуда существующих.
Передача тепловой энергии в неравномерно нагретом веществе (без теплового излучения) характеризуется теплопроводностью. В соответствии с законом Фурье , если в веществе имеется градиент температуры Ñ Т, то в направлении, противоположном ÑТ, возникает пропорциональный поток энергии плотностью:
jт = - K ÑT,
где К - коэффициент теплопроводности, [ Вт/ м град ] .
Перенос тепла осуществляется за счет фононной и электронной теплопроводности:
К = Кф + Кэл .
Для фононов
Кф = 1/3 Сф lф Vф,
где lф - длина свободного пробега фононов , обратно пропорциональная концентрации фононов nф, Vф - скорость фононов (скорость звука)
Vф = Vзв = Ö` Е/r ,
Е - модуль упругости Юнга, r - плотность вещества.
Теплопроводность прямо пропорционально зависит от энергии связи Есв (степени жесткости связи): чем больше Есв , тем больше модуль Е и, следовательно, скорость звука Vзв . В отсутствии электронной теплопроводности передача тепловой энергии от одних точек тела к другим осуществляется только фононами [3].
Теория переноса тепла фононами находится в такой стадии, когда по ней еще нельзя установить количественную зависимость решеточной (фононной) теплопроводности от температуры. Поэтому для практических целей необходимо найти зависимость теплопроводности от температуры в виде эмпирических формул. 
В передаче энергии, по нашему мнению, участвуют только фононы с энергией. Перенос энергии фононами происходит путем их переброса от осцилляторов с энергией hυ0 к осцилляторам с меньшей энергией. В процессе переброса фононы с энергией  могут дробиться на фононы с меньшей энергией.
могут дробиться на фононы с меньшей энергией.
Как известно, коэффициент теплового расширения обусловлен силами ангармонического взаимодействия между атомами. Однако, силы ангармонического взаимодействия- это только один из факторов, оказывающих влияние на решеточную теплопроводность.
Концентрация фононов n с энергией  зависит только от температуры и описывается функцией распределения фононов от температуры. Такой характер температурной зависимости теплопроводности при низких температурах вызван наложением двух процессов: с одной стороны, резким снижением ангармонической составляющей сопротивления перемещению электронов и фононов, с другой,- уменьшением по экспоненте числа фононов способных принимать участие в процессах переброса энергии от одних точек к другим. На рисунках приведены зависимости теплопроводности металла (германия) от температуры в области низких температур а также зависимость теплопроводности алмаза в области от 0К до 300К. Эти зависимости имеют стандартный характер.
зависит только от температуры и описывается функцией распределения фононов от температуры. Такой характер температурной зависимости теплопроводности при низких температурах вызван наложением двух процессов: с одной стороны, резким снижением ангармонической составляющей сопротивления перемещению электронов и фононов, с другой,- уменьшением по экспоненте числа фононов способных принимать участие в процессах переброса энергии от одних точек к другим. На рисунках приведены зависимости теплопроводности металла (германия) от температуры в области низких температур а также зависимость теплопроводности алмаза в области от 0К до 300К. Эти зависимости имеют стандартный характер.

Рис. 1(2). Зависимость теплопроводности Ge от температуры (при низких температурах), полученная из опыта и рассчитанная по формуле.

Рис. 1(2). Зависимость теплопроводности алмаза от температуры (при низких температурах), полученная из опыта и рассчитанная по формуле.
ГЛАВА 2. ТЕПЛОПРОВОДНОСТЬ КРИСТАЛЛИЧЕСКОЙ
РЕШЕТКИ ТВЕРДОГО ТЕЛА.
Тепловая энергия содержится в колебательных нормальных модах кристалла. В диэлектриках этот механизм является основным, поскольку свободных электронов в диэлектриках нет. При низких температурах разрешенные энергии нормальных мод квантованы и передача энергии, сопровождающая теплопроводность, осуществляется через механизм, описываемый в представлении о фононах.
В идеальном гармоническом кристалле фононные состояния считаются стационарными. Поэтому, если установилось некоторое распределение фононов с направленными в одну сторону групповыми скоростями, то это распределение не будет меняться с течением времени, так что поток тепла не будет затухать. Т.е. идеальный гармонический кристалл имел бы бесконечную теплопроводность. Помимо несовершенств решетки, играющих роль рассеивающих центров, теплопроводность реальных диэлектриков принимает конечные значения из-за ангармонизма колебаний решетки.
В отличие от гармонической, в ангармонической модели волны могут взаимодействовать. На квантовом языке - фононы могут рассеиваться с рождением и поглощением фононов. В процессах 3-го порядка фонон может распасться на два других, либо два фонона могут слиться и образовать третий. В процессах 4-го порядка участвуют 4 фонона. Т.е. один фонон может распасться на три, либо три фонона могут слиться с образованием одного, либо два фонона могут рассеяться друг на друге и сформироваться два новых. Все эти и аналогичные процессы более высокого порядка называются рассеянием, либо столкновением, либо переходами фононов. Теплопроводность металлов должна складываться из теплопроводности фононной (теплопроводность решетки) и электронной подсистем:  =
=  lat +
lat +  e. Однако механизм решеточной теплопроводности в металлах в значительной мере маскируется электронным механизмом переноса тепла.
e. Однако механизм решеточной теплопроводности в металлах в значительной мере маскируется электронным механизмом переноса тепла.
ГЛАВА 3. ФОНОНЫ. ФОНОННЫЙ ГАЗ.
Квантовый гармонический осциллятор имеет энергию равную:
 где n = 1, 2, 3 … (3.1)
где n = 1, 2, 3 … (3.1)
Минимальная порция энергии которую может  поглотить или испустить кристаллическая решетка при тепловых колебаниях соответствует на этом рисунке переходу с одного энергетического уровня на другой равна
поглотить или испустить кристаллическая решетка при тепловых колебаниях соответствует на этом рисунке переходу с одного энергетического уровня на другой равна  и называется фононом.
и называется фононом.
Таким образом между светом и тепловыми колебаниями кристаллической решетки можно провести аналогию - упругие волны рассматриваются как распространение неких квазиупругих частиц – фононов.
Упругие волны рассматриваются как распространение неких квазичастиц – фононов. Для которых можно записать величину их импульса и энергии:
 , где q – волновое число. (3.2)
, где q – волновое число. (3.2)
Р. Паерлс в 1029 году ввел в теорию Дебая квантовые ( фононные ) явления ы показал, что тепловое сопротивление решетки обусловлено взаимодействием фононов. Фонон, в отличии от обычных частиц, может существовать лишь в некоторой среде, которая пребывает в состоянии теплового возбуждения. Нельзя вообразить фонон, который распространялся бы в вакууме, поскольку он описывает квантовый характер тепловых колебаний решетки и навечно замкнут в кристалле. Понятие фонона – исторически первой квазичистицы в квантовой теории твердого тела ввел И. Е. Тамм. Корпускулярный аспект малых колебаний атомов решетки кристалла приводит к понятию фонона, и распространение упругих тепловых волн в кристалле можно рассматривать как перенесение фононов.
Тепловые колебания в кристаллической решетки являются термическим возбуждением фононов. Для определения средней энергии кристаллической решетки нужно найти среднюю энергию гармонического осциллятора:
 - энергия квантового гармонического осциллятора (3.3).
- энергия квантового гармонического осциллятора (3.3).
Если учесть квантовую природу гармонического осцилятора, то для тела, которое состоит из N атомов можно записать его внутреннюю энергию, где на каждую степень Володи атома будет приходится энергия равная средней энергии квантового осцилятора: 
(3.4)
Наиболее простой моделью для анализа температурной зависимости теплопроводности является модель газа фононов (МГФ). МГФ оперирует с такими понятиями, как средняя длина свободного пробега фонона 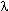 ph, эффективное время релаксации
ph, эффективное время релаксации  =
= 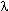 ph/vs, обратной величиной которого, 1/
ph/vs, обратной величиной которого, 1/  , является средняя частота столкновений фононов. Величина теплопроводности в модели фононного газа равна:
, является средняя частота столкновений фононов. Величина теплопроводности в модели фононного газа равна:
 lat = 1/3
lat = 1/3 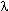 phvsCv = 1/3 vs2
phvsCv = 1/3 vs2  Cv, (3.5)
Cv, (3.5)
где Сv удельная теплоемкость, связанная с колебаниями решетки. Величины Сv,  или
или 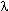 ph определяют температурную зависимость решеточной теплопроводности. Зависимость
ph определяют температурную зависимость решеточной теплопроводности. Зависимость  от Т оказалась более сложной. Рассмотрим два случая.
от Т оказалась более сложной. Рассмотрим два случая.
а) Т >>  D. Следовательно, длина свободного пробега фонона
D. Следовательно, длина свободного пробега фонона 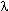 обратно пропорциональна температуре. Это согласуется с экспериментом. Обычно,
обратно пропорциональна температуре. Это согласуется с экспериментом. Обычно,  lat ~ 1/Tx, где х = 1-2. Точная теория
lat ~ 1/Tx, где х = 1-2. Точная теория  lat(Т) должна учитывать конкуренцию между процессами. б) Т<<
lat(Т) должна учитывать конкуренцию между процессами. б) Т<<  D. В этом случае фононы будут иметь энергию
D. В этом случае фононы будут иметь энергию 
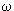 s(k)
s(k) 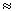 kBT << kB
kBT << kB  D =
D = 
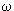 D, т.е.
D, т.е. 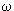 s <<
s << 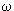 D и k << kD. Можно считать, что как до, так и после рассеяния, энергия как отдельного фонона, так и суммарная энергия остаются <<
D и k << kD. Можно считать, что как до, так и после рассеяния, энергия как отдельного фонона, так и суммарная энергия остаются << 
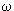 D, волновой вектор << kD. Следовательно, если в начальный момент система фононов имела некоторый результирующий импульс, то этот импульс будет сохраняться даже в отсутствие градиента температуры, т.е. для совершенного бесконечного ангармонического кристалла при низких температурах теплопроводность бесконечна, точнее она может быть конечной только лишь за счет небольшой вероятности процессов переброса, нарушающих закон сохранения квазиимпульса, и которые уменьшают тепловой поток.
D, волновой вектор << kD. Следовательно, если в начальный момент система фононов имела некоторый результирующий импульс, то этот импульс будет сохраняться даже в отсутствие градиента температуры, т.е. для совершенного бесконечного ангармонического кристалла при низких температурах теплопроводность бесконечна, точнее она может быть конечной только лишь за счет небольшой вероятности процессов переброса, нарушающих закон сохранения квазиимпульса, и которые уменьшают тепловой поток.
При достижении температуры, где начинаются рост времени релаксации и, соответственно, длины свободного пробега фононов, теплопроводность решетки растет (подтверждается экспериментально). При дальнейшем снижении Т, длина свободного пробега становится сопоставимой со средней длиной свободного пробега, характеризующей рассеяние фононов на дефектах решетки, примесях или даже на торцах конечного образца. Для диэлектриков при очень низких температурах, Т<Tmax, теплопроводность  ~ T3 , затем Tmax < Т <
~ T3 , затем Tmax < Т <  D
D  ~ exp(T0/T), далее темп уменьшения спадает и заменяется медленным спаданием
~ exp(T0/T), далее темп уменьшения спадает и заменяется медленным спаданием  ~ 1/T из-за увеличения числа рассеивающих фононов.
~ 1/T из-за увеличения числа рассеивающих фононов.
ГЛАВА 4. ЭЛЕКТРОННАЯ ТЕПЛОПРОВОДНОСТЬ.
В металлах значительную роль в процессе теплопроводимости играет электронная теплопроводимость. Она также существует и в полупроводниках, особенно легированных электронодонорными элементами. По величине электронная теплопроводность и фононная теплопроводности в металлах будут равны:
Сэл/Сф » 0.01 , Vзв » 5 ·103 м/с, Vт » 106 м/с ,
lф » 10-9 м , lэл » 10-8 м ,
Кф / Кэл » 0.05.
В чистых металлах электронная теплопроводность больше за фононную в 20 раз. В сплавах фононная и электронная теплопроводности приблизительно равны. Например, бериллий Ве с низкой электропроводностью обладает теплопроводностью в 5 раз большей, чем у стали. Ве входит в состав теплопроводящих паст и подложек для мощных усилителей и генераторов.
В результате взаимодействия фононов между собой и с электронами рассеивается энергия. Это взаимодействие интерпретируется как тепловое сопротивление RT :

(4.1)
где L и S - длина и площадь образца или фрагмента конструкции.
Расчет теплового сопротивления сложной детали проводится по правилам, аналогичным законам Ома.
Коэффициент тепло проводимости для электронного газа в металех имеет значение:
Кэл = 
Сэл lэл Vт , (4.2)
где Сэл – теплоемкость электронного газа, lэл - длина свободного пробега электрона, Vт - тепловая скорость:

, где mе - масса электрона.
Особую сложность при использовании формулы (4.2) представляет вычисление величины длинны свободного пробега электрона, поскольку это величина статистическая и зависит от движения других электронов в металле.
Электронная теплопроводность запишется:
 (4.3)
(4.3)
 , (4.4)
, (4.4)
где  .
.
При температурах выше комнатной для большинства металлов можно сделать следующее допущение

, (4.5) 
Формула для электронной теплопроводности принимает вид:
 (4.6)
(4.6)
Формула (4.6) совпадает с законом Видемана-Франца.
Таким образом, пользоваться законом Видемана-Франца при расчете теплопроводности металлов можно только при температуре выше температуры Дебая. При температурах ниже температуры Дебая использование закона Видемана-Франца приведет к большим неточностям при вычислении теплопроводности металлов.
Характерный вид кривой зависимости λ(Т) приведен на рисунке 4.1. теоретические и экспериментальные исследования показали, что тепло проводимость кристаллических веществ в области максимума λ(Т) довольно сильно зависит от дефектов кристаллической решетки.

Рис. 4.1. Температурная зависимость коэффициента электронной теплопроводности.
I - Увеличивается тепловая скорость Vт.
II - Cущественно уменьшается длина свободного пробега lэл из-за роста концентрации фононов в результате электрон-фононного взаимодействия. При Т<< θD вероятность рассеивания фононов уменьшается за экспонентой, что приводит к быстрому росту теплопроводности: 
.
Ш - При высоких температурах устанавливается баланс между lэл и nф , электронная теплопроводность практически не зависит от температуры. При этом величины Сэл и Vт можно считать постоянными.
ЗАКЛЮЧЕНИЕ.
Теория теплопроводности твердого тела на сегодняшний день разработана недостаточно. Она прекрасно справилась с объяснением теоретических вопросов теплопроводности, ее зависимости от температуры в разных температурных диапазонах, но она не может пока что дать возможность вычислить теплопроводность разных материалов с достаточной точностью. Наибольшую сложность для вычисления теплопроводности представляют диэлектрические материалы, ведь теплопроводности кристаллических и аморфных тел значительно отличаются между собой. Это связано с отсутствием в аморфных телах трансляционной симметрии («дальнего порядка»). Качественно отличный также характер зависимостей λ(Т). Для аморфных тел максимум на кривых λ (Т) не наблюдается, для них характерно увеличение λ с повышением температуры Т. При высоких температурах λ стремится к насыщению. Значение описывается формулой Дебая:

, lФ равняется приблизительно расстоянию между структурными частицами аморфного тела. Но точное вычисление длины свободного пробега на данный момент невозможно.
Поэтому теория теплопроводимости в наше время активно развивается.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Дущенко В. П., Кучерук И. М. Общая физика. – К.: Высшая школа, 1995. – 430 с.
2. Зисман Г. А., Тодес О. М. Курс общей физики. В 3 т. – М.: Наука, 1995. – 343 с.
3. Кухлинг Х. Справочник по физике: Пер. с нем. – М.: Мир, 1983. – 520 с.
4. Яворский Б. М., Детлаф А. А. Справочник по физике. – М.: Наука, 1982. – 846 с.
5. Шебалин О. Д. Физические основы механики. – М.: Высшая школа, 1981. – 263 с.
Введение
Глава 1. Нормальные колебания атомов решетки
Глава 2. Теплопроводность кристаллической решетки твердого тела
Глава 3. Фононы. Фононный газ
Глава 4. Электронная теплопроводность.
Заключение
Список использованной литературы
ВВЕДЕНИЕ
Тепловое движение частиц твердого тела, как конденсированной среды, отлично от движения частиц газов. В основу теории твердого тела положена модель бесконечного идеального монокристалла. Частицы твердого тела, связанные между собой силами взаимодействия, которые зависят от расстояния, совершают колебания около положений равновесия в узлах кристаллической решетки. На основе этого и разработана теория теплоемкости и теплопроводности твердого тела. Знание величин теплоемкости и коэффициента теплопроводности твердого тела необходимо для инженерных расчетов при создании новых машин, расчете их коэффициента полезного действия, они нужны в строительстве для расчета тепловых свойств строений, их теплоизоляционных свойств. В общем случае перенос тепла осуществляется двумя типами носителей: электронами проводимости и собственно фононами. Рассмотрим основные механизмы переноса тепла в твердом теле.
ГЛАВА 1.
НОРМАЛЬНЫЕ КОЛЕБАНИЯ АТОМОВ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ.
Каждое нормальное колебание несет в себе энергию и импульс, а следовательно могут характеризоваться этими параметрами (энергией и импульсом). Можно доказать, что энергия отдельного нормального колебания кристаллической решетки равна энергии гармонического осциллятора, который имеет массу равную массе всех атомов кристаллической решетки участвующих в данных колебаниях и колеблющегося с частотой равной частоте нормальных колебаний, а следовательно полная энергия кристалла из N атомов равна 3N гармонических осцилляторов.
Энергия каждого колебания квантована. Минимальная порция или квант энергии колебания называется фононом. Энергия фонона:
Еф = `h w.
В зависимости от частоты (l) фононы бывают акустическими и оптическими.
Для описания процессов, связанных с упругими колебаниями, КР представляют в виде фононного газа. Увеличение энергии колебаний означает увеличение концентрации фононов nф. Рассеяние одной упругой волны на другой - фонон-фононное взаимодействие. Рассеяние упругой волны на дефектах КР - взаимодействие фонона с дефектом.
Максимальная частота колебаний атомов в кристалле называется характеристической или дебаевской wD частотой . Она определяет характеристическую или дебаевскую температуру - ту температуру, при которой в образце возбуждаются все возможные нормальные колебания вплоть до частоты wD:
QD = wD `h / k. (`h = h / 2π ),
где h – постоянная Планка, k – постоянная Больцмана.
Дебаевская температура QD используется как критерий величины температуры тела:
T > QD считаются высокоми , T < QD - низкими.
Т.е. при T > QD не возникает новых нормальных колебаний, а лишь увеличивается амплитуда существующих.
Передача тепловой энергии в неравномерно нагретом веществе (без теплового излучения) характеризуется теплопроводностью. В соответствии с законом Фурье , если в веществе имеется градиент температуры Ñ Т, то в направлении, противоположном ÑТ, возникает пропорциональный поток энергии плотностью:
jт = - K ÑT,
где К - коэффициент теплопроводности, [ Вт/ м град ] .
Перенос тепла осуществляется за счет фононной и электронной теплопроводности:
К = Кф + Кэл .
Для фононов
Кф = 1/3 Сф lф Vф,
где lф - длина свободного пробега фононов , обратно пропорциональная концентрации фононов nф, Vф - скорость фононов (скорость звука)
Vф = Vзв = Ö` Е/r ,
Е - модуль упругости Юнга, r - плотность вещества.
Теплопроводность прямо пропорционально зависит от энергии связи Есв (степени жесткости связи): чем больше Есв , тем больше модуль Е и, следовательно, скорость звука Vзв . В отсутствии электронной теплопроводности передача тепловой энергии от одних точек тела к другим осуществляется только фононами [3].
Теория переноса тепла фононами находится в такой стадии, когда по ней еще нельзя установить количественную зависимость решеточной (фононной) теплопроводности от температуры. Поэтому для практических целей необходимо найти зависимость теплопроводности от температуры в виде эмпирических формул.

В передаче энергии, по нашему мнению, участвуют только фононы с энергией. Перенос энергии фононами происходит путем их переброса от осцилляторов с энергией hυ0 к осцилляторам с меньшей энергией. В процессе переброса фононы с энергией
Как известно, коэффициент теплового расширения обусловлен силами ангармонического взаимодействия между атомами. Однако, силы ангармонического взаимодействия- это только один из факторов, оказывающих влияние на решеточную теплопроводность.
Концентрация фононов n с энергией

Рис. 1(2). Зависимость теплопроводности Ge от температуры (при низких температурах), полученная из опыта и рассчитанная по формуле.

Рис. 1(2). Зависимость теплопроводности алмаза от температуры (при низких температурах), полученная из опыта и рассчитанная по формуле.
ГЛАВА 2. ТЕПЛОПРОВОДНОСТЬ КРИСТАЛЛИЧЕСКОЙ
РЕШЕТКИ ТВЕРДОГО ТЕЛА.
Тепловая энергия содержится в колебательных нормальных модах кристалла. В диэлектриках этот механизм является основным, поскольку свободных электронов в диэлектриках нет. При низких температурах разрешенные энергии нормальных мод квантованы и передача энергии, сопровождающая теплопроводность, осуществляется через механизм, описываемый в представлении о фононах.
В идеальном гармоническом кристалле фононные состояния считаются стационарными. Поэтому, если установилось некоторое распределение фононов с направленными в одну сторону групповыми скоростями, то это распределение не будет меняться с течением времени, так что поток тепла не будет затухать. Т.е. идеальный гармонический кристалл имел бы бесконечную теплопроводность. Помимо несовершенств решетки, играющих роль рассеивающих центров, теплопроводность реальных диэлектриков принимает конечные значения из-за ангармонизма колебаний решетки.
В отличие от гармонической, в ангармонической модели волны могут взаимодействовать. На квантовом языке - фононы могут рассеиваться с рождением и поглощением фононов. В процессах 3-го порядка фонон может распасться на два других, либо два фонона могут слиться и образовать третий. В процессах 4-го порядка участвуют 4 фонона. Т.е. один фонон может распасться на три, либо три фонона могут слиться с образованием одного, либо два фонона могут рассеяться друг на друге и сформироваться два новых. Все эти и аналогичные процессы более высокого порядка называются рассеянием, либо столкновением, либо переходами фононов. Теплопроводность металлов должна складываться из теплопроводности фононной (теплопроводность решетки) и электронной подсистем:
ГЛАВА 3. ФОНОНЫ. ФОНОННЫЙ ГАЗ.
Квантовый гармонический осциллятор имеет энергию равную:
Минимальная порция энергии которую может
 поглотить или испустить кристаллическая решетка при тепловых колебаниях соответствует на этом рисунке переходу с одного энергетического уровня на другой равна
поглотить или испустить кристаллическая решетка при тепловых колебаниях соответствует на этом рисунке переходу с одного энергетического уровня на другой равна Таким образом между светом и тепловыми колебаниями кристаллической решетки можно провести аналогию - упругие волны рассматриваются как распространение неких квазиупругих частиц – фононов.
Упругие волны рассматриваются как распространение неких квазичастиц – фононов. Для которых можно записать величину их импульса и энергии:
Р. Паерлс в 1029 году ввел в теорию Дебая квантовые ( фононные ) явления ы показал, что тепловое сопротивление решетки обусловлено взаимодействием фононов. Фонон, в отличии от обычных частиц, может существовать лишь в некоторой среде, которая пребывает в состоянии теплового возбуждения. Нельзя вообразить фонон, который распространялся бы в вакууме, поскольку он описывает квантовый характер тепловых колебаний решетки и навечно замкнут в кристалле. Понятие фонона – исторически первой квазичистицы в квантовой теории твердого тела ввел И. Е. Тамм. Корпускулярный аспект малых колебаний атомов решетки кристалла приводит к понятию фонона, и распространение упругих тепловых волн в кристалле можно рассматривать как перенесение фононов.
Тепловые колебания в кристаллической решетки являются термическим возбуждением фононов. Для определения средней энергии кристаллической решетки нужно найти среднюю энергию гармонического осциллятора:
 - энергия квантового гармонического осциллятора (3.3).
- энергия квантового гармонического осциллятора (3.3). Если учесть квантовую природу гармонического осцилятора, то для тела, которое состоит из N атомов можно записать его внутреннюю энергию, где на каждую степень Володи атома будет приходится энергия равная средней энергии квантового осцилятора:

(3.4)
Наиболее простой моделью для анализа температурной зависимости теплопроводности является модель газа фононов (МГФ). МГФ оперирует с такими понятиями, как средняя длина свободного пробега фонона
где Сv удельная теплоемкость, связанная с колебаниями решетки. Величины Сv,
а) Т >>
При достижении температуры, где начинаются рост времени релаксации и, соответственно, длины свободного пробега фононов, теплопроводность решетки растет (подтверждается экспериментально). При дальнейшем снижении Т, длина свободного пробега становится сопоставимой со средней длиной свободного пробега, характеризующей рассеяние фононов на дефектах решетки, примесях или даже на торцах конечного образца. Для диэлектриков при очень низких температурах, Т<Tmax, теплопроводность
ГЛАВА 4. ЭЛЕКТРОННАЯ ТЕПЛОПРОВОДНОСТЬ.
В металлах значительную роль в процессе теплопроводимости играет электронная теплопроводимость. Она также существует и в полупроводниках, особенно легированных электронодонорными элементами. По величине электронная теплопроводность и фононная теплопроводности в металлах будут равны:
Сэл/Сф » 0.01 , Vзв » 5 ·103 м/с, Vт » 106 м/с ,
lф » 10-
Кф / Кэл » 0.05.
В чистых металлах электронная теплопроводность больше за фононную в 20 раз. В сплавах фононная и электронная теплопроводности приблизительно равны. Например, бериллий Ве с низкой электропроводностью обладает теплопроводностью в 5 раз большей, чем у стали. Ве входит в состав теплопроводящих паст и подложек для мощных усилителей и генераторов.
В результате взаимодействия фононов между собой и с электронами рассеивается энергия. Это взаимодействие интерпретируется как тепловое сопротивление RT :
где L и S - длина и площадь образца или фрагмента конструкции.
Расчет теплового сопротивления сложной детали проводится по правилам, аналогичным законам Ома.
Коэффициент тепло проводимости для электронного газа в металех имеет значение:
Кэл =
где Сэл – теплоемкость электронного газа, lэл - длина свободного пробега электрона, Vт - тепловая скорость:

Особую сложность при использовании формулы (4.2) представляет вычисление величины длинны свободного пробега электрона, поскольку это величина статистическая и зависит от движения других электронов в металле.
Электронная теплопроводность запишется:
 (4.3)
(4.3)  , (4.4)
, (4.4) где
При температурах выше комнатной для большинства металлов можно сделать следующее допущение

, (4.5)
Формула для электронной теплопроводности принимает вид:
Формула (4.6) совпадает с законом Видемана-Франца.
Таким образом, пользоваться законом Видемана-Франца при расчете теплопроводности металлов можно только при температуре выше температуры Дебая. При температурах ниже температуры Дебая использование закона Видемана-Франца приведет к большим неточностям при вычислении теплопроводности металлов.
Характерный вид кривой зависимости λ(Т) приведен на рисунке 4.1. теоретические и экспериментальные исследования показали, что тепло проводимость кристаллических веществ в области максимума λ(Т) довольно сильно зависит от дефектов кристаллической решетки.

Рис. 4.1. Температурная зависимость коэффициента электронной теплопроводности.
I - Увеличивается тепловая скорость Vт.
II - Cущественно уменьшается длина свободного пробега lэл из-за роста концентрации фононов в результате электрон-фононного взаимодействия. При Т<< θD вероятность рассеивания фононов уменьшается за экспонентой, что приводит к быстрому росту теплопроводности:
Ш - При высоких температурах устанавливается баланс между lэл и nф , электронная теплопроводность практически не зависит от температуры. При этом величины Сэл и Vт можно считать постоянными.
ЗАКЛЮЧЕНИЕ.
Теория теплопроводности твердого тела на сегодняшний день разработана недостаточно. Она прекрасно справилась с объяснением теоретических вопросов теплопроводности, ее зависимости от температуры в разных температурных диапазонах, но она не может пока что дать возможность вычислить теплопроводность разных материалов с достаточной точностью. Наибольшую сложность для вычисления теплопроводности представляют диэлектрические материалы, ведь теплопроводности кристаллических и аморфных тел значительно отличаются между собой. Это связано с отсутствием в аморфных телах трансляционной симметрии («дальнего порядка»). Качественно отличный также характер зависимостей λ(Т). Для аморфных тел максимум на кривых λ (Т) не наблюдается, для них характерно увеличение λ с повышением температуры Т. При высоких температурах λ стремится к насыщению. Значение описывается формулой Дебая:
Поэтому теория теплопроводимости в наше время активно развивается.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Дущенко В. П., Кучерук И. М. Общая физика. – К.: Высшая школа, 1995. – 430 с.
2. Зисман Г. А., Тодес О. М. Курс общей физики. В 3 т. – М.: Наука, 1995. – 343 с.
3. Кухлинг Х. Справочник по физике: Пер. с нем. – М.: Мир, 1983. – 520 с.
4. Яворский Б. М., Детлаф А. А. Справочник по физике. – М.: Наука, 1982. – 846 с.
5. Шебалин О. Д. Физические основы механики. – М.: Высшая школа, 1981. – 263 с.