Курсовая на тему Численное интегрирование методом Гаусса
Работа добавлена на сайт bukvasha.net: 2014-12-01Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
КУРСОВАЯ РАБОТА
“Численное интегрирование методом Гаусса”
Федеральное агентство по образованию
Тульский государственный университет
КАФЕДРА РАДИОЭЛЕКТРОНИКИ
ИНФОРМАТИКА
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Вариант № 42
Студенту гр.220371 Подобеденко И.В.
1. Тема: "Численное интегрирование-методом Гаусса"
Разработайте алгоритм и программу:
1) вычисления определённого интеграла методом Гаусса и 2) построения графика функции я 3) построения нескольких (по 2 - 3) “шагов” интегрирования на участках возрастания и убывания функции.
Контрольный пример.
Исходные данные: 
2. Срок представления курсовой работы на проверку с 12 по 15 мая 2008 г.
3. Защита курсовой работы с 19 по 23 мая 2008 г.
4. Требования к курсовой работе:
3.1 Разработать алгоритм и программу решения поставленной задачи.
3.2 Язык программирования - Паскаль.
3.3 Предусмотреть: а) диалоговый ввод исходных данных с проверкой правильности вводимых величин, б) блок пояснений к работе с программой, в) решение контрольного примера.
5. Форма отчётности:
пояснительная записка (ПЗ) объёмом 25-40 страниц на листах с рамками и штампом, отпечатанная на принтере,
графическая часть - лист формата А1,
дискета с текстом ПЗ, рисунком алгоритма и программой (текстовый и исполняемый файлы).
6. Содержание пояснительной записки к курсовой работе:
1) титульный лист,
2) задание на курсовую работу (настоявши бланк).
3) аннотация (краткая характеристика проделанной работы, объём ПЗ, количество таблиц, рисунков, схем. программ и приложений) с основной надписью по форме 2 (ГОСТ 2.104-68) - 1 с,
4) содержание (лист содержания и все последующие листы - с основной надписью по форме 2а - ГОСТ 2.104-68),
5) введение (область применения поставленной задачи, возможность использования ЭВМ для решения поставленной задачи) – 1-2 с,
6) анализ задания (выбор входных и выходных данных) – 2-3 с.
7) обзор литературных источников и разработка (выбор) математической модели задачи – 2-4 с,
8) описание методов вычислительной математики, которые будут использованы при решении поставленной задачи - 3-4 с,
9) разработка алгоритма решения задачи и описание его особенностей (разработанных или выбранных из готовых процедур и функций) - 5-7 с,
10) разработка программы по схеме алгоритма - 1-2 с.
11) разработка инструкции пользования программой - 1 с.
12) распечатка программы (текстовый файл) – допускается привести как приложение – 2-3 страницы
13) распечатка исходных данных и результатов решения контрольного примера – 1-2 с.
14) заключение (подробные выводы по проделанной работе) – 1-2 с.
15) список использованной литературы – 1 с.
16) приложения (инструкции пользования программой и др.)
7. Графическая часть: алгоритм решения поставленной задачи – лист формата A1
8. Литература.
В рамках курсовой работы реализован словесный и на языке блок-схем алгоритм и программа на языке программирования Паскаль, которая вычисляет заданный интеграл по методы Гаусса и показывает графическое отображение процесса.
Объем работы – 23 листа, количество рисунков – 2, представлена одна программа.
Введение. 6
1. Анализ задания. 8
2. Выбор математической модели задачи. 10
2.1 Метод прямоугольников. 10
2.2 Метод парабол (метод Симпсона) 11
2.4 Увеличение точности. 11
2.5 Метод Гаусса. 12
2.6 Метод Гаусса-Кронрода. 12
3. Описание методов вычислительной математики, которые будут использованы при решении поставленной задачи. 14
3.1. Разработка алгоритма решения задачи и описание его особенностей 15
3.2 Разработка программы по схеме алгоритма. 18
3.3 Разработка инструкции пользования программой. 19
3.4 Распечатка программы.. 19
3.5 Распечатка исходных данных и результатов решения контрольного примера 26
Заключение. 27
Список использованной литературы.. 28
В настоящее время можно говорить, что появился новый способ теоретического исследования сложных процессов, допускающих математическое описание, - вычислительный эксперимент, т.е. исследование естественнонаучных проблем средствами вычислительной математики. Разработка и исследование вычислительных алгоритмов и их применение к решению конкретных задач составляет содержание огромного раздела современной математики - вычислительной математики.
Численные методы дают приближенное решение задачи. Это значит, что вместо точного решения и (функции или функционала) некоторой задачи мы находим решение у другой задачи, близкое в некотором смысле (например, по норме) к искомому. Основная идея всех методов - дискретизация или аппроксимация (замена, приближение) исходной задачи другой задачей, более удобной для решения на ЭВМ, причем решение аппроксимирующей задачи зависит от некоторых параметров, управляя которыми, можно определить решение с требуемой точностью. Например, в задаче численного интегрирования такими параметрами являются узлы и веса квадратурной формулы. Далее, решение дискретной задачи является элементом конечномерного пространства.
Численное интегрирование (историческое название: квадратура) - вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком интегрируемой функции и отрезками прямых, которые являются пределами интегрирования.
Необходимость применения численного интегрирования чаще всего может быть вызвана отсутствием у первообразной функции представления в элементарных функциях и, следовательно, невозможностью аналитического вычисления значения определённого интеграла по формуле Ньютона-Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом.

где 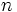 - число точек, в которых вычисляется значение подынтегральной функции. Точки
- число точек, в которых вычисляется значение подынтегральной функции. Точки 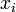 называются узлами метода, числа
называются узлами метода, числа  - весами узлов. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона). Часто формулы для оценки значения интеграла называют квадратурными формулами.
- весами узлов. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона). Часто формулы для оценки значения интеграла называют квадратурными формулами.
Пусть функция задана на интервале 
. Задача состоит в том, чтобы подобрать точки и коэффициенты так, чтобы квадратурная формула

(3.1)
была точной для всех полиномов наивысшей возможной степени.
Ввиду того, что имеется параметров и 
, а полином степени определяется коэффициентами, эта наивысшая степень в общем случае .
Таким образом, входными данными для нас будет являться подынтегральная функция f(x), пределы интегрирования a и b, количество узлов метода k. А также точность вычислений eps.
На выходе мы будем иметь значение определенного интеграла при заданном количестве разбиений и пределах интегрирования. Также мы получим графическое отображение процесса интегрирования на участках возрастания и убывания функции.
![\left[a, b\right]\,\!](https://bukvasha.net/img/28/dopb273046.zip) . Наиболее часто используются значения функции в середине отрезка и на его концах. Соответствующие модификации носят названия методов средних прямоугольников, левых прямоугольников и правых прямоугольников. Формула для приближенного вычисления значения определённого интеграла методом прямоугольников имеет вид
. Наиболее часто используются значения функции в середине отрезка и на его концах. Соответствующие модификации носят названия методов средних прямоугольников, левых прямоугольников и правых прямоугольников. Формула для приближенного вычисления значения определённого интеграла методом прямоугольников имеет вид
 ,
,
где 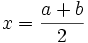 ,
,  или
или 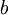 , соответственно.
, соответственно.
Метод трапеций
Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций.
Площадь трапеции на каждом отрезке: 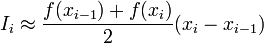 Погрешность аппроксимации на каждом отрезке:
Погрешность аппроксимации на каждом отрезке:  , где
, где ![M_{2,i}=\max_{x\mathcal{2}[x_{i-1},x_i]} \left| f''(x) \right|](https://bukvasha.net/img/28/dopb273053.zip) Полная формула трапеций в случае деления всего промежутка интегрирования на отрезки одинаковой длины h:
Полная формула трапеций в случае деления всего промежутка интегрирования на отрезки одинаковой длины h:  , где
, где 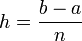 Погрешность формулы трапеций:
Погрешность формулы трапеций: 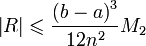 , где
, где ![M_{2}=\max_{x\mathcal{2}[a,b]} \left| f''(x) \right|](https://bukvasha.net/img/28/dopb273057.zip)
 .
.
Если разбить интервал интегрирования на 2N равных частей, то имеем
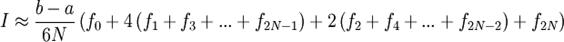 ,
,
где 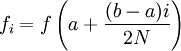 .
.
Для уменьшения погрешности отрезок интегрирования разбивают на части и применяют численный метод для оценки интеграла на каждой из них.
При стремлении количества разбиений к бесконечности, оценка интеграла стремится к его истинному значению для любого численного метода.
Приведённые выше методы допускают простую процедуру уменьшения шага в два раза, при этом на каждом шаге требуется вычислять значения функции только во вновь добавленных узлах. Для оценки погрешности вычислений используется правило Рунге.
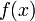 , то можно при том же количестве вычислений подынтегральной функции получить методы более высокого порядка точности. Так для двух (как в методе трапеций) вычислений значений подынтегральной функции, можно получить метод уже не 1-го, а 3-го порядка точности:
, то можно при том же количестве вычислений подынтегральной функции получить методы более высокого порядка точности. Так для двух (как в методе трапеций) вычислений значений подынтегральной функции, можно получить метод уже не 1-го, а 3-го порядка точности:
 .
.
В общем случае, используя 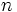 точек, можно получить метод с порядком точности
точек, можно получить метод с порядком точности 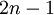 . Значения узлов метода Гаусса по
. Значения узлов метода Гаусса по 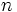 точкам являются корнями полинома Лежандра степени
точкам являются корнями полинома Лежандра степени 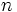 .
.
Значения узлов метода Гаусса и их весов приводятся в справочниках специальных функций. Наиболее известен метод Гаусса по пяти точкам.
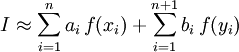 ,
,
где 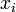 - узлы метода Гаусса по
- узлы метода Гаусса по 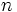 точкам, а
точкам, а  параметров
параметров  ,
,  ,
, 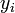 подобраны таким образом, чтобы порядок точности метода был равен
подобраны таким образом, чтобы порядок точности метода был равен  .
.
Тогда для оценки погрешности можно использовать эмпирическую формулу:
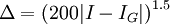 ,
,
где 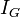 - приближённое значение интеграла, полученное методом Гаусса по
- приближённое значение интеграла, полученное методом Гаусса по  точкам.
точкам.
Аппроксимация, или приближение - математический метод, состоящий в замене одних математических объектов другими, в том или ином смысле близкими к исходным, но более простыми. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа.
Также в задачах такого рода активно используются интерполяционные методы нахождения значений функции.
Интерполя́ция - в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных экспериментальным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией кривой. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
На практике чаще всего применяют интерполяцию полиномами. Это связано прежде всего с тем, что полиномы легко вычислять, легко аналитически находить их производные и множество полиномов плотно в пространстве непрерывных функций.
(1.1)
была точной для всех полиномов наивысшей возможной степени.
Ввиду того, что имеется параметров и , а полином степени определяется коэффициентами, эта наивысшая степень в общем случае .
Запишем полином в виде и подставим в (1.1). Получим
,
.
Приравнивая выражения при одинаковых коэффициентах получим
, ,
, .
Итак, и находят из системы уравнений
,
,
, (1.2)
... ... .
.
Система (1.2) нелинейная, и ее решение найти довольно трудно. Рассмотрим еще один прием нахожденияи . Свойства полиномов Лежандра
,
таковы:
1) , ;
2) ;
3) полином Лежандра имеет различных и действительных корней, расположенных на интервале .
Составим по узлам интегрирования многочлен -й степени
.
Функция при есть многочлен степени не выше . Значит для этой функции формула Гаусса справедлива:
, (4.3)
так как .
Разложим в ряд по ортогональным многочленам Лежандра:
,
,
,
т.е. все коэффициенты при . Значит с точностью до численного множителя совпадает с . Таким образом, узлами формулы Гаусса являются нули многочлена Лежандра степени .
Зная , из линейной теперь системы первых (4.2) легко найти коэффициенты . Определитель этой системы есть определитель Вандермонда.
Формулу , в которой - нули полинома Лежандра , а определяют из (3.3), называют квадратурной формулой Гаусса.
Таким образом, алгоритм решения нашей задачи будет таким:
Ввод данных – пределы интегрирования, количество узлов, точность и подынтегральная функция
Подпрограмма вычисления интеграла с заданной точностью, которая использует подпрограмму вычисления функции десятиточечным методом
Подпрограмма графического отображения результатов вычислений по данному методу.
Подпрограммы реализованы в виде функций. Существует главная функция, которая вызывается из основной программы и которая выполняет основные действия (подсчет значения интеграла и вывод на экран результата, вывод графика на экран), вызывая другие подпрограммы.
Главная функция вызывает функцию подсчета интеграла с заданной точностью вычислений, которая в свою очередь на каждом шаге вызывает функцию подсчета значения функции.
После выбора нужного пункта в режиме диалога необходимо ввести соответствующие данные, результат появится на экране, а затем после нажатия клавиши ввода появится графическое отображение метода.
{ Вычисление интегpала десятиточечным методом Гаусса }
uses crt,graph;
var aaa,bbb,kkk: real;
{константы десятиточечного метода Гаусса}
const
g10c1=0.9739065285/6. 2012983932;
g10c2=0.8650633667/6. 2012983932;
g10c3=0.6794095683/6. 2012983932;
g10c4=0.4333953941/6. 2012983932;
g10c5=0.1488743390/6. 2012983932;
g10x1=0.0666713443/6. 2012983932;
g10x2=0.1494513492/6. 2012983932;
g10x3=0.2190863625/6. 2012983932;
g10x4=0.2692667193/6. 2012983932;
g10x5=0.2955242247/6. 2012983932;
function F(x: real): real; {интегрируемая функция}
begin
F: = kkk*(exp(-aaa*x) - exp(-bbb*x));
end;
function gauss_calc(a,b: real): real; {сам десятиточечный метод Гаусса}
var n,m,s,s1,s2,s3,s4,s5: real;
begin
m: =(b+a) /2; n: =(b-a) /2;
s1: =g10c1*(f(m+n*g10x1) +f(m-n*g10x1));
s2: =g10c2*(f(m+n*g10x2) +f(m-n*g10x2));
s3: =g10c3*(f(m+n*g10x3) +f(m-n*g10x3));
s4: =g10c4*(f(m+n*g10x4) +f(m-n*g10x4));
s5: =g10c5*(f(m+n*g10x5) +f(m-n*g10x5));
s: =s1+s2+s3+s4+s5;
gauss_calc: =s*(b-a);
end;
{рекурсивная ф-ция подсчета с заданной точностью}
{ gc - ранее посчитаный интеграл на интервале (a,b) }
function gauss(a,b,eps,gc: real): real;
var t,ga,gb: real;
begin
t: =(a+b) /2; {разбиваем интервал на две половинки}
ga: =gauss_calc(a,t); {в каждой половинке считаем интеграл}
gb: =gauss_calc(t,b);
if abs(ga+gb-gc) >eps then {проверяем точность вычислений}
begin
ga: =gauss(a,t,eps/2,ga); {рекурсия для первой половинки}
gb: =gauss(t,b,eps/2,gb); {рекурсия для второй половинки}
end; {при этом точность повышаем, чтобы }
{при сложении ошибка не накапливалась}
gauss: =ga+gb; {интеграл = сумме интегралов половинок}
end;
procedure inputnum(prm: string; var num: real; lb,ub: real); {процедура ввода данных}
var q: boolean;
begin
repeat
write('Введите ',prm,' '); readln(num);
q: =(lb>=num) or (num>ub);
if q then writeln('Число должно быть от ', lb: 0: 0,' до ',ub: 0: 0);
until not q;
end;
procedure titul; {Вывод титульного листа}
var f: text; s: string;
i: integer;
begin
clrscr;
assign(f,'f42. txt');
reset(f);
while not eof(f) do begin
readln(f,s);
while length(s) <79 do s: =' '+s+' ';
writeln(s);
end;
close(f);
end;
function main_menu: integer; {Главное меню}
var i: integer;
begin
Writeln('==========================================================');
Writeln('Что будем делать? ');
Writeln('----------------------------------------------------------');
Writeln('0 - выход');
Writeln('1 - решать тестовый пример a=1,5 b=6 k=10 eps = 0.0001');
Writeln('2 - решать пример с произвольными a, b, k, eps');
Writeln('----------------------------------------------------------');
Write('Выбор >>> '); readln(i);
Writeln('==========================================================');
main_menu: =i;
end;
procedure outputgraph(a,b,a1,b1: real; n: integer); {Вывод графика}
var i,j,j1,k: integer; t,y1,y2,x1,x2,x,y: double; s: string;
begin
clearviewport;
x1: =a1-1; x2: =b1+1;
if x1<0.5 then x1: =-0.5;
y2: =f(ln(bbb/aaa) /(bbb-aaa)) *1.2;
y1: =-y2;
{Линия y=0}
setcolor(15);
y: =0;
j: =trunc(480*(y-y2) /(y1-y2));
line(0,j,639,j);
{Линии x=a,x=b}
setcolor(5);
j: =trunc(480*(-y2) /(y1-y2));
i: =trunc(640*(a-x1) /(x2-x1));
j1: =trunc(480*(f(a) - y2) /(y1-y2));
line(i,j, i,j1);
i: =trunc(640*(b-x1) /(x2-x1));
j: =trunc(480*(-y2) /(y1-y2));
j1: =trunc(480*(f(b) - y2) /(y1-y2));
line(i,j, i,j1);
{Сам график}
setcolor(14);
setlinestyle(0,0,3);
t: =(b-a) /n;
k: =0;
j1: =trunc(480*(-y2) /(y1-y2));
for i: =0 to 640 do begin
x: =(x2-x1) *i/640+x1;
y: =f(x);
j: =trunc(480*(y-y2) /(y1-y2));
if j>479 then j: =479;
if j<0 then j: =0;
setcolor(14);
setlinestyle(0,0,3);
if i=0 then moveto(i,j) else lineto(i,j);
setcolor(8);
if (x>t*k+a) then begin
k: =k+1;
setcolor(15);
end;
setlinestyle(0,0,1);
if (x>=a) and (x<=b) then line(i,j, i,j1);
end;
setcolor(15);
y: =f(b);
i: =trunc(640*(b-x1) /(x2-x1));
j: =trunc(480*(y-y2) /(y1-y2));
line(i,j, i,j1);
setlinestyle(0,0,1);
setcolor(12);
{Подписи}
setcolor(13);
str(a: 6: 6,s);
s: ='a='+s;
i: =trunc(640*(a-x1) /(x2-x1));
outtextxy(i,j1+2,s);
str(b: 6: 6,s);
s: ='b='+s;
i: =trunc(640*(b-x1) /(x2-x1));
outtextxy(i-10,j1+2,s);
setcolor(15);
y: =0;
j: =trunc(480*(y-y2) /(y1-y2));
outtextxy(5,j+3,'y=0');
{Ждем... }
readkey;
end;
procedure equateit(a,b: real; eps: real); {процедура подсчета значения интеграла и вывода графика на экран}
var integral: real; i,j: integer;
begin
Integral: =gauss(a,b,eps,gauss_calc(a,b));
writeln('Интеграл = ', integral: 0: 6);
readkey;
i: =vga; j: =vgahi;
initgraph(i,j,'. . \bgi');
outputgraph(a,(b+a) /3,a,b,1);
outputgraph((b+a) /3,2*(b+a) /3,a,b,1);
outputgraph(2*(b+a) /3,b,a,b,1);
closegraph;
end;
var sel: integer;
eps: real;
begin
titul;
Writeln('==========================================================');
readkey;
repeat
clrscr;
sel: =main_menu;
case sel of
1: begin
aaa: =1.5; bbb: =6; kkk: =10;
eps: =1e-4;
equateit(aaa,bbb,eps);
end;
2: begin
inputnum('a',aaa,0,1000);
inputnum('b',bbb,-1000,1000);
inputnum('k',kkk,-1000,1000);
inputnum('точность',eps,0.000000001,1);
equateit(aaa,bbb,eps);
end;
end;
until sel=0;
end.


Представленный метод и реализованный алгоритм достаточно прост и эффективен для решения большого класса задач.
2. Немнюгин С.А. Turbo Pascal. – Спб.: Питер, 2002. – 496 с.
3. Фаронов В.В. Турбо Паскаль 7.0. Начальный курс. Учебное пособие. – М.: Нолидж, 1997. – 616 с.
4. Гусева А.И. Учимся программировать: PASCAL 7.0. Задачи и методы их решения. – М.: Диалог-МИФИ, 1997. – 256 с.
5. Дьяконов В.П. Справочник по алгоритмам и программам на языке бейсик для персональных ЭВМ: Справочник. - М.: Наука. Гл. ред. физ. -мат. лит., 1987. – 240 с.
6. Сапаров В.Е., Максимов Н.А. Системы стандартов в электросвязи и радиоэлектронике: Учебное пособие для вузов. – М. - Радио и связь, 1985. – 248 с.
7. ГОСТ 19.701-90 (ИСО 5807-85). “Единая система программной документации. Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения”/ Cб. ЕСПД. – М.: Изд-во стандартов, 1996. – 157 с.
8. Бахвалов Н., Жидков Н., Кобельков Г. Численные методы. М.: Лаборатория базовых знаний, 2001.632 с.
9. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений / Пер. с англ. М.: Мир, 1980.177с.
10. Самарский А.А., Гулин А.В. Численные методы: Учебное пособие для ВУЗов. М.: Наука, 1989.432с.
“Численное интегрирование методом Гаусса”
Федеральное агентство по образованию
Тульский государственный университет
КАФЕДРА РАДИОЭЛЕКТРОНИКИ
ИНФОРМАТИКА
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Вариант № 42
Студенту гр.220371 Подобеденко И.В.
1. Тема: "Численное интегрирование-методом Гаусса"
Разработайте алгоритм и программу:
1) вычисления определённого интеграла методом Гаусса и 2) построения графика функции я 3) построения нескольких (по 2 - 3) “шагов” интегрирования на участках возрастания и убывания функции.
Контрольный пример.
Исходные данные:
2. Срок представления курсовой работы на проверку с 12 по 15 мая 2008 г.
3. Защита курсовой работы с 19 по 23 мая 2008 г.
4. Требования к курсовой работе:
3.1 Разработать алгоритм и программу решения поставленной задачи.
3.2 Язык программирования - Паскаль.
3.3 Предусмотреть: а) диалоговый ввод исходных данных с проверкой правильности вводимых величин, б) блок пояснений к работе с программой, в) решение контрольного примера.
5. Форма отчётности:
пояснительная записка (ПЗ) объёмом 25-40 страниц на листах с рамками и штампом, отпечатанная на принтере,
графическая часть - лист формата А1,
дискета с текстом ПЗ, рисунком алгоритма и программой (текстовый и исполняемый файлы).
6. Содержание пояснительной записки к курсовой работе:
1) титульный лист,
2) задание на курсовую работу (настоявши бланк).
3) аннотация (краткая характеристика проделанной работы, объём ПЗ, количество таблиц, рисунков, схем. программ и приложений) с основной надписью по форме 2 (ГОСТ 2.104-68) - 1 с,
4) содержание (лист содержания и все последующие листы - с основной надписью по форме 2а - ГОСТ 2.104-68),
5) введение (область применения поставленной задачи, возможность использования ЭВМ для решения поставленной задачи) – 1-2 с,
6) анализ задания (выбор входных и выходных данных) – 2-3 с.
7) обзор литературных источников и разработка (выбор) математической модели задачи – 2-4 с,
8) описание методов вычислительной математики, которые будут использованы при решении поставленной задачи - 3-4 с,
9) разработка алгоритма решения задачи и описание его особенностей (разработанных или выбранных из готовых процедур и функций) - 5-7 с,
10) разработка программы по схеме алгоритма - 1-2 с.
11) разработка инструкции пользования программой - 1 с.
12) распечатка программы (текстовый файл) – допускается привести как приложение – 2-3 страницы
13) распечатка исходных данных и результатов решения контрольного примера – 1-2 с.
14) заключение (подробные выводы по проделанной работе) – 1-2 с.
15) список использованной литературы – 1 с.
16) приложения (инструкции пользования программой и др.)
7. Графическая часть: алгоритм решения поставленной задачи – лист формата A1
8. Литература.
Аннотация
В работе рассмотрены методы численного интегрирования функций. Для подробного рассмотрения был взят метод Гаусса.В рамках курсовой работы реализован словесный и на языке блок-схем алгоритм и программа на языке программирования Паскаль, которая вычисляет заданный интеграл по методы Гаусса и показывает графическое отображение процесса.
Объем работы – 23 листа, количество рисунков – 2, представлена одна программа.
Содержание
Аннотация. 4Введение. 6
1. Анализ задания. 8
2. Выбор математической модели задачи. 10
2.1 Метод прямоугольников. 10
2.2 Метод парабол (метод Симпсона) 11
2.4 Увеличение точности. 11
2.5 Метод Гаусса. 12
2.6 Метод Гаусса-Кронрода. 12
3. Описание методов вычислительной математики, которые будут использованы при решении поставленной задачи. 14
3.1. Разработка алгоритма решения задачи и описание его особенностей 15
3.2 Разработка программы по схеме алгоритма. 18
3.3 Разработка инструкции пользования программой. 19
3.4 Распечатка программы.. 19
3.5 Распечатка исходных данных и результатов решения контрольного примера 26
Заключение. 27
Список использованной литературы.. 28
Введение
Появление и непрерывное совершенствование быстродействующих электронных вычислительных машин (ЭВМ) привело к подлинно революционному преобразованию пауки вообще и математики в особенности. Изменилась технология научных исследований, колоссально увеличились возможности теоретического изучения, прогноза сложных процессов, проектирования инженерных конструкций. Решение крупных научно-технических проблем, примерами которых могут служить проблемы овладения ядерной энергией и освоения космоса, стало возможным лишь благодаря применению математического моделирования и новых численных методов, предназначенных для ЭВМ.В настоящее время можно говорить, что появился новый способ теоретического исследования сложных процессов, допускающих математическое описание, - вычислительный эксперимент, т.е. исследование естественнонаучных проблем средствами вычислительной математики. Разработка и исследование вычислительных алгоритмов и их применение к решению конкретных задач составляет содержание огромного раздела современной математики - вычислительной математики.
Численные методы дают приближенное решение задачи. Это значит, что вместо точного решения и (функции или функционала) некоторой задачи мы находим решение у другой задачи, близкое в некотором смысле (например, по норме) к искомому. Основная идея всех методов - дискретизация или аппроксимация (замена, приближение) исходной задачи другой задачей, более удобной для решения на ЭВМ, причем решение аппроксимирующей задачи зависит от некоторых параметров, управляя которыми, можно определить решение с требуемой точностью. Например, в задаче численного интегрирования такими параметрами являются узлы и веса квадратурной формулы. Далее, решение дискретной задачи является элементом конечномерного пространства.
Численное интегрирование (историческое название: квадратура) - вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком интегрируемой функции и отрезками прямых, которые являются пределами интегрирования.
Необходимость применения численного интегрирования чаще всего может быть вызвана отсутствием у первообразной функции представления в элементарных функциях и, следовательно, невозможностью аналитического вычисления значения определённого интеграла по формуле Ньютона-Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом.
1. Анализ задания
Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При этом для оценки значения интеграла получаются формулы видагде
Пусть функция задана на интервале

была точной для всех полиномов наивысшей возможной степени.
Ввиду того, что имеется параметров и
Таким образом, входными данными для нас будет являться подынтегральная функция f(x), пределы интегрирования a и b, количество узлов метода k. А также точность вычислений eps.
На выходе мы будем иметь значение определенного интеграла при заданном количестве разбиений и пределах интегрирования. Также мы получим графическое отображение процесса интегрирования на участках возрастания и убывания функции.
2. Выбор математической модели задачи
Кратко рассмотрим основные методы численного интегрирования и выясним почему метод Гаусса наиболее подходит для решения нашей задачи.2.1 Метод прямоугольников
Метод прямоугольников получается при замене подынтегральной функции на константу. В качестве константы можно взять значение функции в любой точке отрезкагде
Метод трапеций
Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций.
Площадь трапеции на каждом отрезке:
 , где
, где 2.2 Метод парабол (метод Симпсона)
Использовав три точки отрезка интегрирования можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид .
. Если разбить интервал интегрирования на 2N равных частей, то имеем
где
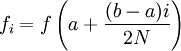 .
. 2.4 Увеличение точности
Приближение функции одним полиномом на всем отрезке интегрирования, как правило, приводит к большой ошибке в оценке значения интеграла.Для уменьшения погрешности отрезок интегрирования разбивают на части и применяют численный метод для оценки интеграла на каждой из них.
При стремлении количества разбиений к бесконечности, оценка интеграла стремится к его истинному значению для любого численного метода.
Приведённые выше методы допускают простую процедуру уменьшения шага в два раза, при этом на каждом шаге требуется вычислять значения функции только во вновь добавленных узлах. Для оценки погрешности вычислений используется правило Рунге.
2.5 Метод Гаусса
Описанные выше методы используют фиксированные точки отрезка (концы и середину) и имеют низкий порядок точности (0 - методы правых и левых прямоугольников, 1 - методы средних прямоугольников и трапеций, 3 - метод парабол (Симпсона)). Если мы можем выбирать точки, в которых мы вычисляем значения функции .
. В общем случае, используя
Значения узлов метода Гаусса и их весов приводятся в справочниках специальных функций. Наиболее известен метод Гаусса по пяти точкам.
2.6 Метод Гаусса-Кронрода
Недостаток метода Гаусса состоит в том, что он не имеет лёгкого (с вычислительной точки зрения) пути оценки погрешности полученного значения интеграла. Использование правила Рунге требует вычисления подынтегральной функции примерно в таком же числе точек, не давая при этом практически никакого выигрыша точности, в отличие от простых методов, где точность увеличивается в разы при каждом новом разбиении. Кронродом был предложен следующий метод оценки значения интеграла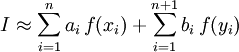 ,
,где
Тогда для оценки погрешности можно использовать эмпирическую формулу:
где
3. Описание методов вычислительной математики, которые будут использованы при решении поставленной задачи
Сущность большинства методов вычисления определенных интегралов состоит в заменен подынтегральной функции апроксимирующей функцией, для которой можно легко записать первообразную в элементарных функциях.Аппроксимация, или приближение - математический метод, состоящий в замене одних математических объектов другими, в том или ином смысле близкими к исходным, но более простыми. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа.
Также в задачах такого рода активно используются интерполяционные методы нахождения значений функции.
Интерполя́ция - в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных экспериментальным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией кривой. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
На практике чаще всего применяют интерполяцию полиномами. Это связано прежде всего с тем, что полиномы легко вычислять, легко аналитически находить их производные и множество полиномов плотно в пространстве непрерывных функций.
3.1. Разработка алгоритма решения задачи и описание его особенностей
Пусть функция задана на стандартном интервале . Задача состоит в том, чтобы подобрать точки и коэффициенты так, чтобы квадратурная формула(1.1)
была точной для всех полиномов наивысшей возможной степени.
Ввиду того, что имеется параметров и , а полином степени определяется коэффициентами, эта наивысшая степень в общем случае .
Запишем полином в виде и подставим в (1.1). Получим
,
.
Приравнивая выражения при одинаковых коэффициентах получим
, ,
, .
Итак, и находят из системы уравнений
,
,
, (1.2)
... ... .
.
Система (1.2) нелинейная, и ее решение найти довольно трудно. Рассмотрим еще один прием нахожденияи . Свойства полиномов Лежандра
,
таковы:
1) , ;
2) ;
3) полином Лежандра имеет различных и действительных корней, расположенных на интервале .
Составим по узлам интегрирования многочлен -й степени
.
Функция при есть многочлен степени не выше . Значит для этой функции формула Гаусса справедлива:
, (4.3)
так как .
Разложим в ряд по ортогональным многочленам Лежандра:
,
,
,
т.е. все коэффициенты при . Значит с точностью до численного множителя совпадает с . Таким образом, узлами формулы Гаусса являются нули многочлена Лежандра степени .
Зная , из линейной теперь системы первых (4.2) легко найти коэффициенты . Определитель этой системы есть определитель Вандермонда.
Формулу , в которой - нули полинома Лежандра , а определяют из (3.3), называют квадратурной формулой Гаусса.
Таким образом, алгоритм решения нашей задачи будет таким:
Ввод данных – пределы интегрирования, количество узлов, точность и подынтегральная функция
Подпрограмма вычисления интеграла с заданной точностью, которая использует подпрограмму вычисления функции десятиточечным методом
Подпрограмма графического отображения результатов вычислений по данному методу.
3.2 Разработка программы по схеме алгоритма
В основной программе необходимо предусмотреть ввод необходимых данных и реализацию контрольно примера, а также удобное управление элементами программы и команду выхода.Подпрограммы реализованы в виде функций. Существует главная функция, которая вызывается из основной программы и которая выполняет основные действия (подсчет значения интеграла и вывод на экран результата, вывод графика на экран), вызывая другие подпрограммы.
Главная функция вызывает функцию подсчета интеграла с заданной точностью вычислений, которая в свою очередь на каждом шаге вызывает функцию подсчета значения функции.
3.3 Разработка инструкции пользования программой
Программный комплекс имеет интуитивно понятный интерфейс. Вначале программы на экран выводится меню, где можно выбрать несколько дальнейших действий, а именно: решение контрольного примера, произвольный ввод данных или выход из программы.После выбора нужного пункта в режиме диалога необходимо ввести соответствующие данные, результат появится на экране, а затем после нажатия клавиши ввода появится графическое отображение метода.
3.4 Распечатка программы
{$N+}{ Вычисление интегpала десятиточечным методом Гаусса }
uses crt,graph;
var aaa,bbb,kkk: real;
{константы десятиточечного метода Гаусса}
const
g10c1=0.9739065285/6. 2012983932;
g10c2=0.8650633667/6. 2012983932;
g10c3=0.6794095683/6. 2012983932;
g10c4=0.4333953941/6. 2012983932;
g10c5=0.1488743390/6. 2012983932;
g10x1=0.0666713443/6. 2012983932;
g10x2=0.1494513492/6. 2012983932;
g10x3=0.2190863625/6. 2012983932;
g10x4=0.2692667193/6. 2012983932;
g10x5=0.2955242247/6. 2012983932;
function F(x: real): real; {интегрируемая функция}
begin
F: = kkk*(exp(-aaa*x) - exp(-bbb*x));
end;
function gauss_calc(a,b: real): real; {сам десятиточечный метод Гаусса}
var n,m,s,s1,s2,s3,s4,s5: real;
begin
m: =(b+a) /2; n: =(b-a) /2;
s1: =g10c1*(f(m+n*g10x1) +f(m-n*g10x1));
s2: =g10c2*(f(m+n*g10x2) +f(m-n*g10x2));
s3: =g10c3*(f(m+n*g10x3) +f(m-n*g10x3));
s4: =g10c4*(f(m+n*g10x4) +f(m-n*g10x4));
s5: =g10c5*(f(m+n*g10x5) +f(m-n*g10x5));
s: =s1+s2+s3+s4+s5;
gauss_calc: =s*(b-a);
end;
{рекурсивная ф-ция подсчета с заданной точностью}
{ gc - ранее посчитаный интеграл на интервале (a,b) }
function gauss(a,b,eps,gc: real): real;
var t,ga,gb: real;
begin
t: =(a+b) /2; {разбиваем интервал на две половинки}
ga: =gauss_calc(a,t); {в каждой половинке считаем интеграл}
gb: =gauss_calc(t,b);
if abs(ga+gb-gc) >eps then {проверяем точность вычислений}
begin
ga: =gauss(a,t,eps/2,ga); {рекурсия для первой половинки}
gb: =gauss(t,b,eps/2,gb); {рекурсия для второй половинки}
end; {при этом точность повышаем, чтобы }
{при сложении ошибка не накапливалась}
gauss: =ga+gb; {интеграл = сумме интегралов половинок}
end;
procedure inputnum(prm: string; var num: real; lb,ub: real); {процедура ввода данных}
var q: boolean;
begin
repeat
write('Введите ',prm,' '); readln(num);
q: =(lb>=num) or (num>ub);
if q then writeln('Число должно быть от ', lb: 0: 0,' до ',ub: 0: 0);
until not q;
end;
procedure titul; {Вывод титульного листа}
var f: text; s: string;
i: integer;
begin
clrscr;
assign(f,'f42. txt');
reset(f);
while not eof(f) do begin
readln(f,s);
while length(s) <79 do s: =' '+s+' ';
writeln(s);
end;
close(f);
end;
function main_menu: integer; {Главное меню}
var i: integer;
begin
Writeln('==========================================================');
Writeln('Что будем делать? ');
Writeln('----------------------------------------------------------');
Writeln('0 - выход');
Writeln('1 - решать тестовый пример a=1,5 b=6 k=10 eps = 0.0001');
Writeln('2 - решать пример с произвольными a, b, k, eps');
Writeln('----------------------------------------------------------');
Write('Выбор >>> '); readln(i);
Writeln('==========================================================');
main_menu: =i;
end;
procedure outputgraph(a,b,a1,b1: real; n: integer); {Вывод графика}
var i,j,j1,k: integer; t,y1,y2,x1,x2,x,y: double; s: string;
begin
clearviewport;
x1: =a1-1; x2: =b1+1;
if x1<0.5 then x1: =-0.5;
y2: =f(ln(bbb/aaa) /(bbb-aaa)) *1.2;
y1: =-y2;
{Линия y=0}
setcolor(15);
y: =0;
j: =trunc(480*(y-y2) /(y1-y2));
line(0,j,639,j);
{Линии x=a,x=b}
setcolor(5);
j: =trunc(480*(-y2) /(y1-y2));
i: =trunc(640*(a-x1) /(x2-x1));
j1: =trunc(480*(f(a) - y2) /(y1-y2));
line(i,j, i,j1);
i: =trunc(640*(b-x1) /(x2-x1));
j: =trunc(480*(-y2) /(y1-y2));
j1: =trunc(480*(f(b) - y2) /(y1-y2));
line(i,j, i,j1);
{Сам график}
setcolor(14);
setlinestyle(0,0,3);
t: =(b-a) /n;
k: =0;
j1: =trunc(480*(-y2) /(y1-y2));
for i: =0 to 640 do begin
x: =(x2-x1) *i/640+x1;
y: =f(x);
j: =trunc(480*(y-y2) /(y1-y2));
if j>479 then j: =479;
if j<0 then j: =0;
setcolor(14);
setlinestyle(0,0,3);
if i=0 then moveto(i,j) else lineto(i,j);
setcolor(8);
if (x>t*k+a) then begin
k: =k+1;
setcolor(15);
end;
setlinestyle(0,0,1);
if (x>=a) and (x<=b) then line(i,j, i,j1);
end;
setcolor(15);
y: =f(b);
i: =trunc(640*(b-x1) /(x2-x1));
j: =trunc(480*(y-y2) /(y1-y2));
line(i,j, i,j1);
setlinestyle(0,0,1);
setcolor(12);
{Подписи}
setcolor(13);
str(a: 6: 6,s);
s: ='a='+s;
i: =trunc(640*(a-x1) /(x2-x1));
outtextxy(i,j1+2,s);
str(b: 6: 6,s);
s: ='b='+s;
i: =trunc(640*(b-x1) /(x2-x1));
outtextxy(i-10,j1+2,s);
setcolor(15);
y: =0;
j: =trunc(480*(y-y2) /(y1-y2));
outtextxy(5,j+3,'y=0');
{Ждем... }
readkey;
end;
procedure equateit(a,b: real; eps: real); {процедура подсчета значения интеграла и вывода графика на экран}
var integral: real; i,j: integer;
begin
Integral: =gauss(a,b,eps,gauss_calc(a,b));
writeln('Интеграл = ', integral: 0: 6);
readkey;
i: =vga; j: =vgahi;
initgraph(i,j,'. . \bgi');
outputgraph(a,(b+a) /3,a,b,1);
outputgraph((b+a) /3,2*(b+a) /3,a,b,1);
outputgraph(2*(b+a) /3,b,a,b,1);
closegraph;
end;
var sel: integer;
eps: real;
begin
titul;
Writeln('==========================================================');
readkey;
repeat
clrscr;
sel: =main_menu;
case sel of
1: begin
aaa: =1.5; bbb: =6; kkk: =10;
eps: =1e-4;
equateit(aaa,bbb,eps);
end;
2: begin
inputnum('a',aaa,0,1000);
inputnum('b',bbb,-1000,1000);
inputnum('k',kkk,-1000,1000);
inputnum('точность',eps,0.000000001,1);
equateit(aaa,bbb,eps);
end;
end;
until sel=0;
end.
3.5 Распечатка исходных данных и результатов решения контрольного примера


Заключение
В данной работе описана и реализована с помощью блок-схем и языка программирования Turbo Pascal задача нахождения численного решения интеграла методом Гаусса. Программное средство содержит средства вычисления интеграла по исходным данным, а также выбирая произвольный интервал и шаг интегрирования с заданной точностью. При этом на экран выводится график, отражающий процесс интегрирования заданной функции по шагам.Представленный метод и реализованный алгоритм достаточно прост и эффективен для решения большого класса задач.
Список использованной литературы
1. Малыхина М.П. Программирование на языке высокого уровня Turbo Pascal. – Спб.: БХВ-Петербург, 2006, 544 с.2. Немнюгин С.А. Turbo Pascal. – Спб.: Питер, 2002. – 496 с.
3. Фаронов В.В. Турбо Паскаль 7.0. Начальный курс. Учебное пособие. – М.: Нолидж, 1997. – 616 с.
4. Гусева А.И. Учимся программировать: PASCAL 7.0. Задачи и методы их решения. – М.: Диалог-МИФИ, 1997. – 256 с.
5. Дьяконов В.П. Справочник по алгоритмам и программам на языке бейсик для персональных ЭВМ: Справочник. - М.: Наука. Гл. ред. физ. -мат. лит., 1987. – 240 с.
6. Сапаров В.Е., Максимов Н.А. Системы стандартов в электросвязи и радиоэлектронике: Учебное пособие для вузов. – М. - Радио и связь, 1985. – 248 с.
7. ГОСТ 19.701-90 (ИСО 5807-85). “Единая система программной документации. Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения”/ Cб. ЕСПД. – М.: Изд-во стандартов, 1996. – 157 с.
8. Бахвалов Н., Жидков Н., Кобельков Г. Численные методы. М.: Лаборатория базовых знаний, 2001.632 с.
9. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений / Пер. с англ. М.: Мир, 1980.177с.
10. Самарский А.А., Гулин А.В. Численные методы: Учебное пособие для ВУЗов. М.: Наука, 1989.432с.