Лабораторная работа на тему Графы Основные понятия
Работа добавлена на сайт bukvasha.net: 2014-12-15Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Министерство образования и науки Российской Федерации
Курский государственный технический университет
Кафедра ПО ВТ и АС
Лабораторная работа № 1
Графы. Основные понятия
Выполнил: студент гр. ПО 62 Шиляков И.А.
Проверил: доцентТомакова Р.А.
Курск 2007
Задание:
1. По заданным матрицам смежности вершин восстановить графы.
2. Построить для каждого графа матрицу смежности ребер, инцидентности, достижимости, контрдостижимости.
3. Найти и построить объединение, пересечение, кольцевую сумму заданных графов.
4. Найти композицию графов 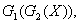
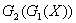
.
5. Для каждого графа найти и построить остовный подграф, произвольный подграф, порожденный подграф.
6. Определить локальные степени вершин графа, проверить существует ли в данном графе эйлерова цепь, эйлеров цикл.
7. Определить хроматические и цикломатические числа данных графов.
8. Найти все базы графа.
9. Определить в каждом графе сильные компоненты связности, построить конденсацию графа.
Выполнение:
1. По заданным матрицам смежности вершин восстановить графы.
A1
SHAPE \* MERGEFORMAT

G1(X1,A1)
A2
SHAPE \* MERGEFORMAT

G2(X2,A2)
2. Построить для каждого графа матрицу смежности ребер, инцидентности, достижимости, контрдостижимости.
B1
B2
S1
S2
R1 R2
Курский государственный технический университет
Кафедра ПО ВТ и АС
Лабораторная работа № 1
Графы. Основные понятия
Выполнил: студент гр. ПО 62 Шиляков И.А.
Проверил: доцентТомакова Р.А.
Курск 2007
Задание:
1. По заданным матрицам смежности вершин восстановить графы.
2. Построить для каждого графа матрицу смежности ребер, инцидентности, достижимости, контрдостижимости.
3. Найти и построить объединение, пересечение, кольцевую сумму заданных графов.
4. Найти композицию графов
5. Для каждого графа найти и построить остовный подграф, произвольный подграф, порожденный подграф.
6. Определить локальные степени вершин графа, проверить существует ли в данном графе эйлерова цепь, эйлеров цикл.
7. Определить хроматические и цикломатические числа данных графов.
8. Найти все базы графа.
9. Определить в каждом графе сильные компоненты связности, построить конденсацию графа.
Выполнение:
1. По заданным матрицам смежности вершин восстановить графы.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| x1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| x2 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| x3 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| x4 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| x5 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| x6 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| x7 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
|
| X1 |
| X3 |
| X4 |
| X6 |
| X7 |
| X5 |
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
| a6 |
| a7 |
| a8 |
| a9 |
| a10 |
| a11 |
| a12 |
| a13 |
| a14 |

G1(X1,A1)
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| x1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| x2 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| x3 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| x4 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| x5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| x6 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| x7 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
|
| X3 |
| X4 |
| X5 |
| X6 |
| X7 |
| X1 |
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
| a6 |
| a7 |
| a8 |
| a9 |
| a10 |
| a11 |
| a12 |
| a14 |
| a13 |

G2(X2,A2)
2. Построить для каждого графа матрицу смежности ребер, инцидентности, достижимости, контрдостижимости.
| а1 | а2 | а3 | а4 | а5 | а6 | а7 | а8 | а9 | а10 | а11 | а12 | а13 | а14 | |
| а1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| а2 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| а3 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| а4 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| а5 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| а6 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| а7 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| а8 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| а9 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| а10 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| а11 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| а12 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| а13 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| а14 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| а1 | а2 | а3 | а4 | а5 | а6 | а7 | а8 | а9 | а10 | а11 | а12 | а13 | а14 | |
| а1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| а2 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| а3 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| а4 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| а5 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| а6 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| а7 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| а8 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| а9 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| а10 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| а11 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| а12 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| а13 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| а14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| а1 | а2 | а3 | а4 | а5 | а6 | а7 | а8 | а9 | а10 | а11 | а12 | а13 | а14 | |
| x1 | 1 | 1 | 0 | 0 | 0 | 0 | -1 | 0 | -1 | 0 | 0 | 0 | 0 | 0 |
| x2 | -1 | 0 | 1 | 1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| x3 | 0 | 0 | -1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 |
| x4 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 1 | 0 | 0 | 0 | -1 | 0 | 0 |
| x5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 1 | 0 | 0 | -1 | 0 |
| x6 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | -1 |
| x7 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 1 | 1 |
| а1 | а2 | а3 | а4 | а5 | а6 | а7 | а8 | а9 | а10 | а11 | а12 | а13 | а14 | |
| x1 | 1 | 0 | 0 | 1 | 0 | 0 | -1 | 0 | -1 | 0 | 0 | 0 | 0 | 0 |
| x2 | 0 | -1 | 1 | -1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| x3 | -1 | 1 | 0 | 0 | -1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| x4 | 0 | 0 | -1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | -1 | 1 | 0 |
| x5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 1 | 0 | -1 | 1 |
| x6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | -1 | 0 | 1 | 0 | -1 |
| x7 | 0 | 0 | 0 | 0 | 1 | -1 | 0 | 0 | 0 | 1 | -1 | 0 | 0 | 0 |
S2
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| x1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| x1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| x1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| x1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Q1 Q2
3. Найти и построить объединение, пересечение, кольцевую сумму заданных графов.
Объединение графов
SHAPE \* MERGEFORMAT
| X1 |
| X3 |
| X4 |
| X6 |
| X7 |
| X5 |
| X2 |

G3(X3,A3)=G1(X1,A1) YG2(X2,A2); X3= X1YX2, A3= A1YA2
Пересечение графов
SHAPE \* MERGEFORMAT
| X1 |
| X3 |
| X4 |
| X6 |
| X7 |
| X5 |
| X2 |

G3(X3,A3)=G1(X1,A1) ∩G2(X2,A2); X3= X1∩X2, A3= A1∩A2
Кольцевая сумма графов
SHAPE \* MERGEFORMAT
| X1 |
| X3 |
| X4 |
| X6 |
| X7 |
| X5 |
| X2 |

G3(X3,A3)=G1(X1,A1)
4. Найти и построить композицию графов
| G1(Х) | G2(Х) | G1(G2(Х)) | G2(G1(Х)) | |
| x1 | (x1,x2), (x1,x7) | (x1,x2), (x1,x3) | (x1,x3), (x1,x6), (x1,x2), (x1,x4), | (x1,x4), (x1,x5), (x1,x3), (x1,x6), |
| x2 | (x2,x3), (x2,x6) | (x2,x4), (x2,x5) | (x2,x1), (x2,x5), (x2,x7), | (x2,x2), (x2,x7), (x2,x1), (x2,x4), |
| x3 | (x3,x2), (x3,x4) | (x3,x2), (x3,x7) | (x3,x3), (x3,x6), (x3,x5), | (x3,x4), (x3,x5), (x3,x1), |
| x4 | (x4,x1), (x4,x5) | (x4,x1), (x4,x5) | (x4,x2), (x4,x7), (x4,x1), | (x4,x2), (x4,x3), (x4,x6), (x4,x7), |
| x5 | (x5,x1), (x5,x7) | (x5,x6), (x5,x7) | (x5,x3), (x5,x4), (x5,x5), (x5,x6), | (x5,x2), (x5,x3), (x5,x6), |
| x6 | (x6,x3), (x6,x4) | (x6,x1), (x6,x4) | (x6,x2), (x6,x7), (x6,x1), (x6,x5), | (x6,x2), (x6,x7), (x6,x1), (x6,x5), |
| x7 | (x7,x5), (x7,x6) | (x7,x3), (x7,x6) | (x7,x2), (x7,x4), (x7,x3), | (x7,x6), (x7,x7), (x7,x1), (x7,x4), |
| X1 |
| X3 |
| X4 |
| X6 |
| X7 |
| X5 |
| X2 |

SHAPE \* MERGEFORMAT
| X1 |
| X3 |
| X4 |
| X7 |
| X5 |
| X2 |
| X6 |

G2(G1(Х))
5. Для каждого графа найти и построить остовный подграф, произвольный подграф, порожденный подграф.
Остовные подграфы
SHAPE \* MERGEFORMAT
| X1 |
| X3 |
| X4 |
| X6 |
| X7 |
| X5 |
| a1 |
| a3 |
| a6 |
| a9 |
| a12 |
| a13 |
| a14 |
| X2 |

G’1(X1,A1)
SHAPE \* MERGEFORMAT
| X3 |
| X4 |
| X5 |
| X6 |
| X7 |
| X1 |
| a1 |
| a2 |
| a3 |
| a9 |
| a10 |
| a14 |
| a13 |
| X2 |

G’2(X2,A2)
Произвольные подграфы
SHAPE \* MERGEFORMAT
| X1 |
| X3 |
| X4 |
| X6 |
| a1 |
| a3 |
| a6 |
| a12 |

G1’’ (X1’’,A1’’)
SHAPE \* MERGEFORMAT
| X3 |
| X4 |
| X1 |
| a1 |
| a2 |
| a3 |

|
Порожденные подграфы
|
| X1 |
| X7 |
| X5 |
| a2 |
| a9 |
| a13 |
| a1 |
| a10 |
| X6 |
| a6 |
| a9 |

G1P(X1P,A1P) G2P(X2P,A2P)
6. Определить локальные степени вершин графа, проверить существует ли в данном графе эйлерова цепь, эйлеров цикл.
Локальные степени графа G1
Локальные степени графа G2
Эйлерова цепь существует в двух графах, т.к. все локальные степени графов четны.
Эйлеров цикл существует в двух графах, т.к. все локальные степени графов четны.
7. Определить хроматические и цикломатические числа данных графов.
SHAPE \* MERGEFORMAT
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
| X1 |
| X3 |
| X6 |
| X7 |
| X5 |
| X2 |
| X4 |

Хроматическое число γ для графа G1 = 4
SHAPE \* MERGEFORMAT
| 3 |
| 1 |
| 2 |
| 4 |
| 1 |
| 2 |
| 3 |
| X3 |
| X6 |
| X7 |
| X1 |
| X2 |
| X4 |
| X5 |

Хроматическое число γ для графа G2 = 4
Цикломатические числа графов
V(G1)=m-n+r, где m - число рёбер (дуг);
n – число вершин;
r – число компонент связности.
V(G1)=14-7+1=8;
V(G2)=14-7+1=8;
8. Найти все базы графа.
Базы графа G1
B1={x1}
B2={x2}
B3={x3}
B4={x4}
B5={x5}
B6={x6}
B7={x7}
Базы графа G2
B1={x1}
B2={x2}
B3={x3}
B4={x4}
B5={x5}
B6={x6}
B7={x7}
B1={x1}
B2={x2}
B3={x3}
B4={x4}
B5={x5}
B6={x6}
B7={x7}
Базы графа G2
B1={x1}
B2={x2}
B3={x3}
B4={x4}
B5={x5}
B6={x6}
B7={x7}
9. Определить в каждом графе сильные компоненты связности, построить конденсацию графа.
Сильные компоненты связности G1
СК={x1, x2, x3, x4, x5, x6, x7}
Сильные компоненты связности G2
СК={x1, x2, x3, x4, x5, x6, x7}
SHAPE \* MERGEFORMAT

SHAPE \* MERGEFORMAT

Конденсация графа G1 Конденсация графа G2
Сильные компоненты связности G1
СК={x1, x2, x3, x4, x5, x6, x7}
Сильные компоненты связности G2
СК={x1, x2, x3, x4, x5, x6, x7}
SHAPE \* MERGEFORMAT
| |
| Z1 |

| |
| Z1 |

Конденсация графа G1 Конденсация графа G2