канд. биол. наук М.П.Иванов, д-р техн. наук В.В.Кашинов

ФНИИ им.А.А.Ухтомского, СПбГУ

Во многихсистемах, например, спутниковой навигационной системе GPS NAVSTAR, асинхронных адресныхсистемахсвязи (ААСС) и т.д. используются сигналы, излучаемые многими источниками на одной несущей частоте и адресованные разным потребителям. При этом для приема используется согласованная с тем сигналом, который нужно принять, фильтрация или корреляционный прием. Возможно, применение частотно-временной фильтрации [1]. В таких системах неизбежно появление перекрестных внутрисистемных помех, которые желательно минимизировать. В работе [2] показано, что при определении качества системы по среднему интегральному эффекту взаимных помех непрерывные сигналы должны иметь одинаковые автокорреляционные функции, то есть должны различаться только фазовыми характеристиками. Этот критерий целесообразно использовать, если взаимные корреляционные функции (ВКФ) имеют один значительный всплеск Rkm, которым,восновном,иопределяется критерий - величина, или, наоборот, имеют много всплесков одного порядка. Однако в упомянутой работе [2] не приведена процедура построения самой системы сигналов.

Примем за критерий оптимальности максимальную величину всплесков ВКФ, а сигналы оптимальной системы определим в классе функций, связанных между собой линейными операторами. Все реальные сигналы принадлежат энергетическому пространству L2, а общий вид линейного оператора, действующего из L2 в L2, - интегральный, поэтому искомая система сигналов является единственной.

Обозначим как искомую систему сигналов, построеннуюна базе некоторого основного (условного) сигнала S0 по правилу

 (1)

где Ak - линейный интегральный оператор с ядром hk (u):

 (2)

Будем считать основной сигнал S0 реализацией некоторого случайного стационарного процесса с интервалом корреляции tcor << T, получим для ВКФ Rkm k-го и m-го сигналов

 (3)

В частности, как известно [3],

 (4)

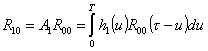
и

 (5)

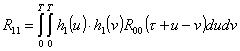
Экстремальные значения ВКФ всех сигналов Sk достигаются в моментывремени относительномаксимумаосновногосигналаx0, которые определяются уравнениями

 (6)

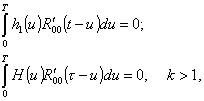
где H(u) - ядро произведения линейных интегральных операторов Ak Ak-1 -A1.

Чтобы исключить тривиальные решения Ak º 0, введем естественные ограничения на энергию функций hk(u):

 (7)

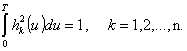
Тогда первая вариация функционала R10 с учетом ограничений (6) и (7) будет иметь вид

 (8)

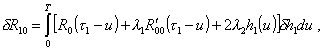
где l1 и l2 - неопределенные пока множители Лагранжа.

Используя результаты работы [4], получим обобщенное уравнение Эйлера-Пуассона для функции h1(u), доставляющей экстремум функционалу R10

 (9)

Множитель Лагранжа l2 находится при интегрировании по интервалу T обеих частей уравнения (9), умноженных на ядро h1(u), а множитель l1 - путем подобного интегрирования после возведения обеих частей уравнения в квадрат. Выполняя преобразования с учетом ограничений (6) и (7) и формулы (5), получим для ядра оператора A1, определяющего первый сигнал системы S1, и для корреляционной функции этого сигнала следующие выражения

 (10)

где коэффициент a1 является корнем квадратного уравнения

 (11)

Подходящая экстремаль h1(u) формулы (10) обуславливает величину перекрестной помехи P10 обнаружителя сигнала S1 при наличии основного сигнала S0

 (12)

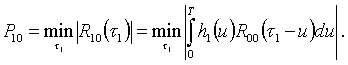
Аналогично могут быть найдены оптимальные в сформулированном смысле ядра операторов A2, A3, - и соответствующие перекрестные помехи P20, P30, ... и P31, P42, ... и т.д.

Расширение системы сигналов ограничивается величиной допустимых перекрестных помех.

Заметим, что принятая процедура установления последовательности линейных интегральных операторов A1, A2, ... зависит только от автокорреляционной функции основного сигнала S0.

Найдем величину перекрестных помех, определяемых ВКФ сигналов. Для этого перейдем в ограничении (7) в частотную область.

 (13)

где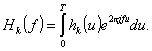

Найдем спектральную функцию первого оператора H1(f). Обозначим через G00(f) спектр мощности основного сигнала S0. Тогда ВКФ сигналов S1 и S2 можно представить [3] в виде

  (14)

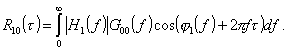
Экстремумам найденной ВКФ будут соответствовать значения t1, удовлетворяющие уравнению

 (15)

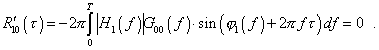
Функции ½H1(f)½и j1(f) оператора A1, доставляющие при t=t1 экстремум функционалу R10(t) с учетом ограничений (13) и (15), будут определяться [4] двумя уравнениями

(16)

  (17)

Уравнение (16) получено путем варьирования функционала R10(t1) по функции½H1(f)½, а уравнение (17) - по функции j1(f).

Умножая левую часть уравнения (16) на функцию½H1(f)½ и интегрируя его в пределах от 0 до ¥, получим, принимая во внимание формулы (13) и (14),

 (18)

Замечая, что cos(j1(f)+2pft1) не может быть равен нулю, и подставляя значение l1f из уравнения (17) в уравнение (16) получим с учетом выражения (18)

 (19)

Умножим уравнение (19) на функцию G00(f) и выполним интегрирование в пределах от 0 до ¥, тогда, с учетом формулы (14), получим

 (20)

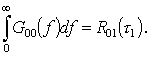
Таким образом, модуль и фаза искомой спектральной функции H1(f) оказываются связанными со спектром мощности основного сигнала S0 следующим соотношением

  (21)

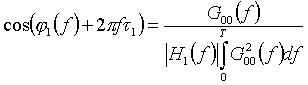
Замечая, что при линейном преобразовании сигнала с некоторой спектральной функцией ½H(f)½2 раз, получаем для спектра мощности сигнала S1

  (22)

Таким образом, при расширении линейной системы сигналов (1), принимая во внимание ограничение (13) и учитывая перекрестные помехи только смежных сигналов в последовательности S1, S2, ..., находим величину перекрестных помех, изменяющуюся по закону

  (23)

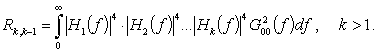
Формула (23) очевидно определяет нижнюю границу перекрестных помех для линейной системы сигналов при отсутствии других внешних помех. Эта формула позволяет сделать еще одно важное предположение: минимум нижней границы перекрестных помех в линейной системе сигналов с фиксированной энергией или средней мощностью достигается на последовательности сигналов (1), отличающихся только фазовыми спектрами, причем

 (24)

где G00(f) - спектр мощности основного сигнала S0.

В качестве основного сигнала может быть выбран любой сигнал. Величина перекрестных помех определяется только спектром мощности основного сигнала S0. Оптимальный выбор спектра сигнала S0 по установленному критерию требует дополнительных исследований. В частности, спектр G00(f) может быть выбран в соответствии с критерием [2].

Возьмем для примера в качестве базового сигнала S1(t) реализацию случайного телеграфного сигнала, принимающего значения ¦1, причем моменты перемены знака сигнала представляют простейший поток событий. Такой сигнал описывается, как известно [3], уравнением Пуассона, а его автокорреляционная функция имеет вид экспоненты

 (25)

где b - удвоенная частота перемены знака.

Как следует из формулы (10), ядро оператора A пропорционально линейной комбинации автокорреляционной функции базового сигнала и ее производной. Поэтому преобразование Фурье функции h1(t) будет иметь в общем случае вид

 (26)

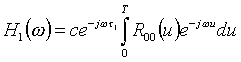
или с учетом формулы (25)

 (27)

где c - некоторая постоянная.

Ограничимся системой сигналов, отличающихся только фазовыми характеристиками или характеристиками, имеющими постоянное значение модуля характеристики Hk(w). В частности, характеристика H1(w)удовлетворяет этому требованию, если a=b, то есть передаточная функция линейного устройства, преобразующего каждый предыдущий сигнал Sk(t) в последующий Sk+1(t), k=0, 1, 2, ...с точностью до несущественных постоянных амплитудных и фазовых множителей будет

 (28)

Такие передаточные функции имеют, как известно [5], линейные ортогональные фильтры, импульсные переходные функции которых gn описываются полиномами Лаггера

 (29)

где

Рассмотрим изменение ВКФ с ростом числа сигналов системы для данного примера. Взаимный спектр сигналов системы имеет [3] вид

 (30)

где G0(w) - спектр мощности базового сигнала или, с учетом формулы (25), и в соответствии с формулой (28)

  (31)

Общий вид ВКФ рассматриваемых сигналов может быть определен путем применения преобразования Фурье к правой части выражения (31)

                     (32)

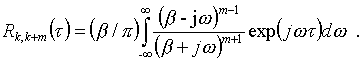
Интегрируя с помощью вычетов, определяем

 (33)

Выводы

1. Установлен алгоритм построения оптимальной по минимуму внутрисистемных помех системы сигналов на базе основного сигнала.

2. Получена зависимость перекрестных помех от спектра мощности основного сигнала и производящих ядер соответствующих линейных интегральных операторов.

3. Установлена нижняя граница минимальной величины перекрестных помех, которая определяется только спектром основного сигнала.

Список литературы

1.ИвановМ.П., КашиновВ.В. Оптимальная частотно-временная фильтрация //  http://www.laboratory.ru/, 2001.

2.ГущинЮ.Е.,КашиновВ.В.,ПономаренкоБ.В. Некоторые свойства оптимальной группы сигналов для асинхронной адресной системы связи. // В сб. "Повышение эффективности и надежности радиоэлектронных систем". Вып. 6, 1976, ЛЭТИ.

3.БендатДж,ПирсолА. Измерение и анализ случайных процессов. М., "Мир", 1971.

4.ИвановМ.П.,КашиновВ.Обобщенный принцип наименьшего действия.  http://www.laboratory.ru/, 2001.

5.ТихоновВ.И. Нелинейные преобразования случайных процессов. // М. Радио и связь, 1986.