Реферат на тему Информация Модели Математическое моделирование
Работа добавлена на сайт bukvasha.net: 2013-11-16Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
РЕФЕРАТ
Тема «Информация. Модели. Математическое моделирование»Выполнил:
Проверил:Новосибирск 2003г.
Содержание
1 Вводные понятия. 32 Классификация моделей. 6
3 Классификация объектов (систем) по их способности использовать информацию. 9
4 Этапы создания модели. 12
5 Понятие о жизненном цикле систем. 13
6 Модели прогнозирования. 15
7 Выводы... 19
Список литературы: 20
Информация. Модели. Математическое моделирование.
1 Вводные понятия.
Под моделированием понимаются методы получения и исследования моделей. Можно дать несколько определений модели.Модель – это некоторый объект, который на разных этапах исследования может заменять исследуемый объект.
Модель – это целевой образ объекта оригинала, отражающий наиболее важные свойства для достижения поставленной цели.
Модель – это либо мысленно представляемая, либо материально реализованная система, которая может отображать или воспроизводить объект исследования, а также замещать его с целью изучения и представления новой информации об объекте. Таким образом, создание каждой модели всегда имеет какую-либо цель.
Под целью понимается конечное состояние, при котором изучаемый объект достигает определенного соответствия во времени и пространстве с другим объектом.
Среди основных целей создания модели можно выделить следующие:
- Гносеологические (познавательные);
- Образовательные;
- Управленческие;
- Экспериментальные;
- Созидательные (проектирование).
Для достижения поставленных целей модель должна обладать некоторыми свойствами, которые одновременно являются и критериями оценки качества построения модели.
Среди свойств модели можно выделить следующие:
- Эффективность;
- Универсальность;
- Устойчивость;
- Содержательность;
- Адекватность;
- Ограниченность;
- Полнота;
- Динамичность.
Свойство эффективности показывает, насколько правильным было создание и использование модели для достижения поставленной цели. Под универсальностью модели понимается возможность её применения в других задачах и для достижения других целей. Устойчивость модели означает её правильную работу в изменяющихся внешних условиях и экстренных ситуациях. Свойство содержательности определяет количество функции модели.
Среди функций модели выделяют описательную, интерпретаторскую, объяснительную, предсказательную, измерительную функции.
Адекватность определяет соответствие модели поставленной задаче. Модель всегда отображает объект-оригинал не во всех его свойствах и функциях. Таким образом, модель является ограниченной. Под полнотой модели понимается наличие сведений об объекте-оригинале, необходимых для достижения поставленной цели. Динамичность определяет изменение модели с течением времени.
История моделирования определяется серединой 20 века, когда была опубликована монография Норберта Винера «Кибернетика или управление и связь в животном и машине».
Важнейшим в моделировании является понятие информации. Под информацией можно понимать следующее:
- Это обозначение содержания полученного из внешнего мира в процессе нашего приспособления к нему. При этом процесс получения и использования информации является процессом нашего приспособления к случайностям нашей среды и нашей жизнедеятельности в этой среде.
- Это совокупность, отчужденная от создателя и обобществленная форма знания.
- Это модель, то есть упрощенное неадекватное представление знаний.
К примеру, информационной моделью знания можно считать текст, закрепленный на материальном носителе. При этом информационная модель позволяет отделить ценную информацию от несущественной, выбрать аналогии среди различных видов объектов и выбрать в качестве рабочей гипотезы одно из возможных решений.
2 Классификация моделей.
Единой классификации моделей не существует, но можно выделить следующие типы моделей:2.1 По способу моделирования:
- Символические или языковые;
- Вещественные или материальные.
2.2 По совпадению природы:
- Физические совпадения;
- Приборные.
2.3 По назначению:
- Гносеологические, для установления законов природы;
- Информационные, для разработки методов управления;
2.4 По способу построения моделей:
- Теоретические (аналитические) – по данным о внутренней структуре;
- Формальные – по зависимости между входом и выходом в систему;
- Комбинированные.
2.5 По типу языка описания:
- Текстовые или дескриптивные;
- Графические (чертежи, схемы);
- Математические;
- Смешанные.
2.6 По зависимости параметров модели от пространственных координат:
- С распределенными переменными (изменяются в пространстве);
- С сосредоточенными переменными (не изменяются в пространстве).
2.7 По зависимости от переменных:
- Независимые;
- Зависимые.
2.8 По принципу построения:
- Стохастические или вероятностные;
- Детерминированные (причинно обусловленные).
2.9 По изменению выходных переменных во времени:
- Статические или стационарные;
- Динамические или нестационарные.
2.10 По приспособляемости модели:
- Адаптивные;
- Неадаптивные
2.11 По способу приспособления, настройки (для адаптивных моделей):
- Поисковые (по минимуму ошибки);
- Беспоисковые.
2.12 По степени соответствия оригиналу:
- Изоморфные (строго соответствующие объекту);
- Гомоморфные (отражает некоторые существенные свойства объекта).
2.13 По природе:
- Материальные или геометрического подобия (фотография);
- Знаковые, в том числе графические и математические;
- Дескриптивная.
2.14 По принципу моделирования:
- Физические модели, в том числе геометрические (модель самолета);
- Аналоговые модели имеют либо сходную структуру со структурой объекта (структурная модель) или выполняют подобные объекту функции (функциональная модель). Принцип аналогии является основным принципом моделирования. Примером аналогии является исследование экономических систем с помощью исследования «потока» электричества в цепи.
- Символические модели – это абстрактные математические уравнения (неравенства).
С помощью данной классификации можно определить модель с разных точек зрения.
В результате современных исследований можно создать управленческую (кибернетическую) модель, в которой отражаются аспекты структурной, функциональной, информационной и математической модели.
При этом любую систему можно изучать на двух уровнях:
- Теоретическом, или фундаментальными методами;
- Эмпирическом, или прикладными методами.
Фундаментальные методы объясняют и предсказывают будущие открытия, а прикладные методы позволяют решать отдельные, не глобальные проблемы.
На эмпирическом уровне система изучается через связи с внешней средой, через свойства и отношения между объектами системами. На первом этапе изучения системы создается дескриптивная модель, которая не содержит управляющих факторов. На втором этапе создается конструктивная модель, которая позволяет выявить существующие факторы с целью эффективного управления ими.
3 Классификация объектов (систем) по их способности использовать информацию.
Система представляет собой ограниченное и взаимосвязанное единство различных объектов живой и неживой природы.Пользуясь данной классификацией можно выделить 7 типов систем:
3.1 Простое преобразование.
| O |
| I |
 |
где, I – входная информация;
O – выходная информация.
Собственная цель отсутствует. Непрерывные указания идут от внешнего источника, и при этом реализуются 3 операции:
- прием;
- переработка, или преобразование;
- выходное воздействие.
Пример: процесс превращения заказа в товары, звуковые усилители.
3.2 Простая сортировка.
| O1 |
| I |
| O2 |

Система имеет два выхода и один вход. Правила сортировки реализованы в блоке преобразования. Это простые операции поиска и распознавания.
3.3 Обратная связь.
| O |
| I |
| А |
| С |
| В |

А – блок получения ошибки.
С – блок формирование сигнала обратной связи.
В – исполнительный механизм.
Дуга СА – обратная связь.
Дуга АВ – ошибка.
Часть выходного сигнала сравнивается с установленным на входе сигналом, и анализируются рассогласования. Обычно обратная связь уменьшает ошибку и называется отрицательной обратной связью, так как направлена противоположно действию. Примером является система планирования, где анализируется устойчивость, время запаздывания и осуществляется контроль. Также примером является движение антенны радара.
3.4 Сортировка с обратной связью.
| O1 |
| I |
| O2 |

3.5 Система с автоматическим изменением цели, или обратная связь второго порядка.
| A |
| B |
| C |
| D |
| E |

В этой системе реализуется выбор при изменении внешних условий.
А – рецептор.
B – эффектор.
С – принятие решений.
D – выборка из памяти.
E – память.
По такой схеме реализуется процесс обучения любой организации.
3.6 Система с сознательным изменением цели, или обратная связь третьего порядка.
| A |
| B |
| C |
| D |
| E |
| F |

F – переработка информации.
Сознание – это представление об объекте, о цели, об управлении рецептором и эффектором; о процессах, связанных с памятью.
Память – это коллективное знание, где реализуются хранение, поиск, обработка данных.
В этих системах из большого объема внешней информации выбирается такая, которая необходима субъекту (человеку, организации). Такая система может управлять собственным ростом и развитием.
3.7 Комбинированные.
1
2
3
4
5
6
7
8
 4 Этапы создания модели.
4 Этапы создания модели.
1 – система (объект, явление, процесс).| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
2 – описание системы.
3 – постановка задачи.
4 – математическая модель.
5 – непротиворечивость выводов в рамках модели.
6 – решение задачи.
7 – проверка адекватности
8 – уточнение модели.
При изучении любого объекта путем моделирования нужно выполнять ряд обязательных, вышеперечисленных этапов.
Дуга (1 – 2) – наблюдение эксперимента.
Дуга (2 – 3) – формализация абстракции, то есть описание существенных факторов и связей между ними.
Дуга (3 – 4) – конструирование элементов модели.
Дуга (4 – 5) – изучение модели.
Дуга (5 – 6) – выбор методов решения.
Дуга (6 – 7) – сравнение выводов с реальными фактами.
Решение, полученное на модели, действительно только до тех пор, пока неуправляемые параметры сохраняют свои значения, и соотношения между параметрами модели остаются постоянными. Если решение выходит из-под контроля, то теряется возможность управления им, тогда устанавливается процедура подстройки решения.
Так как модель всегда лишь частично отображает действительность, то она может быть хорошей, если будет точно предсказывать влияние изменений в системе на общую эффективность всей системы. Решение можно оценить, сопоставив результаты, полученные по модели, с ранее полученными данными, или с данными практических испытаний.
Многокритериальные задачи обычно решаются как последовательность однокритериальных задач. Критерий оптимизации, в данном случае, называется целевой функцией. Затем формируются ограничения, и выбирается один из следующих методов решения:
- Дедуктивный, или аналитический.
- Индуктивный, или численный.
- Метод Монте-Карло, или статистических испытаний.
5 Понятие о жизненном цикле систем.
Под жизненным циклом любой системы понимается промежуток времени, который проходит между осознанием необходимости в этом изделии и осознании его ненужности. Между этими моментами существует ряд этапов. К примеру, в экономике это следующая последовательность:
- Маркетинг.
- Проектирование и разработка.
- Материально-техническое снабжение производственных процессов.
- Подготовка и разработка технологических процессов.
- Производство.
- Контроль, проведение испытаний и наблюдений.
- Упаковка и хранение.
- Реализация изделия.
- Монтаж, эксплуатация.
- Техническая помощь.
- Утилизация.
Модель объекта должна строиться так, чтобы любой фрагмент был доступен на каждом этапе жизненного цикла.
Взаимодействие модели и объекта исследования происходит на нескольких этапах:
- Моделирование в виртуальном мире объектов реального мира.
- Создание и развитие виртуального мира.
- Воплощение объектов виртуального мира в реальном мире.
Z – вектор контролируемых возмущений.
Y – неконтролируемый вектор выходных параметров.
U – контролируемый вектор управляющих воздействий на технологический процесс.
W – вектор неконтролируемых возмущений.
Затем выполняется формализация, и объект представляется в следующем виде:
Y – вектор выходных параметров.
X – вектор контролируемых входных переменных. (Объединяет действия переменных U, Z).
E – случайная аддитивная помеха (суммарная), которая характеризует влияние случайных возмущений.
F (B,x) – параметрическая функция, которая осуществляет преобразование значений Х в Y, или это модель изучаемого объекта.
Предметом исследования модели является определение вида модели и параметров модели. Истинного значения параметров системы узнать невозможно, можно получить только оценку параметров любой модели (вектора В). Изменяя значения параметров Х можно наблюдать изменение поведения выходных значений Y, или поддерживать Y на постоянном уровне.
Изменение Х определяется либо объективными возможностями существования данного фактора, либо нормативами. Чем меньше количество управляемых факторов, тем лучше управлять системой в целом.
Входные параметры считаются независимыми, или экзогенными.
Выходные параметры считаются зависимыми, или эндогенными.
- Статистические методы.
- Методы аналогии.
К статистическим методам относятся аппроксимация, интерполяция, , методы исследования временных рядов.
К методам аналогии относятся модели планирования эксперимента, а также математические, исторические и другие аналогии.
Среди моделей прогнозирования можно выделить следующие:
6.1 Модели аппроксимации.
Методы аппроксимации применимы к детерминированным и статистическим системам.
Аппроксимация – приближение (с лат.).
Выбор аппроксимирующей функции F(B,x) связан с решением оптимизационной задачи. Для этого применяется критерий минимизации квадратичной ошибки.
Постановка задачи.
Пусть проведено N(xI,yI) опытов, где
xI - входной параметр;
yI - выходной параметр.
Необходимо подобрать модель связывающую x и y.
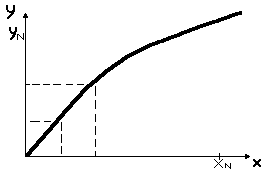
Через точки (xI,yI) можно провести кривую, которая, в свою очередь, может проходить через эти точки или находиться вблизи данных точек.
В аппроксимации для получения параметров модели используется МНК-критерий (метод наименьших квадратов). Лучшей считается та модель, для которой сумма квадратов отклонений опытных значений, от теоретических будет минимальной.
Для этого формируется целевая функция или критерий оптимизации.
S = ∑ (yI – F(B, xI))2 – min.
Далее надо исследовать функцию на экстремум. Неизвестными будут коэффициенты модели B. Наиболее просто находятся параметры, если F(B, xI) представляет собой полином n-ной степени. При этом формируется система линейных уравнений, порядок которой на единицу больше степени полинома.
К примеру, для полинома 3-ей степени система будет выглядеть так:


 N ∑ xI ∑ xI2 ∑ yI b0
N ∑ xI ∑ xI2 ∑ yI b0
С = ∑ xI ∑ xI2 ∑ xI3 D = ∑ xI yI B = b1
∑ xI2 ∑ xI3 ∑ xI4 ∑ xI2 yI b2
C – матрица коэффициентов системы.
D – вектор-столбец свободных членов.
B – вектор неизвестных.
В общем случае для нахождения параметров формируется система дифференциальных уравнений. В конце формируется система линейных уравнений, которую можно решать точными методами (метод Крамера, Гауса, обратной матрицы). Когда система решена, то есть, найдены параметры модели, можно выполнить прогнозирование значений y.
Если выбираемое x находится внутри элементарного интервала ∆x, то говорят о прогнозировании в настоящем. Если x меньше x0, или x больше xN, то речь идет об экстраполяции.
6.2 Модели интерполяции.
В интерполяции, в отличие от аппроксимации, производится минимизация линейной ошибки. Также, в отличие от аппроксимации, где кривая по отношению к точкам опытов может располагаться любым образом, а именно находиться вблизи этих точек, или проходить через некоторые из них, кривая интерполяции, или интерполяционный полином обязательно проходит через все точки кривой, которые называются узлами.
Наиболее простой подход к получению интерполяционной модели был предложен Лагранжем. Так как полином проходит через каждую опытную точку, то нужно составить столько уравнений, сколько проведено опытов. В левой части уравнения формируется полином, проходящий через i-тую точку. В правой части формируется вектор значений y. В результате получается система линейных уравнений n-ого порядка, где n – число опытов, а степень интерполяционного полинома на единицу меньше числа опытов.
Количество опытов должно обязательно быть больше пяти, иначе результаты интерполирования будут не пригодны для прогнозирования. Так как метод интерполяции требует прохождения модели через все точки, то накладываются определенные условия на опытные значения. Разности i-ого порядка должны быть примерно одинаковы малы. Хорошо интерполируются монотонные функции.
Оба рассмотренных метода относятся к методам исследования детерминированных моделей.
6.3 Анализ временных рядов.
Временные ряды отражают тенденцию изменения параметров системы во времени, поэтому входным параметром х является момент времени.
Выходной параметр y называется уровнем ряда. В случае отсутствия ярко выраженных изменений в течение времени, общая тенденция сохраняется. Ряд можно описать уравнением вида
YT = F (t) + ET , где
F (t) – детерминированная функция времени.
ET – случайная величина
Во временных рядах проводится операция анализа и сглаживания тренда, который отражает влияние некоторых факторов. Для построения тренда применяется МНК-критерий.
Существуют моментальные и интервальные ряды. В моментальных рядах отражаются абсолютные величины, по состоянию на определенный момент времени, а в интервальных – относительные величины (показатель за год, месяц, и т.д.). Исследование данных при помощи рядов позволяет во многих случаях более четко представить детерминированную функцию. При этом рассчитываются базисные и цепные показатели (прирост, коэффициент роста, коэффициент роста, темп роста, темп прироста, и др.). Под базисными показателями понимают, показатели, которые соотносятся к начальному уровню ряда. Цепные показатели относятся к предыдущему уровню.
Прогноз явлений по временным рядам состоит из двух этапов:
- Прогноз детерминированной компоненты.
- Прогноз случайной компоненты.
Обе проблемы связаны с анализом результатов парных экспериментов. В отличие от аппроксимации и интерполяции анализ временных рядов включает в себя методы оценки случайных компонент. Поэтому прогнозирование при помощи временных рядов является более точным.
Исследование рядов имеет большое значение и для технических, и для экономических систем.
Новая информация может быть получена путем наблюдения, то есть, изучением системы без вмешательства в её функционирование. Также она может быть получена путем эксперимента, то есть, изучая систему при целенаправленном воздействии на её параметры.
Модель исследуется для того, чтобы можно было управлять исследуемым объектом или системой, на основании полученной по модели информации. Управление системы связано с улучшением его характеристик или её стабилизацией, то есть с возможностью прогнозирования поведения систем.
Ивченко Б. П., Мартыщенко Л.А. Информационная микроэкономика Часть 1: Методы анализа и прогнозирования. СПб. Нордмед-Издат. 1997г.
Турчак К. Численные методы. М.- 1985г.
Шелобаев С.И. Математические методы и модели в экономике, финансах и бизнесе: Учеб. Пособие для вузов. М.- 2000г.
Черчмен У., Акоф Р., Арноф Я. Введение в исследование операции М. – Наука 1968г.
- Маркетинг.
- Проектирование и разработка.
- Материально-техническое снабжение производственных процессов.
- Подготовка и разработка технологических процессов.
- Производство.
- Контроль, проведение испытаний и наблюдений.
- Упаковка и хранение.
- Реализация изделия.
- Монтаж, эксплуатация.
- Техническая помощь.
- Утилизация.
Модель объекта должна строиться так, чтобы любой фрагмент был доступен на каждом этапе жизненного цикла.
Взаимодействие модели и объекта исследования происходит на нескольких этапах:
- Моделирование в виртуальном мире объектов реального мира.
- Создание и развитие виртуального мира.
- Воплощение объектов виртуального мира в реальном мире.
W
Z
Y
U
 Любой объект можно представить как «черный ящик», на который воздействуют различные факторы.
Любой объект можно представить как «черный ящик», на который воздействуют различные факторы.
Z – вектор контролируемых возмущений. | W |
| Z |
| Y |
| U |
Y – неконтролируемый вектор выходных параметров.
U – контролируемый вектор управляющих воздействий на технологический процесс.
W – вектор неконтролируемых возмущений.
Затем выполняется формализация, и объект представляется в следующем виде:
| F (B,x) |
| Y |
| X |
| E |
| |
 |
Y – вектор выходных параметров.
X – вектор контролируемых входных переменных. (Объединяет действия переменных U, Z).
E – случайная аддитивная помеха (суммарная), которая характеризует влияние случайных возмущений.
F (B,x) – параметрическая функция, которая осуществляет преобразование значений Х в Y, или это модель изучаемого объекта.
Предметом исследования модели является определение вида модели и параметров модели. Истинного значения параметров системы узнать невозможно, можно получить только оценку параметров любой модели (вектора В). Изменяя значения параметров Х можно наблюдать изменение поведения выходных значений Y, или поддерживать Y на постоянном уровне.
Изменение Х определяется либо объективными возможностями существования данного фактора, либо нормативами. Чем меньше количество управляемых факторов, тем лучше управлять системой в целом.
Входные параметры считаются независимыми, или экзогенными.
Выходные параметры считаются зависимыми, или эндогенными.
6 Модели прогнозирования.
Существует множество математических моделей, посредством которых решаются те, или иные задачи. Во всех сферах деятельности человека важным моментом является прогнозирование последующих событий. Сейчас существует более 100 методов и методик прогнозирования, Условно их можно разделить на фактографические и экспертные. Фактографические методы основаны на анализе информации об объекте, а экспертные – на суждениях экспертов, которые получены при проведении коллективных или индивидуальных опросов. Среди фактографических методов можно выделить следующие:- Статистические методы.
- Методы аналогии.
К статистическим методам относятся аппроксимация, интерполяция, , методы исследования временных рядов.
К методам аналогии относятся модели планирования эксперимента, а также математические, исторические и другие аналогии.
Среди моделей прогнозирования можно выделить следующие:
6.1 Модели аппроксимации.
Методы аппроксимации применимы к детерминированным и статистическим системам.
Аппроксимация – приближение (с лат.).
Выбор аппроксимирующей функции F(B,x) связан с решением оптимизационной задачи. Для этого применяется критерий минимизации квадратичной ошибки.
Постановка задачи.
Пусть проведено N(xI,yI) опытов, где
xI - входной параметр;
yI - выходной параметр.
Необходимо подобрать модель связывающую x и y.

Через точки (xI,yI) можно провести кривую, которая, в свою очередь, может проходить через эти точки или находиться вблизи данных точек.
В аппроксимации для получения параметров модели используется МНК-критерий (метод наименьших квадратов). Лучшей считается та модель, для которой сумма квадратов отклонений опытных значений, от теоретических будет минимальной.
Для этого формируется целевая функция или критерий оптимизации.
S = ∑ (yI – F(B, xI))2 – min.
Далее надо исследовать функцию на экстремум. Неизвестными будут коэффициенты модели B. Наиболее просто находятся параметры, если F(B, xI) представляет собой полином n-ной степени. При этом формируется система линейных уравнений, порядок которой на единицу больше степени полинома.
К примеру, для полинома 3-ей степени система будет выглядеть так:
С = ∑ xI ∑ xI2 ∑ xI3 D = ∑ xI yI B = b1
∑ xI2 ∑ xI3 ∑ xI4 ∑ xI2 yI b2
C – матрица коэффициентов системы.
D – вектор-столбец свободных членов.
B – вектор неизвестных.
В общем случае для нахождения параметров формируется система дифференциальных уравнений. В конце формируется система линейных уравнений, которую можно решать точными методами (метод Крамера, Гауса, обратной матрицы). Когда система решена, то есть, найдены параметры модели, можно выполнить прогнозирование значений y.
Если выбираемое x находится внутри элементарного интервала ∆x, то говорят о прогнозировании в настоящем. Если x меньше x0, или x больше xN, то речь идет об экстраполяции.
6.2 Модели интерполяции.
В интерполяции, в отличие от аппроксимации, производится минимизация линейной ошибки. Также, в отличие от аппроксимации, где кривая по отношению к точкам опытов может располагаться любым образом, а именно находиться вблизи этих точек, или проходить через некоторые из них, кривая интерполяции, или интерполяционный полином обязательно проходит через все точки кривой, которые называются узлами.
Наиболее простой подход к получению интерполяционной модели был предложен Лагранжем. Так как полином проходит через каждую опытную точку, то нужно составить столько уравнений, сколько проведено опытов. В левой части уравнения формируется полином, проходящий через i-тую точку. В правой части формируется вектор значений y. В результате получается система линейных уравнений n-ого порядка, где n – число опытов, а степень интерполяционного полинома на единицу меньше числа опытов.
Количество опытов должно обязательно быть больше пяти, иначе результаты интерполирования будут не пригодны для прогнозирования. Так как метод интерполяции требует прохождения модели через все точки, то накладываются определенные условия на опытные значения. Разности i-ого порядка должны быть примерно одинаковы малы. Хорошо интерполируются монотонные функции.
Оба рассмотренных метода относятся к методам исследования детерминированных моделей.
6.3 Анализ временных рядов.
Временные ряды отражают тенденцию изменения параметров системы во времени, поэтому входным параметром х является момент времени.
Выходной параметр y называется уровнем ряда. В случае отсутствия ярко выраженных изменений в течение времени, общая тенденция сохраняется. Ряд можно описать уравнением вида
YT = F (t) + ET , где
F (t) – детерминированная функция времени.
ET – случайная величина
Во временных рядах проводится операция анализа и сглаживания тренда, который отражает влияние некоторых факторов. Для построения тренда применяется МНК-критерий.
Существуют моментальные и интервальные ряды. В моментальных рядах отражаются абсолютные величины, по состоянию на определенный момент времени, а в интервальных – относительные величины (показатель за год, месяц, и т.д.). Исследование данных при помощи рядов позволяет во многих случаях более четко представить детерминированную функцию. При этом рассчитываются базисные и цепные показатели (прирост, коэффициент роста, коэффициент роста, темп роста, темп прироста, и др.). Под базисными показателями понимают, показатели, которые соотносятся к начальному уровню ряда. Цепные показатели относятся к предыдущему уровню.
Прогноз явлений по временным рядам состоит из двух этапов:
- Прогноз детерминированной компоненты.
- Прогноз случайной компоненты.
Обе проблемы связаны с анализом результатов парных экспериментов. В отличие от аппроксимации и интерполяции анализ временных рядов включает в себя методы оценки случайных компонент. Поэтому прогнозирование при помощи временных рядов является более точным.
Исследование рядов имеет большое значение и для технических, и для экономических систем.
7 Выводы
Любая информация может быть получена на основании прошлого опыта, а именно теории проверенной практикой (научные факты, методики и расчеты, опыт каждого человека).Новая информация может быть получена путем наблюдения, то есть, изучением системы без вмешательства в её функционирование. Также она может быть получена путем эксперимента, то есть, изучая систему при целенаправленном воздействии на её параметры.
Модель исследуется для того, чтобы можно было управлять исследуемым объектом или системой, на основании полученной по модели информации. Управление системы связано с улучшением его характеристик или её стабилизацией, то есть с возможностью прогнозирования поведения систем.
Список литературы:
Губарев В.В. Концептуальные основы информатики: Учеб. Пособие: Новосибирск: Изд-во НГТУ, 2001г.Ивченко Б. П., Мартыщенко Л.А. Информационная микроэкономика Часть 1: Методы анализа и прогнозирования. СПб. Нордмед-Издат. 1997г.
Турчак К. Численные методы. М.- 1985г.
Шелобаев С.И. Математические методы и модели в экономике, финансах и бизнесе: Учеб. Пособие для вузов. М.- 2000г.
Черчмен У., Акоф Р., Арноф Я. Введение в исследование операции М. – Наука 1968г.