Реферат на тему Коды Боуза Чоудхури Хоквингема
Работа добавлена на сайт bukvasha.net: 2015-01-08Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
РЕФЕРАТ
По курсу “Теория информации и кодирования”
на тему:
"КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА"
БЧХ коды
Коды Боуза-Чоудхури-Хоквингема (БЧХ) – класс циклических кодов, исправляющих кратные ошибки, т. е. две и более (d0 ³ 5).
Теоретически коды БЧХ могут исправлять произвольное количество ошибок, но при этом существенно увеличивается длительность кодовой комбинации, что приводит к уменьшению скорости передачи данных и усложнению приемо-передающей аппаратуры (схем кодеров и декодеров).
Методика построения кодов БЧХ отличается от обычных циклических, в основном, выбором определяющего полинома P(х). Коды БЧХ строятся по заданной длине кодового слова n и числа исправляемых ошибок S , при этом количество информационных разрядов k не известно пока не выбран определяющий полином.
Рассмотрим процедуру кодирования с использованием кода БЧХ на конкретных примерах.
Пример Построить 15-разрядный код БЧХ, исправляющий две ошибки в кодовой комбинации (т. е. n = 15, S = 2).
Решение:
1. Определим количество контрольных m и информационных разрядов k
m £ h S .
Определим параметр h из формулы
n = 2h-1, h = log2(n+1) = log216 = 4,
при этом: m £ h S = 4×2 = 8; k = n-m = 15-8 = 7.
Таким образом, получили (15, 7)-код.
2. Определим параметры образующего полинома:
- количество минимальных многочленов, входящих в образующий
L = S = 2;
- порядок старшего (все минимальные - нечетные) минимального многочлена r = 2S-1 = 3;
- степень образующего многочленаb = m £ 8.
3. Выбор образующего многочлена.
Из таблицы для минимальных многочленов для кодов БЧХ (см. приложение 4) из колонки 4 (т. к. l = h = 4) выбираем два минимальных многочлена 1 и 3 (т. к. r = 3):
M1(x) = 10011;
M2(x) = 11111.
При этом
P(x) =M1(x)×M2(x)=10011´11111=111010001= x8+ x7+ x6+ x4+1.
4. Строим образующую матрицу. Записываем первую строку образующей матрицы, которая состоит из образующего полинома с предшествующими нулями, при этом общая длина кодовой комбинации равна n = 15. Остальные строки матрицы получаем в результате k-кратного циклического сдвига справа налево первой строки матрицы.

Строки образующей матрицы представляют собой 7 кодовых комбинаций кода БЧХ, а остальные могут быть получены путем суммирования по модулю 2 всевозможных сочетаний строк матрицы.
Процедура декодирования, обнаружения и исправления ошибок в принятой кодовой комбинации такая же, как и для циклических кодов с d0 < 5
Пример Построить 31-разрядный код БЧХ, исправляющий три ошибки в кодовой комбинации (т. е. n = 31, S = 3).
Решение:
1. Определим количество контрольных разрядов m и информационных разрядов k.
m £ h S.
Определим параметр h из формулы
n = 2h-1,h = log2(n+1) = log232 = 5,
при этом: m £ h S = 5×3 = 15; k = n-m = 31-15 = 16.
Таким образом, получили (31, 16)-код.
2.Определим параметры образующего полинома:
- количество минимальных многочленов, входящих в образующий
L = S = 3;
- порядок старшего минимального многочлена
r = 3S-1 = 5;
- степень образующего многочлена
b = m £ 15.
1. Выбор образующего многочлена.
Из таблицы для минимальных многочленов для кодов БЧХ ( приложение 4) из колонки 5 (т. к. l = h = 5) выбираем три минимальных многочлена 1, 3 и 5 (т. к. r = 5):
M1(x) =100101;
M2(x) =111101;
M3(x) =110111.
При этом
P(x) = M1(x) ×M2(x) ×M3(x) =1000111110101111=
= x15+ x11 +x10+ x9+ x8+ x7+ x5+ x3 + x2+x+ 1.
4. Строим образующую матрицу. Записываем первую строку образующей матрицы, которая состоит из образующего полинома с предшествующими нулями, при этом общая длина кодовой комбинации равна n = 31. Остальные строки матрицы получаем в результате k-кратного циклического сдвига справа налево первой строки матрицы.
000000000000000100011111011111
G(31,16)=000000000000001000111110111110
. . .
100011111011111000000000000000
Строки образующей матрицы представляют собой 16 кодовых комбинации кода БЧХ, а остальные могут быть получены путем суммирования по модулю 2 всевозможных сочетаний строк матрицы.
Декодирование кодов БЧХ
Коды БЧХ представляют собой циклические коды и, следовательно, к ним применимы любые методы декодирования циклических кодов. Открытие кодов БЧХ привело к необходимости поиска новых алгоритмов и методов реализации кодеров и декодеров. Получены существенно лучшие алгоритмы, специально разработанные для кодов БЧХ. Это алгоритмы Питерсона, Бэрлекэмпа и др.
Рассмотрим алгоритм ПГЦ (Питерсона-Горенстейна-Цирлера). Пусть БЧХ код над полем GF(q) длины n и с конструктивным расстоянием d задается порождающим полиномом g(x), который имеет среди своих корней элементы
Можно составить j-ый синдром Sj принятого слова r(x):
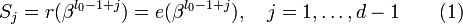 .
.
Задача состоит в нахождений числа ошибок u, их позиций 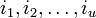 и их значений
и их значений 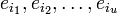 при известных синдромах Sj.
при известных синдромах Sj.
Предположим, для начала, что u в точности равно t. Запишем (1) в виде системы нелинейных уравнений в явном виде:
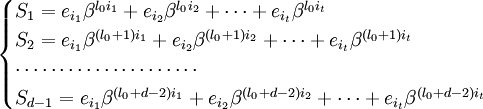
Обозначим через 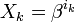 локатор k-ой ошибки, а через
локатор k-ой ошибки, а через 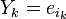 величину ошибки,
величину ошибки, 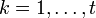 . При этом все Xk различны, так как порядок элемента β равен n, и поэтому при известном Xk можно определить ik как ik = logβXk.
. При этом все Xk различны, так как порядок элемента β равен n, и поэтому при известном Xk можно определить ik как ik = logβXk.
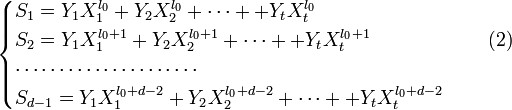
Составим полином локаторов ошибок:
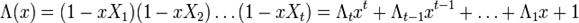
Корнями этого полинома являются элементы, обратные локаторам ошибок. Помножим обе части этого полинома на 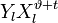 . Полученное равенство будет справедливо для
. Полученное равенство будет справедливо для
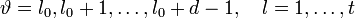 :
:
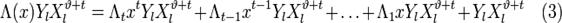
Положим 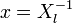 и подставим в (3). Получится равенство, справедливое для каждого
и подставим в (3). Получится равенство, справедливое для каждого 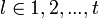 и при всех
и при всех 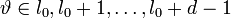 :
:
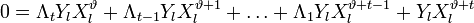
Таким образом для каждого l можно записать свое равенство. Если их просуммировать по l, то получиться равенство, справедливое для каждого
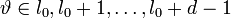 :
:
 .
.
Учитывая (2) и то, что
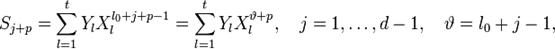
(то есть 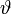 меняется в тех же пределах, что и ранее) получаем систему линейных уравнений:
меняется в тех же пределах, что и ранее) получаем систему линейных уравнений:
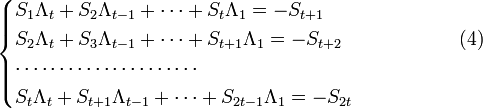
.
Или в матричной форме
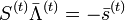 ,
,
Где
![S^{(t)}={ \left[ \begin{matrix}S_1 & S_2 & \dots & S_t \\S_2 & S_3 & \dots & S_{t+1} \\\cdots & \cdots & \cdots & \\S_t & S_{t+1} & \dots & S_{2t-1} \end{matrix} \right] }, \quad \quad \quad \quad \quad\quad(5)](https://bukvasha.net/img/32/dopb313187.zip)
![\bar\Lambda^{(t)} = { \left[ \begin{matrix}\Lambda_t \\\Lambda_{t-1} \\\cdots \\\Lambda_1\end{matrix} \right] }, \quad \quad \bar s^{(t)}{ \left[ \begin{matrix}S_{t+1} \\S_{t+2} \\\cdots \\S_{2t}\end{matrix} \right] }](https://bukvasha.net/img/32/dopb313188.zip)
Если число ошибок и в самом деле равно t, то система (4) разрешима, и можно найти значения коэффициентов 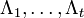 . Если же число u < t, то определитель матрицы S(t) системы (4) будет равен 0. Это есть признак того, что количество ошибок меньше t. Поэтому необходимо составить систему (4), предполагая число ошибок равным t − 1. Высчитать определитель новой матрицы S(t − 1) и т. д., до тех пор, пока не установим истинное число ошибок.
. Если же число u < t, то определитель матрицы S(t) системы (4) будет равен 0. Это есть признак того, что количество ошибок меньше t. Поэтому необходимо составить систему (4), предполагая число ошибок равным t − 1. Высчитать определитель новой матрицы S(t − 1) и т. д., до тех пор, пока не установим истинное число ошибок.
После этого можно решить систему (4) и получить коэффициенты полинома локаторов ошибок. Его корни (элементы, обратные локаторам ошибок) можно найти простым перебором по всем элементам поля GF(qm). К ним найти элементы, обратные по умножению, — это локаторы ошибок 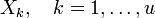 . По локаторам можно найти позиции ошибок (ik = logβXk), а значения Yk ошибок из системы (2), приняв t = u. Декодирование завершено.
. По локаторам можно найти позиции ошибок (ik = logβXk), а значения Yk ошибок из системы (2), приняв t = u. Декодирование завершено.
Коды Рида–Соломона
Широко используемым подмножеством кодов БЧХ являются коды Рида-Соломона, которые позволяют исправлять пакеты ошибок. Пакет ошибок длины b представляет собой последовательность из таких b ошибочных символов, что первый и последний из них отличны от нуля. Существуют классы кодов Рида-Соломона, позволяющие исправлять многократные пакеты ошибок.
Кроме рассмотренных корректирующих кодов используются так называемые сверточные коды, контрольные биты, в которых формируются непрерывно из информационных и контрольных бит смежных блоков.
Выводы
Таким образом, в результате написания реферата, пришли к выводу, что коды Боуза-Чоудхури-Хоквингхема – это широкий класс циклических кодов, способных исправлять многократные ошибки.
БЧХ-коды играют заметную роль в теории и практике кодирования. Интерес к ним определяется следующим: коды БЧХ имеют весьма хорошие свойства; данные коды имеют относительно простые методы кодирования и декодирования; коды Рида-Соломона являются широко известным подклассом недвоичных БЧХ кодов, которые обладают оптимальными свойствами, и применяются для исправления многократных пакетов ошибок.
Список использованной литературы
1. Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and practice of error control codes. — М.: Мир, 1986. — С. 576
2. Дмитриев В.И. Прикладная теория информации: Учебник для вузов. М.: Высшая школа , 1989. 320 c.
3. Колесник В.Д., Полтырев Г.Ш. Курс теории информации. – М.: Наука, 1982.
4. Кудряшов Б.Д. Теория информации. Учебник для вузов Изд-во ПИТЕР, 2008. – 320с.
5. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. — М.: Мир, 1976. — С. 596.
6. Семенюк В. В. Экономное кодирование дискретной информации. – СПб.: СПб ГИТМО (ТУ), 2001
7. У. Петерсон, Э. Уэлдон, Коды, исправляющие ошибки, Москва, “Мир”, 1976.
8. Э. Берлекэмп, Алгебраическая теория кодирования, Москва, “Мир”, 1971.
По курсу “Теория информации и кодирования”
на тему:
"КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА"
БЧХ коды
Коды Боуза-Чоудхури-Хоквингема (БЧХ) – класс циклических кодов, исправляющих кратные ошибки, т. е. две и более (d0 ³ 5).
Теоретически коды БЧХ могут исправлять произвольное количество ошибок, но при этом существенно увеличивается длительность кодовой комбинации, что приводит к уменьшению скорости передачи данных и усложнению приемо-передающей аппаратуры (схем кодеров и декодеров).
Методика построения кодов БЧХ отличается от обычных циклических, в основном, выбором определяющего полинома P(х). Коды БЧХ строятся по заданной длине кодового слова n и числа исправляемых ошибок S , при этом количество информационных разрядов k не известно пока не выбран определяющий полином.
Рассмотрим процедуру кодирования с использованием кода БЧХ на конкретных примерах.
Пример Построить 15-разрядный код БЧХ, исправляющий две ошибки в кодовой комбинации (т. е. n = 15, S = 2).
Решение:
1. Определим количество контрольных m и информационных разрядов k
m £ h S .
Определим параметр h из формулы
n = 2h-1, h = log2(n+1) = log216 = 4,
при этом: m £ h S = 4×2 = 8; k = n-m = 15-8 = 7.
Таким образом, получили (15, 7)-код.
2. Определим параметры образующего полинома:
- количество минимальных многочленов, входящих в образующий
L = S = 2;
- порядок старшего (все минимальные - нечетные) минимального многочлена r = 2S-1 = 3;
- степень образующего многочленаb = m £ 8.
3. Выбор образующего многочлена.
Из таблицы для минимальных многочленов для кодов БЧХ (см. приложение 4) из колонки 4 (т. к. l = h = 4) выбираем два минимальных многочлена 1 и 3 (т. к. r = 3):
M1(x) = 10011;
M2(x) = 11111.
При этом
P(x) =M1(x)×M2(x)=10011´11111=111010001= x8+ x7+ x6+ x4+1.
4. Строим образующую матрицу. Записываем первую строку образующей матрицы, которая состоит из образующего полинома с предшествующими нулями, при этом общая длина кодовой комбинации равна n = 15. Остальные строки матрицы получаем в результате k-кратного циклического сдвига справа налево первой строки матрицы.

Строки образующей матрицы представляют собой 7 кодовых комбинаций кода БЧХ, а остальные могут быть получены путем суммирования по модулю 2 всевозможных сочетаний строк матрицы.
Процедура декодирования, обнаружения и исправления ошибок в принятой кодовой комбинации такая же, как и для циклических кодов с d0 < 5
Пример Построить 31-разрядный код БЧХ, исправляющий три ошибки в кодовой комбинации (т. е. n = 31, S = 3).
Решение:
1. Определим количество контрольных разрядов m и информационных разрядов k.
m £ h S.
Определим параметр h из формулы
n = 2h-1,h = log2(n+1) = log232 = 5,
при этом: m £ h S = 5×3 = 15; k = n-m = 31-15 = 16.
Таким образом, получили (31, 16)-код.
2.Определим параметры образующего полинома:
- количество минимальных многочленов, входящих в образующий
L = S = 3;
- порядок старшего минимального многочлена
r = 3S-1 = 5;
- степень образующего многочлена
b = m £ 15.
1. Выбор образующего многочлена.
Из таблицы для минимальных многочленов для кодов БЧХ ( приложение 4) из колонки 5 (т. к. l = h = 5) выбираем три минимальных многочлена 1, 3 и 5 (т. к. r = 5):
M1(x) =100101;
M2(x) =111101;
M3(x) =110111.
При этом
P(x) = M1(x) ×M2(x) ×M3(x) =1000111110101111=
= x15+ x11 +x10+ x9+ x8+ x7+ x5+ x3 + x2+x+ 1.
4. Строим образующую матрицу. Записываем первую строку образующей матрицы, которая состоит из образующего полинома с предшествующими нулями, при этом общая длина кодовой комбинации равна n = 31. Остальные строки матрицы получаем в результате k-кратного циклического сдвига справа налево первой строки матрицы.
000000000000000100011111011111
G(31,16)=000000000000001000111110111110
. . .
100011111011111000000000000000
Строки образующей матрицы представляют собой 16 кодовых комбинации кода БЧХ, а остальные могут быть получены путем суммирования по модулю 2 всевозможных сочетаний строк матрицы.
Декодирование кодов БЧХ
Коды БЧХ представляют собой циклические коды и, следовательно, к ним применимы любые методы декодирования циклических кодов. Открытие кодов БЧХ привело к необходимости поиска новых алгоритмов и методов реализации кодеров и декодеров. Получены существенно лучшие алгоритмы, специально разработанные для кодов БЧХ. Это алгоритмы Питерсона, Бэрлекэмпа и др.
Рассмотрим алгоритм ПГЦ (Питерсона-Горенстейна-Цирлера). Пусть БЧХ код над полем GF(q) длины n и с конструктивным расстоянием d задается порождающим полиномом g(x), который имеет среди своих корней элементы 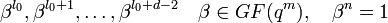 ,
, 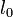 — целое число (например 0 или 1). Тогда каждое кодовое слово обладает тем свойством, что
— целое число (например 0 или 1). Тогда каждое кодовое слово обладает тем свойством, что 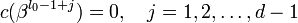 . Принятое слово r(x) можно записать как r(x) = c(x) + e(x), где e(x) — полином ошибок. Пусть произошло
. Принятое слово r(x) можно записать как r(x) = c(x) + e(x), где e(x) — полином ошибок. Пусть произошло 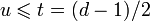 ошибок на позициях
ошибок на позициях 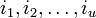 (t максимальное число исправляемых ошибок), значит
(t максимальное число исправляемых ошибок), значит 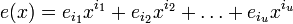 , а
, а 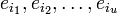 — величины ошибок.
— величины ошибок.
Можно составить j-ый синдром Sj принятого слова r(x): Задача состоит в нахождений числа ошибок u, их позиций
Предположим, для начала, что u в точности равно t. Запишем (1) в виде системы нелинейных уравнений в явном виде:
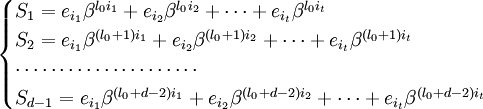
Обозначим через
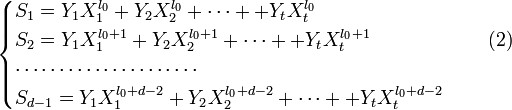
Составим полином локаторов ошибок:
Корнями этого полинома являются элементы, обратные локаторам ошибок. Помножим обе части этого полинома на
Положим
Таким образом для каждого l можно записать свое равенство. Если их просуммировать по l, то получиться равенство, справедливое для каждого
 .
. Учитывая (2) и то, что
(то есть
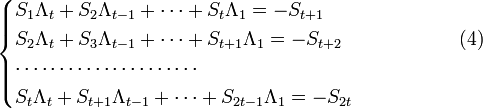
.
Или в матричной форме
Где
![S^{(t)}={ \left[ \begin{matrix}S_1 & S_2 & \dots & S_t \\S_2 & S_3 & \dots & S_{t+1} \\\cdots & \cdots & \cdots & \\S_t & S_{t+1} & \dots & S_{2t-1} \end{matrix} \right] }, \quad \quad \quad \quad \quad\quad(5)](https://bukvasha.net/img/32/dopb313187.zip)
![\bar\Lambda^{(t)} = { \left[ \begin{matrix}\Lambda_t \\\Lambda_{t-1} \\\cdots \\\Lambda_1\end{matrix} \right] }, \quad \quad \bar s^{(t)}{ \left[ \begin{matrix}S_{t+1} \\S_{t+2} \\\cdots \\S_{2t}\end{matrix} \right] }](https://bukvasha.net/img/32/dopb313188.zip)
Если число ошибок и в самом деле равно t, то система (4) разрешима, и можно найти значения коэффициентов
После этого можно решить систему (4) и получить коэффициенты полинома локаторов ошибок. Его корни (элементы, обратные локаторам ошибок) можно найти простым перебором по всем элементам поля GF(qm). К ним найти элементы, обратные по умножению, — это локаторы ошибок
Коды Рида–Соломона
Широко используемым подмножеством кодов БЧХ являются коды Рида-Соломона, которые позволяют исправлять пакеты ошибок. Пакет ошибок длины b представляет собой последовательность из таких b ошибочных символов, что первый и последний из них отличны от нуля. Существуют классы кодов Рида-Соломона, позволяющие исправлять многократные пакеты ошибок.
Коды Рида-Соломона широко используются в устройствах цифровой записи звука, в том числе на компакт-диски. Данные, состоящие из отсчетов объединяются в кадр, представляющий кодовое слово. Кадры разбиваются на блоки по 8 бит. Часть блоков являются контрольными.
Обычно 1 кадр (кодовое слово) = 32 символа данных +24 сигнальных символа +8 контрольных бит = 256 бит.
Сигнальные символы это вспомогательные данные, облегчающие декодирование: служебные сигналы, сигналы синхронизации и т. д.
При передаче данных производится перемежение (изменение порядка следования по длине носителя и во времени) блоков с различным сдвигом во времени, в результате чего расчленяются сдвоенные ошибки, что облегчает их локализацию и коррекцию. При этом используются коды Рида-Соломона с минимальным кодовым расстоянием d0 = 5.
Сверточные кодыКроме рассмотренных корректирующих кодов используются так называемые сверточные коды, контрольные биты, в которых формируются непрерывно из информационных и контрольных бит смежных блоков.
Выводы
Таким образом, в результате написания реферата, пришли к выводу, что коды Боуза-Чоудхури-Хоквингхема – это широкий класс циклических кодов, способных исправлять многократные ошибки.
БЧХ-коды играют заметную роль в теории и практике кодирования. Интерес к ним определяется следующим: коды БЧХ имеют весьма хорошие свойства; данные коды имеют относительно простые методы кодирования и декодирования; коды Рида-Соломона являются широко известным подклассом недвоичных БЧХ кодов, которые обладают оптимальными свойствами, и применяются для исправления многократных пакетов ошибок.
Список использованной литературы
1. Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and practice of error control codes. — М.: Мир, 1986. — С. 576
2. Дмитриев В.И. Прикладная теория информации: Учебник для вузов. М.: Высшая школа , 1989. 320 c.
3. Колесник В.Д., Полтырев Г.Ш. Курс теории информации. – М.: Наука, 1982.
4. Кудряшов Б.Д. Теория информации. Учебник для вузов Изд-во ПИТЕР, 2008. – 320с.
5. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. — М.: Мир, 1976. — С. 596.
6. Семенюк В. В. Экономное кодирование дискретной информации. – СПб.: СПб ГИТМО (ТУ), 2001
7. У. Петерсон, Э. Уэлдон, Коды, исправляющие ошибки, Москва, “Мир”, 1976.
8. Э. Берлекэмп, Алгебраическая теория кодирования, Москва, “Мир”, 1971.